Теплообмен при фазовых превращениях.(капельная конденсация).
Конденсация представляет собой процесс перехода пара (газа) в жидкое или твердое состояние (фазовый переход первого рода).
Конденсация пара на практике: в конденсаторах паровых турбин пар конденсируется на охлаждаемых трубах; конденсация пара осуществляется в опреснительных установках и многочисленных теплообменных аппаратах.
Выделение при фазовом превращении теплоты неразрывно связывает процесс конденсации пара с теплообменом. Процесс конденсации возможен только при докритических состояниях газа (пара) и может быть осуществлен путем его охлаждения или в результате такого сжатия, чтобы при достигнутых значениях температуры и давления конденсированная фаза была термодинамически более устойчивой, чем газообразная. Если при этом температура и давление больше их значений, соответствующих тройной точке для данного вещества, то образуется жидкая конденсированная фаза, если меньше — пар переходит в твердое состояние. Конденсация может происходить как в объеме пара, так и на охлаждаемой поверхности теплообмена. В первом случае образование конденсированной фазы может происходить самопроизвольно при значительном переохлаждении пара относительно температуры насыщения и на холодных жидких или твердых частицах, вводимых в пар.
В энергетике, во многих других областях техники и промышленности чаще приходится иметь дело с конденсацией пара в жидкое состояние на охлаждаемых поверхностях теплообмена. Эта задача прежде всего и будет рассмотрена в данной главе. При этом будем полагать, что конденсирующийся пар не содержит примесей других паров или газов, т. е. является чистым. Конденсация насыщенного или перегретого пара на твердой поверхности теплообмена происходит, если температура поверхности меньше температуры насыщения при данном давлении. На поверхности может образоваться пленка конденсата с толщиной, намного превышающей расстояние эффективного действия межмолекулярных сил. В ряде случаев поверхность тела может быть покрыта отдельными каплями конденсата.
Первый вид конденсации, когда жидкая конденсированная фаза образуется на поверхности теплообмена в виде устойчивой пленки, называется пленочной конденсацией, а второй — когда происходит образование капель — капельной. Пленочная конденсация имеет место, если конденсат смачивает данную поверхность теплообмена. Если же конденсат не смачивает поверхность, то происходит капельная конденсация.
Смачиваемость обычно характеризуют краевым углом q, образованным поверхностью жидкости и поверхностью твердого тела, граничащих с некоторой третьей средой — в данном случае с паром (рис. 12-1).
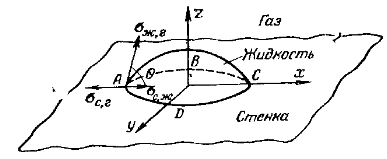 В предположении, что актуальны только капиллярные силы, состояние равновесия капли определяется уравнением
В предположении, что актуальны только капиллярные силы, состояние равновесия капли определяется уравнением 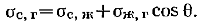
Если sс.г > sс.ж, т. е. если поверхностное натяжение между газом и стенкой больше, чем между твердым телом и жидкостью, краевой угол q< 90°; в этом случае говорят, что жидкость смачивает твердую поверхность. При sс.г < sс.ж краевой угол q> 90°, жидкость не смачивает стенку. Абсолютные смачиваемость и несмачиваемость характеризуются соответственно краевыми углами q=0 и q= 180°.Реально проявляются промежуточные случаи частичного смачивания (q <90°) или частичного несмачивания (q> 90°).Капельная конденсация наблюдается при пуске теплообменного аппарата, когда на поверхностях стенок имеются различные, в том числе и масляные, загрязнения, при конденсации ртутного пара и в некоторых других случаях.Капельная конденсация может быть вызвана с помощью специальных веществ, называемых лиофобизаторами (при конденсации водяного пара — гидрофобизаторами). Эти вещества наносятся па поверхность теплообмена или вводятся в пар.При капельной конденсации водяного пара теплоотдача может быть во много раз больше, чем при пленочной. Это объясняется тем, что пленка конденсата является большим термическим сопротивлением передаче тепла фазового перехода от поверхности конденсации к стенке. При капельной конденсации в силу разрыва пленки это-сопротивление гораздо меньше.В общем случае помимо термического сопротивления конденсата можно выделить дополнительное сопротивление.
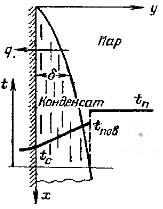 Пологаем: поверхность конденсации плоская (или достаточно близкая к плоской) и толщина слоя конденсата, находящегося па стенке, намного больше радиуса действия межмолекулярных сил (рис. 12-2).
Пологаем: поверхность конденсации плоская (или достаточно близкая к плоской) и толщина слоя конденсата, находящегося па стенке, намного больше радиуса действия межмолекулярных сил (рис. 12-2).
Термическое сопротивление передаче теплоты от пара к стенке можно представить в виде суммы двух слагаемых;
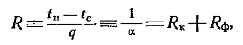 (12.2) где tП и tс - соответственно температуры пара и поверхности стенки; q — плотность теплового потока; a—коэффициент теплоотдачи от пара к стенке.В уравнении (12-2) Rк - термическое сопротивление пленки конденсата. Rф - термическим сопротивлением на границе раздела фаз (межфазным термическим сопротивлением), не является термическим сопротивлением в его обычном понимании. Появление этого сопротивления обусловлено скачком температуры на границе раздела паровой и жидкой фаз.В поверхностном слое пара толщиной порядка средней длины свободного пробега движутся два неравных потока молекул, имеющих различную температуру (энергию). Такой слой называется кнудсеновским. Температура пара в этом слое в среднем отличается от температуры поверхности жидкости. Перепад температур в столь тонком слое в теории сплошных сред воспринимается как скачок. За пределами кнудсеновского слоя из-за соударений молекул температура выравнивается.Чем больше молекул, падающих на жидкость, отражается, не конденсируясь, тем больше скачок температуры. Это учитывается коэффициентом конденсации. Коэффициент конденсации представляет собой отношение числа захватываемых молекул к общему числу молекул пара, ударяющихся о поверхность конденсата. В общем случае коэффициент конденсации может изменяться от нуля до единицы.Поток пара, проходящий через кнудсеновский слой к поверхности жидкости, будет равен
(12.2) где tП и tс - соответственно температуры пара и поверхности стенки; q — плотность теплового потока; a—коэффициент теплоотдачи от пара к стенке.В уравнении (12-2) Rк - термическое сопротивление пленки конденсата. Rф - термическим сопротивлением на границе раздела фаз (межфазным термическим сопротивлением), не является термическим сопротивлением в его обычном понимании. Появление этого сопротивления обусловлено скачком температуры на границе раздела паровой и жидкой фаз.В поверхностном слое пара толщиной порядка средней длины свободного пробега движутся два неравных потока молекул, имеющих различную температуру (энергию). Такой слой называется кнудсеновским. Температура пара в этом слое в среднем отличается от температуры поверхности жидкости. Перепад температур в столь тонком слое в теории сплошных сред воспринимается как скачок. За пределами кнудсеновского слоя из-за соударений молекул температура выравнивается.Чем больше молекул, падающих на жидкость, отражается, не конденсируясь, тем больше скачок температуры. Это учитывается коэффициентом конденсации. Коэффициент конденсации представляет собой отношение числа захватываемых молекул к общему числу молекул пара, ударяющихся о поверхность конденсата. В общем случае коэффициент конденсации может изменяться от нуля до единицы.Поток пара, проходящий через кнудсеновский слой к поверхности жидкости, будет равен 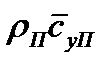 , от жидкости в пар —
, от жидкости в пар — 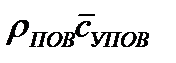 ; здесь
; здесь 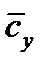 — нормальная к поверхности жидкости составляющая средней скорости молекул. Результирующий поток, отнесенный к единице поверхности, будет
— нормальная к поверхности жидкости составляющая средней скорости молекул. Результирующий поток, отнесенный к единице поверхности, будет 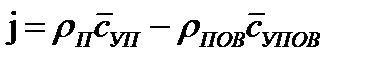 , кг/(м2×с).Из кинетической теории газов следует, что
, кг/(м2×с).Из кинетической теории газов следует, что 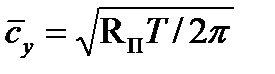 . получим уравнение Герца — Кнудсена:
. получим уравнение Герца — Кнудсена: 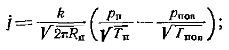 (12.3)здесь Тп и Тпов — соответственно температуры пара и поверхности конденсата; рп. pпов — давление
(12.3)здесь Тп и Тпов — соответственно температуры пара и поверхности конденсата; рп. pпов — давление 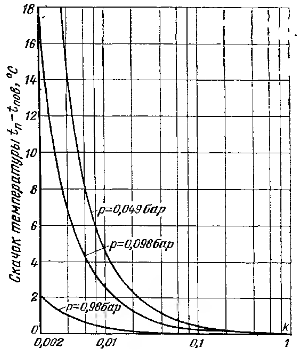 насыщенного пара соответственно при температурах Тп и Тпов; Rп—газовая постоянная пара; k — коэффициент конденсации; rп=рп/ Rп Тп, rпов=рпов/ Rп Тпов.Формула (12-3) получена для сравнительно простой молекулярной модели. Показано, что коэффициент конденсации в этой формуле должен быть заменен функцией k/(1-0,4k).Межфазное термическое сопротивление определяют следующим образом:
насыщенного пара соответственно при температурах Тп и Тпов; Rп—газовая постоянная пара; k — коэффициент конденсации; rп=рп/ Rп Тп, rпов=рпов/ Rп Тпов.Формула (12-3) получена для сравнительно простой молекулярной модели. Показано, что коэффициент конденсации в этой формуле должен быть заменен функцией k/(1-0,4k).Межфазное термическое сопротивление определяют следующим образом: 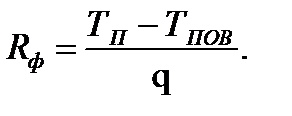 (12.4)Полагая, что переносимая через фазовую границу теплота q есть только теплота фазового перехода, можно написать q=rj где j определяется но уравнению (12-3), r—теплота фазового перехода.На рис. 12-3 приведены значения скачка температуры tп—tпов в зависимости от давления конденсирующегося водяного пара и значения коэффициента конденсации k при q » 29000 Вт/м2. Как следует из графиков, при малом коэффициенте конденсации скачок может быть значительным, особенно при низких давлениях. Из ряда экспериментальных исследований вытекает, что при конденсации чистого водяного пара с давлением примерно р>104 Па с достаточным приближением можно считать, что температурный скачок на границе раздела фаз отсутствует и, как следует из уравнения (12-2)
(12.4)Полагая, что переносимая через фазовую границу теплота q есть только теплота фазового перехода, можно написать q=rj где j определяется но уравнению (12-3), r—теплота фазового перехода.На рис. 12-3 приведены значения скачка температуры tп—tпов в зависимости от давления конденсирующегося водяного пара и значения коэффициента конденсации k при q » 29000 Вт/м2. Как следует из графиков, при малом коэффициенте конденсации скачок может быть значительным, особенно при низких давлениях. Из ряда экспериментальных исследований вытекает, что при конденсации чистого водяного пара с давлением примерно р>104 Па с достаточным приближением можно считать, что температурный скачок на границе раздела фаз отсутствует и, как следует из уравнения (12-2) 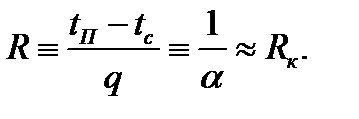 (12.5)Ввиду недостаточности данных о коэффициенте конденсации последнее соотношение часто используют и при расчете конденсации паров других неметаллических жидкостей.Термическое сопротивление пленки конденсата RK зависит от режима течения. Поперек ламинарно текущей пленки теплота переносится теплопроводностью, через турбулентную — дополнительно и конвекцией. Переход от ламинарного течения пленки к турбулентному определяют по величине числа Рейнольдса пленки. Для пленки
(12.5)Ввиду недостаточности данных о коэффициенте конденсации последнее соотношение часто используют и при расчете конденсации паров других неметаллических жидкостей.Термическое сопротивление пленки конденсата RK зависит от режима течения. Поперек ламинарно текущей пленки теплота переносится теплопроводностью, через турбулентную — дополнительно и конвекцией. Переход от ламинарного течения пленки к турбулентному определяют по величине числа Рейнольдса пленки. Для пленки 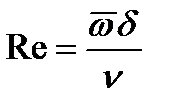 где
где 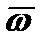 — средняя скорость течения пленки в рассматриваемом поперечном сечении; d — толщина пленки конденсата в этом же сечении; n — кинематический коэффициент вязкости конденсата.Наиболее вероятным значением Reкр для случая конденсации практически неподвижного пара на вертикальной поверхности полагают величину Reкр = 400.Ламинарное течение жидкой пленки может сопровождаться волновым движением — рис. 12-4.
— средняя скорость течения пленки в рассматриваемом поперечном сечении; d — толщина пленки конденсата в этом же сечении; n — кинематический коэффициент вязкости конденсата.Наиболее вероятным значением Reкр для случая конденсации практически неподвижного пара на вертикальной поверхности полагают величину Reкр = 400.Ламинарное течение жидкой пленки может сопровождаться волновым движением — рис. 12-4. 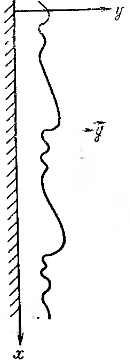 Частицы жидкости, находящиеся на поверхности пленки, под действием случайных возмущений могут получить смещение, приводящее к деформации поверхности и отклонению се от равновесного состояния. При этом возникают силы, стремящиеся вернуть жидкость к равновесию. При стекании пленок большое значение имеет сила, обусловленная поверхностным натяжением жидкости. Под действием восстанавливающих сил жидкие частица стремятся вернуться к положению равновесия. Однако по инерции они будут проходить положение равновесия, вновь испытывать действие восстановительных сил и т. д. На это движение накладывается действие сил тяжести. В результате на поверхности пленки, подвергшейся случайному возмущению, будут возникать волны. Волновые движения, возникающие разновременно в различных местах от случайных возмущений, налагаясь друг на друга, приводят к сложной трехмерной картине процесса. Ламинармо текущая пленка обладает неустойчивостью относительно возмущений с достаточной длиной волны (d). При малых числах Рейнольдса возникающие в слое возмущения сносятся вниз по течению. Если же число Рейнольдса пленки больше некоторого предельного Reволн то образуется устойчивый волновой режим.При периодическом волновом движении пленки, стекающей по вертикальной поверхности под действием сил тяжести,
Частицы жидкости, находящиеся на поверхности пленки, под действием случайных возмущений могут получить смещение, приводящее к деформации поверхности и отклонению се от равновесного состояния. При этом возникают силы, стремящиеся вернуть жидкость к равновесию. При стекании пленок большое значение имеет сила, обусловленная поверхностным натяжением жидкости. Под действием восстанавливающих сил жидкие частица стремятся вернуться к положению равновесия. Однако по инерции они будут проходить положение равновесия, вновь испытывать действие восстановительных сил и т. д. На это движение накладывается действие сил тяжести. В результате на поверхности пленки, подвергшейся случайному возмущению, будут возникать волны. Волновые движения, возникающие разновременно в различных местах от случайных возмущений, налагаясь друг на друга, приводят к сложной трехмерной картине процесса. Ламинармо текущая пленка обладает неустойчивостью относительно возмущений с достаточной длиной волны (d). При малых числах Рейнольдса возникающие в слое возмущения сносятся вниз по течению. Если же число Рейнольдса пленки больше некоторого предельного Reволн то образуется устойчивый волновой режим.При периодическом волновом движении пленки, стекающей по вертикальной поверхности под действием сил тяжести,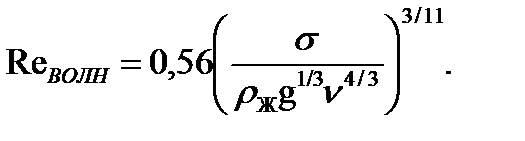 (12.6)Отсюда следует, например, что для воды при t = 15 oC Rеволн » 5. Это значение Rеволн хорошо соответствует результатам, полученным при экспериментальном исследовании.В процессе конденсации расход конденсата тесно связан с тепловым потоком. При конденсации сухого насыщенного пара последним отдается теплота фазового перехода r, Дж/кг. Кроме того, поскольку температура поверхности стенки меньше температуры поверхности конденсата, соприкасающегося с паром, стенке отдается и часть тепла конденсата. Происходит переохлаждение конденсата в среднем до температуры, значение которой лежит между значениями температур поверхностей пленки (со стороны пара) и стенки.Во многих практически важных случаях теплота переохлаждения пренебрежимо мала по сравнению с теплом фазового перехода.В этом случае тепловой поток (или его плотность) не изменяются по толщине пленки конденсата.Пренебрегая теплотой переохлаждения конденсата, можно написать:Q = rG (12.7)где Q — тепловой поток, Вт; G —количество конденсата, образовавшегося в единицу времени, или массовый расход, кг/с.Расход конденсата в каком-либо произвольно выбранном сечении движущейся пленки есть
(12.6)Отсюда следует, например, что для воды при t = 15 oC Rеволн » 5. Это значение Rеволн хорошо соответствует результатам, полученным при экспериментальном исследовании.В процессе конденсации расход конденсата тесно связан с тепловым потоком. При конденсации сухого насыщенного пара последним отдается теплота фазового перехода r, Дж/кг. Кроме того, поскольку температура поверхности стенки меньше температуры поверхности конденсата, соприкасающегося с паром, стенке отдается и часть тепла конденсата. Происходит переохлаждение конденсата в среднем до температуры, значение которой лежит между значениями температур поверхностей пленки (со стороны пара) и стенки.Во многих практически важных случаях теплота переохлаждения пренебрежимо мала по сравнению с теплом фазового перехода.В этом случае тепловой поток (или его плотность) не изменяются по толщине пленки конденсата.Пренебрегая теплотой переохлаждения конденсата, можно написать:Q = rG (12.7)где Q — тепловой поток, Вт; G —количество конденсата, образовавшегося в единицу времени, или массовый расход, кг/с.Расход конденсата в каком-либо произвольно выбранном сечении движущейся пленки есть 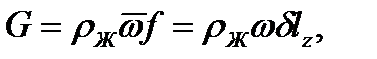 где lz—размер стенки в направлении, нормальном к плоскости чертежа (рис. 12-2). Следовательно,
где lz—размер стенки в направлении, нормальном к плоскости чертежа (рис. 12-2). Следовательно, 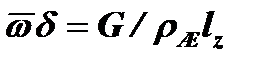 . На участке от 0 до х образовалось G кг/с конденсата и в единицу времени была передана теплота
. На участке от 0 до х образовалось G кг/с конденсата и в единицу времени была передана теплота 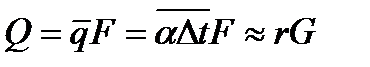 . Отсюда
. Отсюда 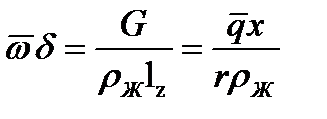 И
И 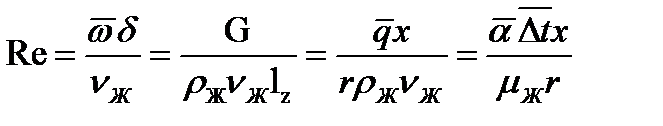 (12.8)Таким образом, при названных условиях число Рейнольдса помимо своей обычной роли гидродинамического критерия является еще и величиной, определяющей интенсивность теплообмена.
(12.8)Таким образом, при названных условиях число Рейнольдса помимо своей обычной роли гидродинамического критерия является еще и величиной, определяющей интенсивность теплообмена.
25. Теплообмен при пленочной конденсации неподвижного пара. Турбулентное течение пленки. А. Вертикальная стенка
Ламинарное течение пленки. На вертикальной стенке, температура поверхности которой всюду равна tc, конденсируется сухой насыщенный пар. Течение пленки имеет ламинарный характер. Будем рассматривать стационарную задачу и полагать, что размер стенки в направлении оси Oz бесконечно велик (рис. 12-2).
Допущения:1- силы инерции, возникающие в пленке конденсата, пренебрежимо малы по сравнению с силами вязкости и силами тяжести;2- конвективный перенос теплоты в пленке, а также теплопроводность вдоль нее не учитываются; учитывается только теплопроводность поперек пленки;3- трение на границе раздела паровой и жидкой фаз отсутствует; температура внешней поверхности пленки конденсата постоянна и равна температуре насыщения tн;4- физические параметры конденсата не зависят от температуры; силы поверхностного натяжения на свободной поверхности пленки не влияют на характер ее течения;5- плотность пара мала по сравнению с плотностью конденсата.
Уравнения движения в проекциях на оси Оу и Oz не учитываем. Пленка движется в направлении оси Ох. Левая часть уравнения движения в проекциях на ось Ох равна нулю, так как задача стационарна и инерционные силы считаются пренебрежимо милыми. В результате получаем систему уравнений
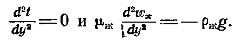 Граничные условия:при у = 0 t = tc и wx=0; при у=d t=tu и дwx/дy = 0.Равенство нулю производной дwx/дy = 0 следует из условия, что трением на границе раздела фаз пренебрегаем. Так как sy=d = 0, а m ¹ 0, то из уравнения s = m(dwx/dy) следует, что при у=d dwx/dy = 0
Граничные условия:при у = 0 t = tc и wx=0; при у=d t=tu и дwx/дy = 0.Равенство нулю производной дwx/дy = 0 следует из условия, что трением на границе раздела фаз пренебрегаем. Так как sy=d = 0, а m ¹ 0, то из уравнения s = m(dwx/dy) следует, что при у=d dwx/dy = 0
Интегрирование уравнения энергии при записанных граничных условиях дает: 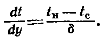 Коэффициент теплоотдачи
Коэффициент теплоотдачи 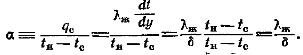
Таким образом, если поперек пленки теплота переносится только теплопроводностью, то 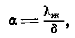 (12.9)т. е. коэффициент теплоотдачи в определенной точке поверхности теплообмена прямо пропорционален коэффициенту теплопроводности и обратно пропорционален толщине пленки конденсата в этой точке.Толщина пленки конденсата будет зависеть от количества образовавшегося конденсата, или расхода конденсата, в интересующем нас сечении. Количество конденсата, протекающего в единицу времени через поперечное сечение пленки при ширине последней, равной единице, определяется следующим выражением:
(12.9)т. е. коэффициент теплоотдачи в определенной точке поверхности теплообмена прямо пропорционален коэффициенту теплопроводности и обратно пропорционален толщине пленки конденсата в этой точке.Толщина пленки конденсата будет зависеть от количества образовавшегося конденсата, или расхода конденсата, в интересующем нас сечении. Количество конденсата, протекающего в единицу времени через поперечное сечение пленки при ширине последней, равной единице, определяется следующим выражением: 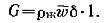 Через сечение, лежащее ниже на величину dx, жидкости протекает больше на
Через сечение, лежащее ниже на величину dx, жидкости протекает больше на 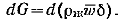 Этот прирост расхода происходит за счет конденсации. Если полагать, что тепло, отданное стенке, есть теплота фазового перехода, будем иметь:
Этот прирост расхода происходит за счет конденсации. Если полагать, что тепло, отданное стенке, есть теплота фазового перехода, будем иметь: 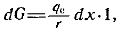 где qс/r — количество конденсата, образующегося на единице поверхности теплообмена за единицу времени. С другой стороны.
где qс/r — количество конденсата, образующегося на единице поверхности теплообмена за единицу времени. С другой стороны. 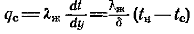 и
и 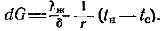 (б)Приравняв правые части уравнений (а) и (б), получим:
(б)Приравняв правые части уравнений (а) и (б), получим:
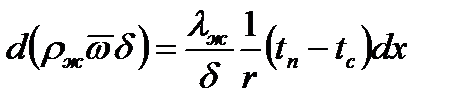 (в) Для того чтобы проинтегрировать последнее уравнение, предварительно нужно определить среднюю скорость
(в) Для того чтобы проинтегрировать последнее уравнение, предварительно нужно определить среднюю скорость 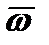 .В уравнении движения d2wx/dy2 = — rжg/m комплекс rжg/m согласно условию является постоянной величиной.R этом случае интегрирование дает:
.В уравнении движения d2wx/dy2 = — rжg/m комплекс rжg/m согласно условию является постоянной величиной.R этом случае интегрирование дает: 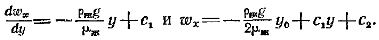 Используя граничные условия, получаем:
Используя граничные условия, получаем: 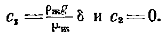 Распределение скоростей тогда будет:
Распределение скоростей тогда будет: 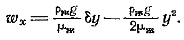 Средняя скорость течениям
Средняя скорость течениям 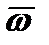 в сечении х равна:
в сечении х равна:
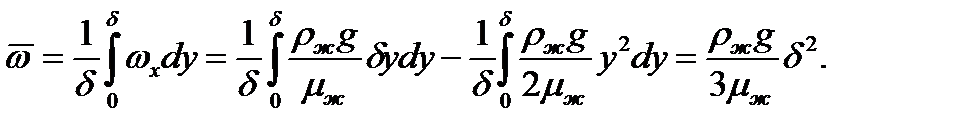 Подстановка полученного значения
Подстановка полученного значения 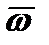 в уравнение (в) даст:
в уравнение (в) даст: 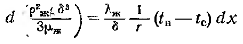 или
или 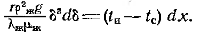 Проинтегрировав это уравнение, получим:
Проинтегрировав это уравнение, получим: 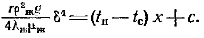 Из условия, что при х = 0 d = 0, следует, что С = 0. Решив последнее уравнение относительно d и учитывая значение постоянной интегрирования, будем иметь, что
Из условия, что при х = 0 d = 0, следует, что С = 0. Решив последнее уравнение относительно d и учитывая значение постоянной интегрирования, будем иметь, что 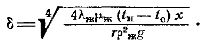
Подставив значение d в выражение a=lж/d, получим следующее уравнение для местного коэффициента теплоотдачи:  (12.12)В рассматриваемой задаче температурный напор Dt = tв—tc не изменяется по х. В этом случае методы осреднения коэффициента теплоотдачи дают одинаковые результаты. Получаем, что
(12.12)В рассматриваемой задаче температурный напор Dt = tв—tc не изменяется по х. В этом случае методы осреднения коэффициента теплоотдачи дают одинаковые результаты. Получаем, что 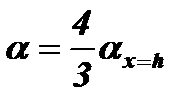 и, следовательно,
и, следовательно, 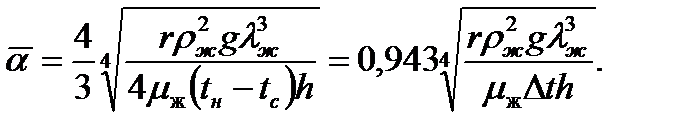 (12.13)
(12.13)
где h – высота стенки Уравнение (12.13) – уравнение Нуссельта.
Переменность температуры поверхности вертикальной стенки не влияет на среднюю теплоотдачу, если коэффициент теплоотдачи вычисляется по уравнению 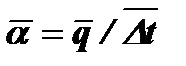 .Из уравнений (12-11) — (12-13) следует, что
.Из уравнений (12-11) — (12-13) следует, что 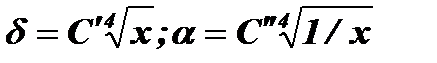 и
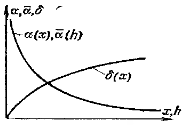
и 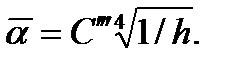 Характер зависимостей изображен на рис. 12-5. Коэффициенты теплоотдачи уменьшаются с увеличением х или h, а толщина пленки, наоборот, увеличивается. Увеличением толщины пленки объясняется уменьшение коэффициентов теплоотдачи, так как термическое сопротивление при этом увеличивается.
Характер зависимостей изображен на рис. 12-5. Коэффициенты теплоотдачи уменьшаются с увеличением х или h, а толщина пленки, наоборот, увеличивается. Увеличением толщины пленки объясняется уменьшение коэффициентов теплоотдачи, так как термическое сопротивление при этом увеличивается.
 Согласно закону Ньютона—Рихмана qс=aDt и в то же время a=сDt 3/4. Таким образом, в рассматриваемом случае
Согласно закону Ньютона—Рихмана qс=aDt и в то же время a=сDt 3/4. Таким образом, в рассматриваемом случае 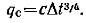
Вследствие принятых допущений решение Нуссельта следует рассматривать как приближенное.
Пленка имеет сложный волновой характер движения, зависящий от числа Re и других факторов. Поправка на волновое течение с достаточной точностью есть функция только числа Рейнольдса:ev = Re0,04
При малых Re поправка ev; близка к единице. По мере увеличения Re величина ev возрастает и при Re=400 ev = 1,27. Число Рейнольдса относится к нижнему по ходу движения конденсата сечению пленки.Таким образом, для расчета средних коэффициентов теплоотдачи при конденсации практически неподвижного чистого пара па вертикальных поверхностях может быть использована формула
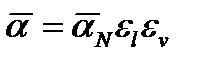 (12.14)
(12.14) 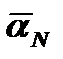 — коэффициент теплоотдачи, вычисляемый по формуле Нуссельта (12-13) при отнесении всех физических параметров конденсата к температуре насыщения.Уравнение Нуссельта (12-13) и уравнение (12-14) могут быть приведены к безразмерному виду:
— коэффициент теплоотдачи, вычисляемый по формуле Нуссельта (12-13) при отнесении всех физических параметров конденсата к температуре насыщения.Уравнение Нуссельта (12-13) и уравнение (12-14) могут быть приведены к безразмерному виду: 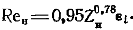
где 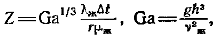 Индекс «ж» показывает, что физические параметры конденсата, входящие в числа Re и Z, выбираются по температуре насыщения. Поправка ev входит в уравнение (12-15) в неявном виде.
Индекс «ж» показывает, что физические параметры конденсата, входящие в числа Re и Z, выбираются по температуре насыщения. Поправка ev входит в уравнение (12-15) в неявном виде.
Если задана плотность теплового потока 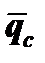 , то формулу (12-14) удобнее использовать в преобразованном виде. Из уравнений a=lж/d и
, то формулу (12-14) удобнее использовать в преобразованном виде. Из уравнений a=lж/d и 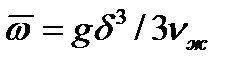 приняв ev = 1,21, можно получить:
приняв ev = 1,21, можно получить: 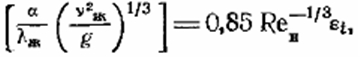
где 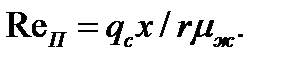 Здесь средняя плотность теплового потока
Здесь средняя плотность теплового потока 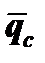 зависит от х.
зависит от х.
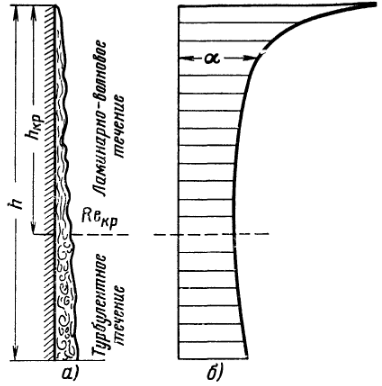
Турбулентное течение пленки. При Rе³400 течение в пленке становится турбулентным. В верхней же части пленки, где Re<400, течение продолжает оставаться ламинарным. На стенке будет иметь место смешанное течение конденсата. Без учета теплоты переохлаждения, диссипации механической энергии и при отсутствии в жидкости внутренних источников теплоты перенос тепла через пленку конденсата происходит в условиях постоянной плотности теплового потока поперек пленки, т. е
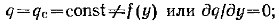 (12.16)
(12.16)
Здесь y — координата, нормальная к поверхности стенки (рис. 12-2). Локальный коэффициент теплоотдачи при пленочной конденсации может быть найден на основе уравнений (а) и
| Характер течения конденсатной пленки (а)и изменение коэффициента теплоотдачи (б) вдоль вертикальной плиты большой высоты. При hкр течение в пленке приобретает турбулентный характер. |
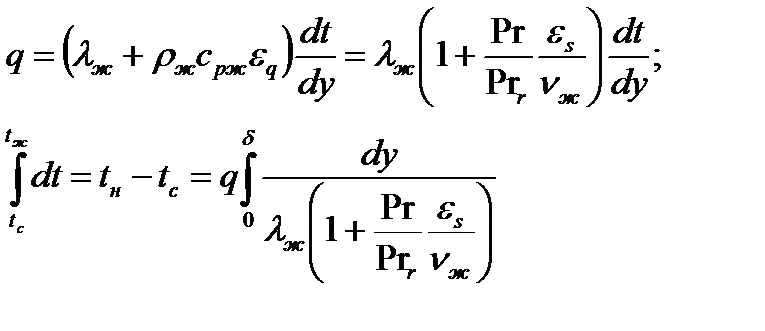
отсюда, учитывая, что a = qc/(tн—tc), получаем:
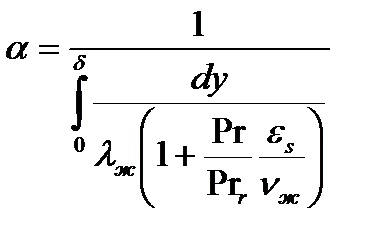 (12.17)Таким образом, определение коэффициента теплоотдачи сводится к вычислению интеграла, стоящего в знаменателе уравнения (12-17). Было принято, что физические параметры конденсата постоянны и eq = es (т. е. Рrт=1). Результаты интегрирования аппроксимированы в интервалах 1 £ Рrж £ 25 и 1,5×103 £ Rе £ 6,9×104 уравнением
(12.17)Таким образом, определение коэффициента теплоотдачи сводится к вычислению интеграла, стоящего в знаменателе уравнения (12-17). Было принято, что физические параметры конденсата постоянны и eq = es (т. е. Рrт=1). Результаты интегрирования аппроксимированы в интервалах 1 £ Рrж £ 25 и 1,5×103 £ Rе £ 6,9×104 уравнением
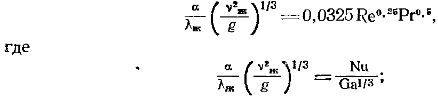 (12.18)
(12.18)
здесь a — местный коэффициент теплоотдачи.При расчете средней теплоотдачи турбулентного течения нужно учесть, что в верхней части стенки на ламинарном участке уже образовался определенный слой конденсата.В случае постоянных физических параметров теплоотдача ламинарного участка описывается уравнением (12-15), где et = 1:Re = 0,95 Z0,78 .При этом величине ReKР=400 соответствует 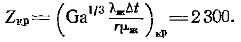 Полагая ReKР=400, ZKР = 2300, получаем следующее уравнение:
Полагая ReKР=400, ZKР = 2300, получаем следующее уравнение: 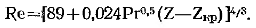 (12.19)
(12.19)
Уравнение (12-19) описывает среднюю теплоотдачу для вертикальной поверхности, на которой имеются ламинарный и турбулентный участки течения конденсата.Для учета зависимости физических параметров от температуры коэффициент 0,0325 в формуле (12-18) или коэффициент 0,024 в формуле (12-19) должен быть умножен на поправку (Prн/Рrс)0,25, где индексы «н» и «с» означают, что число Прандтля конденсата выбирается соответственно по температурам насыщения и стенки. При этом все остальные физические параметры конденсата, входящие в уравнения (12-18) и (12-19), должны выбираться по температуре насыщения.С учетом сделанных замечаний формула для расчета среднего коэффициента теплоотдачи при конденсации чистого неподвижного пара на вертикальной поверхности и смешанном течении пленки конденсата принимает следующий вид: 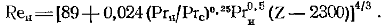 (12.20)
(12.20)
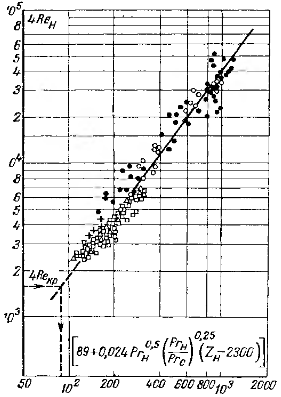
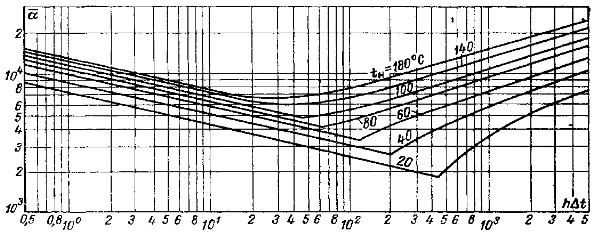
| Рис 12-7 Теплоотдача при пленочной конденсации неподвижного пара на вертикальной поверхности при смешанном (ламинарном и турбулентном) течении пленки конденсата |
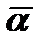 , если известны высота h поверхности теплообмена, температурный напор Dt = tн—tc и температура насыщения пара. Рис. 12-8 График для расчета среднего коэффициента теплоотдачи при пленочной конденсации неподвижного пара на вертикальной поверхности.
, если известны высота h поверхности теплообмена, температурный напор Dt = tн—tc и температура насыщения пара. Рис. 12-8 График для расчета среднего коэффициента теплоотдачи при пленочной конденсации неподвижного пара на вертикальной поверхности.
Б. Горизонтальная труба
В случае наклонной стенки в исходное уравнение движения вместо g необходимо ввести проекцию вектора ускорения силы тяжести на ось Ох: 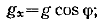
здесь j — угол, образованный направлением силы тяжести и осью координат Ох; ось Ох ориентирована по ходу течения пленки.В результате для наклонных стенок получается следующая формула: 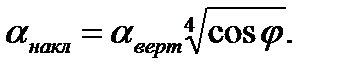 Для криволинейном поверхности, в частности для горизонтального цилиндра, угол j будет переменной величиной. Учитывая это и принимая, что d < d, где d — диаметр круглого цилиндра, Нуссельт получил следующую формулу для расчета среднюю по наружной окружности трубы коэффициента теплоотдачи при условии ламинарного течения пленки конденсата:
Для криволинейном поверхности, в частности для горизонтального цилиндра, угол j будет переменной величиной. Учитывая это и принимая, что d < d, где d — диаметр круглого цилиндра, Нуссельт получил следующую формулу для расчета среднюю по наружной окружности трубы коэффициента теплоотдачи при условии ламинарного течения пленки конденсата: 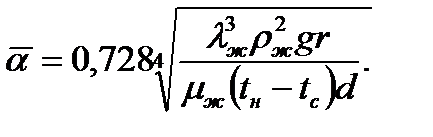 (12.21)Формула (12-21) отличается от формулы (12-13) для вертикальной стенки тем, что коэффициент пропорциональности вместо 0,943 равен 0,728 и в качестве характерного размера вместо h вводится d.
(12.21)Формула (12-21) отличается от формулы (12-13) для вертикальной стенки тем, что коэффициент пропорциональности вместо 0,943 равен 0,728 и в качестве характерного размера вместо h вводится d.
Формула (12-21) получена при условии tc=const. При qc=const коэффициент пропорциональности, равный 0,728, должен быть заменен па 0,693.
Дата добавления: 2021-06-28; просмотров: 1063;











