Теплоотдача при капельной конденсации в трубах.(вертикальный и горизонтальных).

Капельная конденсация имеет место, если конденсат не смачивает поверхность теплообмена. В этом случае поверхность покрыта отдельными каплями. Капельная конденсация, строго говоря, является нестационарным процессом. Однако, если осредненные во времени характеристики процесса не изменяются, то такой процесс можно рассматривать 'как стационарный.

При первичном соприкосновении пара с оголенной поверхностью стенки образуется адсорбционный слой; быстро идущий процесс конденсации приводит к образованию полимолекулярной жидкой пленки.

Пока пленка очень тонка, она находится в силовом молекулярном поле смежных фаз (твердой стенки и пара), в результате чего приобретает особые свойства, отличные от свойств этой же жидкости в боль­шом объеме (вдали от границы раздела фаз). Такую пленку будем называть тонкой. Тонкая пленка находится под избыточным давлением, которое называется расклинивающим. Расклинивающее давление обратно пропорционально примерно кубу толщины пленки: 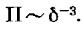При несмачивании действие расклинивающего давления проявляется в том, что поверхности тонкой пленки притягиваются друг к другу, причем тем в большей степени, чем тоньше пленка. Такому расклинивающему давлению приписывают знак минус. Локальное утонение пленки (например, на выступе стенки, в результате местных дефектов структуры твердого тела, изменения лиофобности, меньшей местной скорости конденсации и т. п.) приводит к увеличению расклинивающего давления в этом месте по сравнению с соседними. В результате жидкость быстро вытесняется на смежные участки, где и образуются пер­вичные капли, размеры которых больше эффективного радиуса действия межмолекулярных сил.При положительном расклинивающем давлении («отталкивании поверхностей» тонкой пленки) имеет место пленочная конденсация (образуется толстая пленка); говорят, что поверхность тела смачивается данной жидкостью.Поскольку при интенсивной капельной конденсации акты образования первичных капель непрерывно происходят на оголившейся поверхности стенки, можно полагать, что в среднем на стенке существует тонкая и толстая (капли) пленка. Одновременное существование тонкой пленки и видимых капель следует представлять только в динамике.Известно, что равновесное давление насыщенного пара над выпуклой поверхностью раздела фаз больше, чем над плоской. Конденсация пара на сферической капле с радиусом R, взвешенной в паре, может происходить только при условии, что R>R_K, где R_K — критический (минимально возможный) радиус кривизны поверхности раздела фаз. В случае тонкой сферической пленки необходимо учитывать и влияние ее толщины.

Разность давлений в тонком сферическом слое конденсата и в паре при учете капиллярных эффектов первого и второго рода может быть описана уравнением

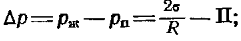(12.36)здесь s — коэффициент поверхностного натяжения на границе жидкость— пар; R — радиус слоя.Соответственно критическое переохлаждение пара DT_к в случае сферических пленок описывается уравнением

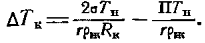(12.37)Первый член правой части уравнения учитывает капиллярные эффекты первого рода (поверхностное натяжение), второй — расклинивающее давление. Если существующее переохлаждение пара DT больше расчетного DT_к, конденсация термодинамически возможна (здесь DT =Т_Н — Т_П0В, где Т_Н и Т_П0В — соответственно абсолютные температуры насыщенного пара при заданном давлении и температура слоя жидкости). Если DT <DT_к, должно происходить испарение слоя, т. е. термодинамически возникновение такого слоя нереально. При DT =DT_к имеет место равновесное состояние системы.В случае П®0 уравнения (12-36) и (12-37) переходят в известные уравнения Лапласа и Томсона: 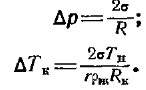(12.38) (12.39)Как следует из уравнения (12-37), требуемое переохлаждение на­сыщенного пара над тонкой несмачивающей пленкой (П < 0) будет больше, чем переохлаждение над сферической поверхностью крупной капли. Из формулы (12-37) также следует, что при конденсации во впадинах стенки (R<0) требуемое переохлаждение меньше, чем при конденсации на выступах (R>0). В результате при прочих равных условиях наиболее вероятными местами образования конденсированной фазы являются микровпадины тела. В реальных условиях поверхность твердого тела не является абсо­лютно однородной, в частности гладкой. Чем больше температурный напор t_Н — t_C, тем больше микронеровностей способны являться центрами зародышеобразования (центрами конденсации), количество первичных капель увеличивается.Критическое переохлаждение DT_к зависит также от физических свойств сред, участвующих в теплообмене. В частности, эта зависимость проявляется и для расклинивающего давления.При конденсации паров органических жидкостей требуемая величина переохлаждения DT_к обычно мала. Требуемое переохлаждение для ртутного пара очень велико. Промежуточное положение занимает конденсация водяного пара. При капельной конденсации жидкая фаза находится в своеобразном движении. В общем случае на поверхности стенки в каждый момент времени существует множество капель, радиус которых изменяется от критического R_к до отрывного R_o. Спектр размеров капель может быть описан дифференциальной функцией распределения капель по размерам j(R)=dn/dR_, м ³, где dn — число капель с радиусом от R до R+dR_, приходящееся на единицу поверхности стенки.Если процесс капельной конденсации является квазистационарным, j(R) = const. Непрерывное увеличение размеров капель за счет конденсации и слияний компенсируется возникновением новых (первичных) и исчезновением крупных (достигших отрывного размера).Приращение объема капли в единицу времени за счет конденсации определяется уравнением 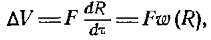где F — поверхность капли, обращенная в пар; w(R)=dR/dt_, м/с — функция скорости роста капли.При этом выделяется теплота фазового перехода.Будем считать каплю полусферой. Для капель с радиусами от R до R+dR выделенная теплота фазового перехода, отнесенная к единице поверхности стенки и к единице времени, определяется уравнением 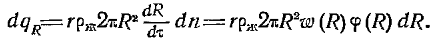Тогда средняя плотность теплового потока будет; 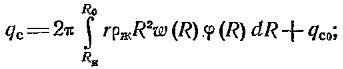(12.40)здесь .член q_с0 учитывает теплоту, выделившуюся при образовании первичных капель. Обычно эта теплота пренебрежимо мала. Температурные напоры при капельной конденсации обычно также невелики, что позволяет не учитывать и теплоту переохлаждения капель относительно t_Н.Таким образом, для теоретического расчета q_с или a= q_с /Dt необходимо знать функции роста капель w(R) и распределения по размерам j(R). Эти функции ищутся для различных условий как аналитически, так и экспериментально. Например, согласно' опытным данным и расчетам скорость роста полусферической капли, когда основным термическим сопротивлением является термическое сопротивление теплопроводности капли, определяется уравнением 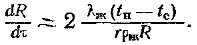Помимо описанного подхода для определения коэффициентов теплоотдачи используется непосредственный эксперимент.Средний коэффициент теплоотдачи при капельной конденсации неподвижного пара может быть описан следующими уравнениями:

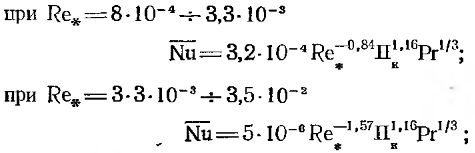(12.41)

здесь 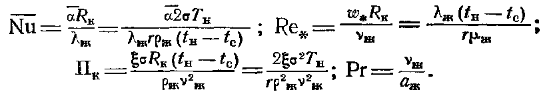(12.42)

Физические параметры конденсата в формулах (12-41) и (12-42) выбираются по температуре насыщения t_Н.Масштабами линейных размеров и скорости являются критический радиус R_K, определяемый формулой (12-39), и условная скорость роста конденсированной фазы при отводе тепла фазового перехода теплопроводностью 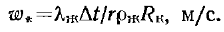Безразмерное число П_кучитывает влияние капиллярных сил. Входящая в него величина x(t_Н—t_c) отражает зависимость поверхностного натяжения от температуры. Здесь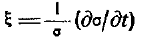

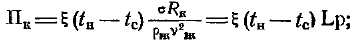— температурный коэффициент поверхностного натяжения. В результате число П_к можно трактовать как отношение термокапиллярных сил к силам вязкости. Его можно представить следующим образом: 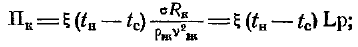здесь Lp = sR_к/r_жn²_ж — число Лапласа

На рис. 12-13 формулы (12-41) и (12-42) сопоставлены с опытными данными. Опытные данные получены при конденсации насыщенного водяного пара на вертикальных стенках высотой до 0,61 м вертикальных трубках и горизонтальном пучке труб. Значения критерия П_кв использованных опытных данных изменялись от 0,98×10^-2 до 4,5×10^-2, число Прандтля изменялось от 1,75 до 3,65; давление пара p_П » (0,12¸1) 10⁵ Па.

Как следует из формул (12-41) и (12-42), для расчета коэффициента теплоотдачи достаточно знать температуру насыщения и температурный напор. На рис. 12-14 представлена номограмма, с помощью ко­торой можно определить коэффициент теплоотдачи при капельной кон­денсации неподвижного насыщенного водяного пара. Номограмма получена путем соответствующего пересчета и графического представ­ления формул (12-41) и (12-42). Согласно формулам (12-41) и (12-42)

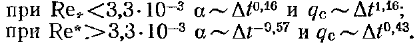Из последних соотношений и из рис. 12-14 следует, что при малых температурньтх напорах коэффициент теплоотдачи возрастает по мере увеличения Dt, а при больших Dt, наоборот, уменьшается. Переход от положительной зависимости a(Dt) к отрицательной происходит при Re_*, равном примерно 3,3×10^-3.

Изменение характера зависимости a(Dt) можно объяснить следующим образом. При Re_*<33,3×10^-3 скорость конденсации лимитируется прежде всего необходимостью пересыщения пара. Чем больше Л/, тем больше пересыщение пара и тем интенсивнее происходит конденсация. При этом термическое сопротивление конденсата сравнительно невелико. Повышение скорости конденсации с ростом Dt и увеличение количества конденсированной фазы на поверхности теплообмена приводят к тому, что термическое сопротивление конденсата начинает оказывать большее влияние на процесс теплоотдачи.При Re_* > 33,3×10^-3 скорость конденсации прежде всего зависит от термического сопротивления образовавшегося конденсата. Происходит своеобразный кризис капельной конденсации.

Теплоотдача при капельной конденсации начинает зависеть от скорости пара при сравнительно небольшой ее величине.В то же время, интенсифицирующее влияние скорости пара, приводящее к появлению большого количества конденсата на поверхности стенки, может ускорить кризис капельной конденсации.

На рис. 12-15 показана зависимость средних коэффициентов теплоотдачи от скорости пара. Водяной пар атмосферного давления конденсировался на вертикальной пластине, протекая вдоль нее сверху вниз. На графике 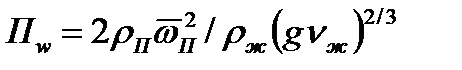; 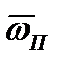— средняя скорость пара на расчетном участке; a_о — коэффициент теплоотдачи, рассчитанный по формуле (12-41).

Рис. 12-15. Зависимость теплоотдачи при капельной конденсации от скорости пара.

Опытные данные, представленные на рис. 12-15, получены при Re_*= 8×10^-4¸3, ×10^-3. Они могут быть описаны уравнением

(12.43)

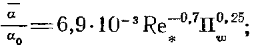
здесь определяющей является температура насыщения.Из формулы (12-43) следует, что 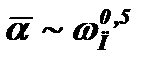и 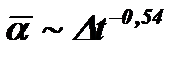. Согласно опытам, данные которых представлены на рис. 12-15, 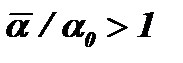. Максимальное увеличение теплоотдачи составляло 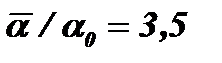( 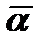= 425×10³ Вт/(м²×К) и имело место при Dt=1К и 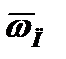=6,6 м/с. Интенсифицирующее воздействие скорости пара проявляется и при Re_*>3,3×10^-3. Однако при значительных температурных напорах средний коэффициент теплоотдачи при конденсации движущегося пара мало отличается от a₀.Опыты показывают, что при капельной конденсации стенание конденсата с верхней трубки на трубку, лежащую под ней, приводит к незначительному уменьшению коэффициента теплоотдачи. Теплоотдача понижается примерно на 10—15%.Интенсивность теплоотдачи при капельной конденсации очень сильно зависит от примеси неконденсирующихся газов. Рассмотренные расчетные соотношения справедливы при конденсации чистого насыщенного пара и на чистой поверхности. Поэтому при определении значения коэффициента теплоотдачи по возможности необходимо учитывать ряд дополнительных обстоятельств, влияющих на теплоотдачу.а. Влияние перегрева пара. Если температура стенки ниже температуры насыщения, то процесс конденсации пе­регретого пара протекает так же, как и насыщенного. Конечно, это не значит, что перегретый пар сразу становится насыщенным во всем объеме; насыщенным пар становится лишь у стенки по мере его охлаждения, а вдали от стенки он может и будет оставаться перегретым. При конденсации перегретого пара необходимо учитывать теплоту перегрева 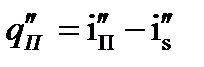, Дж/кг, и вместо теплоты фазового перехода r в расчетную формулу подставлять значение r' = r + q''_П,где 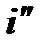и 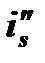— энтальпии перегретого и насыщенного пара соответственно. За разность температур при этом по-прежнему принимается Dt = t_s—t_c.Так как r' > r, то при конденсации перегретого пара теплоотдача несколько выше, чем при конденсации насыщенного пара. Однако разница обычно незначительна и в практических расчетах ею часто вполне можно пренебречь.б. Влияние состояния поверхности. Теплоотдача при конденсации пара зависит от состояния поверхности. Если поверхность шероховата или покрыта слоем окисла, то вследствие дополнительного сопротивления течению толщина пленки увеличивается, а коэффициент теплоотдачи при этом снижается. Здесь большое влияние оказывает также термическое сопротивление окисной пленки на поверхности.в. Влияние содержания в паре неконденсирующихся газов. При наличии в паре воздуха или других неконденсирующихся газов теплоотдача при конденсации сильно снижается. Это происходит потому, что на холодной стенке конденсируется только пар, а воздух остается. При отсутствии конвекции с течением времени воздух скапливается около стенки и оказывает значительное препятствие продвижению пара к стенке.

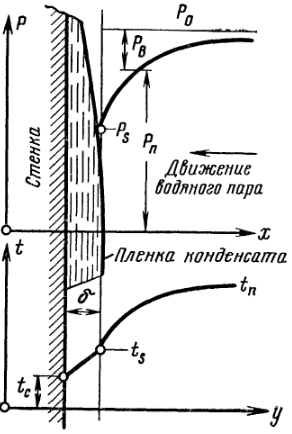В самом деле, на основании закона Дальтона общее давление смеси р₀ составляется из парциальных давлений пара р_П и воздуха р_в, т. е. р₀ = р_П + р_в. Вследствие конденсации пара р_П у стенки меньше, чем в остальном объеме. Поэтому в направлении к стенке р_П непрерывно падает, и чем ближе к стенке, тем быстрее, а р_в, наоборот, возрастает (рис. 4-32). Следовательно, у стенки получается зона с повышенным содержанием воздуха, через которую молекулы пара проникают лишь путем диффузии. Следствием этого является снижение температурного напора, t_s—i_c, так как из-за уменьшения парциального давления пара у поверхности пленки температура насыщения t_s всегда ниже температуры насыщения при давлении р₀.

Опытная кривая изменения относительного коэффициента теплоотдачи в зависимости от концентрации воздуха в паре приведена на рис. 4-33. Здесь по оси абсцисс нанесено значение массовой концентрации воздуха в паре À = т_В/т_П, %, а по оси ординат — отношение a_в/a, где т_В — масса воздуха, кг; т_П — масса пара, кг, содержащиеся в единице объема смеси. Коэффициент теплоотдачи a_в отнесен к разности температур t_П—t_C, где t_П — температура паровоздушной смеси вдали от поверхности, °С. Опыты проводились на горизонтальных трубах.

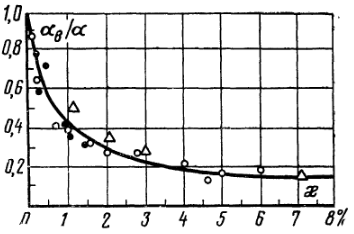Как видно из рисунка, при содержании в паре даже 1% воздуха коэффициент теплоотдачи снижается на 60%. При работе промышленных конденсаторов воздух непрерывно отсасывается, хотя здесь вследствие хорошего перемешивания наличие воздуха сказывается меньше.г. Влияние скорости и направления течения пара. Приведенные выше зависимости справедливы для неподвижного пара или когда скорость его течения мала. При значительных скоростях поток пара оказывает динамическое воздействие на конденсатную пленку. Если движение пара совпадает с направлением течения пленки, поток пара ускоряет движение конденсата в пленке, ее толщина уменьшается, и коэффициент теплоотдачи возрастает. При движении пара снизу вверх, т. е. в обратном направлении, течение пленки тормозится, толщина ее увеличивается, а коэффициент теплоотдачи уменьшается. Однако такое явление происходит лишь до тех пор, пока динамическое воздействие пара не превысит силу тяжести. После этого пленка пара увлекается вверх и частично срывается с поверхности. При этом с увеличением скорости пара коэффициент теплоотдачи вновь растет.

д. Влияние компоновки поверхности нагрева. При проектировании конденсационных устройств большое внимание должно уделяться правильной компоновке поверхности нагрева. Теплоотдача на горизонтальных трубах имеет большую интенсивность, чем на вертикальных, так как в первом случае толщина пленки конденсата меньше. Однако это справедливо лишь для одной трубки или для верхнего ряда в пучке. В многорядных пучках конденсат с верхних рядов стекает на нижние, поэтому и пленка здесь получается более толстой. Однако в реальных условиях конденсат стекает в виде отдельных капель или струйками, что вызывает одновременно значительные возмущения и даже турбулизацию пленки. Кроме того, при конденсации пара на многорядном пучке необходимо учитывать влияние скорости движения поступающего пара в зазорах между трубами, которая может из­менять характер стекания конденсата.

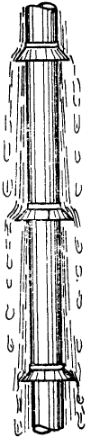Для вертикальных труб коэффициент теплоотдачи книзу уменьшается вследствие утолщения пленки. В этом случае среднее значение теплоотдачи можно увеличить путем установки по высоте трубы конденсатоотводных колпачков (рис. 4-34). Установка таких колпачков через каждые 10 см на трубе высотой h = 3 м увеличивает среднее значение коэффициента теплоотдачи в 2—3 раза.

Еще большее увеличение теплоотдачи получается при подаче пара в виде тонких струек, движущихся с большой скоростью. При ударе таких струек о стенку происходит разрушение пленки и разбрызгивание конденсата. По опытным данным термическое сопротивление теплоотдачи при этом уменьш. в 3-10 раз.

3. Теплоотдача при конденсации пара в трубах. Если в трубу с охлаждаемой поверхностью подводится пар, то по мере прохождения по трубе пар постепенно конденсируется и на стенках обра­зуется пленка конденсата. При этом расход пара G" и его скорость w" падают по длине трубы, а расход конденсата G'увеличивается. Основной особенностью процесса конденсации в трубах является наличие динамического взаимодействия между паровым потоком и пленкой. На пленку конденсата действует также сила тяжести. В итоге в зависимости от ориентации трубы в пространстве и скорости пара характер движения конденсата может быть различным.

В вертикальных трубах при движении пара сверху вниз силы тяжести и динамического воздействия парового потока совпадают по направлению и пленка конденсата стекает вниз. В коротких трубах при небольшой скорости парового потока течение пленки в основном определяется силой тяжести аналогично случаю конденсации неподвижного пара на вертикальной стенке. Такой же оказывается и интенсивность теплоотдачи. При увеличении скорости пара интенсивность теплоотдачи растет. Это объясняется уменьшением толщины конденсатной пленки, которая под воздействием парового потока течет быстрее. В длинных трубах при больших скоростях движения пара картина процесса усложняется. В этих условиях наблюдаются частичный срыв жидкости с поверхности пленки и образование парожидкостной смеси в ядре потока. При этом влияние силы тяжести постепенно утрачивается, и закономерности процесса перестают зависеть от ориентации трубы в пространстве.

В горизонтальных трубах при не очень больших скоростях парового потока взаимодействие сил тяжести и трения пара о пленку приводит к иной картине течения. Под влиянием силы тяжести пленка конденсата стекает по внутренней поверхности трубы вниз. Здесь конденсат накапливается и образует ручей. На это движение накладывается движение конденсата в продольном направлении под воздействием парового потока. В итоге интенсивность теплоотдачи оказывается переменной по окружности трубы: в верхней части более высокая, чем в нижней. Из-за затопления нижней части сечения горизонтальной трубы конденсатом средняя интенсивность теплоотдачи при небольших скоростях пара может оказываться даже более низкой, чем при конденсации неподвижного пара снаружи горизонтальной трубы того же диаметра.

При конденсации в трубах различают режимы полной и частичной конденсации пара. В первом случае весь поступающий в трубу пар конденсируется целиком, и на выходе из трубы движется сплошной поток конденсата. При частичной конденсации на выходе из трубы течет парожидкостная смесь.

Поскольку полный расход пара и конденсата G по длине трубы не изменяется, уравнение материального баланса для любого поперечного сечения трубы имеет вид:G" + G' = G= const.Отношение расхода пара G", проходящего через данное сечение трубы, к полному расходу G называют расходным массовым паросодержанием двухфазного потока в этом сечении; его принято обозначать символом х: х = G"/G.Так, если на вход в трубу поступает насыщенный пар, то во входном сечении расходное массовое паросодержание равно единице (х₁ = 1). При подаче в трубу влажного пара расходное массовое паросодержание на входе меньше единицы (х₁ < 1). По мере движения потока по трубе вследствие конденсации содержание пара уменьшается. При полной конденсации пара в выходном сечении х₂ = 0, при частичной х₂>0.

Теплообмен при кипении однокомпонентных жидкостей. Механизм процесса теплообмена при пузырьковом кипении. Ур-ие равновесия сил для парового пузырька. Работа образования пузырьков. Скорость их роста. Отрывной диаметр.

Кипением называется процесс интенсивного парообразования, происходящего во всем объеме жидкости, находящейся при температуре насыщения или несколько перегретой относительно температуры насыщения, с образованием паровых пузырей. Процесс кипения обычно связан с подводом теплоты к кипящей жидкости. Различают кипение жидкости на твердой поверхности теплообмена, к которой извне подводится теплота, и кипение в объеме жидкости.
При кипении на твердой поверхности образование паровой фазы наблюдается в отдельных местах этой поверхности. При объемном кипении паровая фаза возникает самопроизвольно (спонтанно) непосредственно в объеме жидкости в виде отдельных пузырьков пара. Объемное кипение может происходить лишь при более значительном перегреве жидкой фазы относительно температуры насыщения при данном давлении, чем кипение на твердой поверхности. Значительный перегрев может быть получен, например, при быстром сбросе давления в системе. Объемное кипение может иметь место при наличии в жидкости внутренних источников тепла. По мере увеличения температуры поверхности нагрева и соответственно температурного напора число действующих центров парообразования растет, процесс кипения становится все более интенсивным. Паровые пузырьки периодически отрываются от поверхности и, всплывая к свободной поверхности, продолжают расти в объеме. Последнее объясняется тем, что температура в объеме кипящей жидкости, как показывают опытные данные, не равна температуре насыщения, а несколько превышает се. При повышении температурного напора значительно возрастает поток теплоты, который отводится от поверхности нагрева к кипящей жидкости, вся эта теплота в конечном счете расходуется на образование пара.

Поэтому уравнение теплового баланса при кипении имеет вид:

Q = r×G,

где Q— тепловой поток, Вт; r— теплота фазового перехода жидкости, Дж/кг; G— количество пара, образующегося в единицу времени в результате кипения жидкости и отводимого от ее свободной поверхности, кг/с.

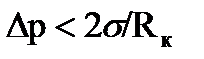
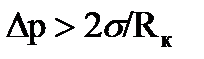
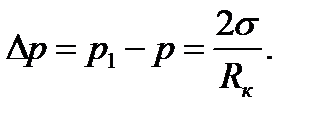Процесс парообразования можно разбить на отдельные стадии. К первоначальной стадии относится зарождение пузырьков в некоторых центрах на поверхности нагрева. Затем происходит их рост и отрыв от этих центров. К завершающей стадии относится движение пузырьков в объеме перeгpетой жидкости. Достигнув поверхности жидкости, паровые пузырьки лопаются. После этого образуются новые пузырьки, и процесс повторяет-ся вновь. Минимальный размер парового пузырька в момент зарождения называется критическим радиусом (R_K). Он соответствует размеру неровностей на поверхности теплообмена (центров парообразования). При наличии центров паровые пузырьки возникают при незначительных перегревах жидкости относительно температуры насыщения. Критический радиус определяется из условий термодинамического равновесия фаз. Для возникновения парового пузырька и существования его в дальнейшем необходимо, чтобы сила давления пара внутри него была не меньше суммы всех внешних сил, действующих на паровой пузырек. В момент образования пузырька на него действуют две основные силы: сила давления рокружающей его жидкости и сила поверхностного натяжения на поверхности пузырька. Условие равновесия сил для парового пузырька сферической формы определяется уравнением Лапласа:

При избыточном давлении паровой пузырек может существовать и развиваться; при он сконденсируется. Образование пузырька с критическим радиусом R_Kвозможно лишь в том случае, если окружающая пузырек жидкость будет перегрета, т. е. если ее температура Т_Жбудет превышать температуру насыщения Т_Н(при давлении в жидкости р) на некоторую величину Dt = T_Ж — Т_Н. Температура пара Т_П,Кв пузырьке с критическим радиусом должна равняться температуре окружающих слоев жидкости Т_Ж. Поэтому температура T_Ж — Т_П,К. может быть найдена приближенно (если не учитывать малой поправки, связанной с влиянием кривизны межфазной поверхности на давление насыщения) как температура насыщения, соответствующая давлению пара внутри пузырька p1 = р+Dр. Отсюда следует, что связь между перепадом давления Dр и необходимым перегревом жидкости Dt определяется формулой

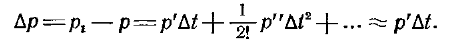
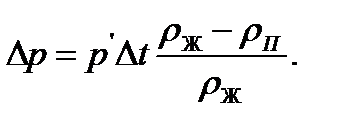
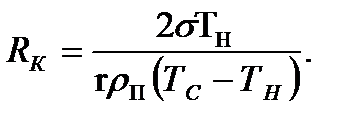
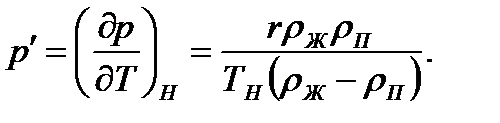
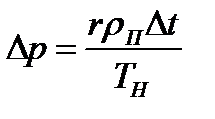
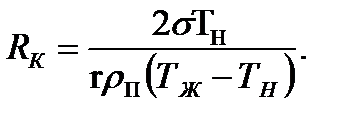Если учесть зависимость давления от кривизны поверхности раздела фаз, то

Величина р' есть производная от давления по температуре на линии насыщения, определяемая согласно закону Клапейрона — Клаузиуса уравнением

Следовательно

(13.2)

Зависимости (13.1) и (13.2) позволяют выразить критический радиус пузырька:

(13.3)

Соотношение (13-3) определяет критический радиус сферического пузырька, находящегося внутри (в объеме) перегретой жидкости вдали от поверхности нагрева.
Слои жидкости, которые непосредственно соприкасаются с поверхностью нагрева, имеют температуру T_Ж, равную температуре стенки Т_с. Поэтому если в формуле (13-3) положить T_Ж = Т_с, то

(13.4)

В такой форме записи величина R_Kхарактеризует радиус кривизны внешней поверхности пузырьков, зарождающихся на поверхности теплообмена. Одновременно величина R_Kопределяет порядок размеров тех элементов шероховатости, которые при данных условиях (давлении, перегреве и т. д.) могут служить центрами парообразования.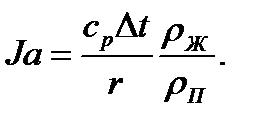
Работа, затрачиваемая на образование парового пузырька радиусом R_K, зависит от того, образуется ли паровой пузырек в объеме жидкости вдали от поверхности теплообмена или непосредственно на этой поверхности. Кроме того, работа образования пузырька будет меняться в зависимости от формы центров парообразования. В качестве центров могут быть неровности в виде впадин шероховатой поверхности, а также различные трещины, канавки и др. К наиболее благоприятным условиям образования пузырька относятся условия, при которых затрачиваемая работа будет минимальной.Работа, затрачиваемая на образование пузырька в объеме жидкости, выражается зависимостью 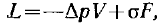где Vи F—объем и поверхность пузырьков.
Величина sFесть работа образования межфазной поверхности F. Скорость роста пузырьков зависит от интенсивности подвода теплоты обеими составляющими теплового потока. В качестве параметра, определяющего интенсивность теплообмена при кипении, может быть использовано число Якоба. Число Якоба получается при приведении системы дифференциальных уравнений и условий однозначности, описывающих теплообмен при кипении жидкости, к безразмерному виду. Для указанной системы получено уравнение подобия. Последний безразмерный комплекс, входящий в правую часть этого уравнения, является числом Якоба:

Число Якоба характеризует соотношение между тепловым потоком, идущим на перегрев еди-ницы объема жидкости, и объемной теплотой парообразования. Оно зависит от давления и перегрева жидкости. С повышением давления число Якоба уменьшается, так как существенно увеличивается плотность пара. Наоборот, с понижением давления это число увеличивается. С увеличением перегрева жидкости число Якоба растет. Размер пузыря в завершающей стадии его роста на поверхности теплообмена называется отрывным диаметром. В период возникновения и роста на пузырек действуют главным образом силы, удерживающие его в центре парообразования. С возрастанием размера пузырька увеличивается подъемная сила, стремящаяся оторвать пузырек от центра. Из равновесия сил можно получить аналитические выражения для отрывного диаметра пузырька.

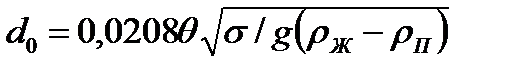величина отрывного диаметра при кипении зависит от краевого угла смачивания q. С увеличением краевого угла смачиваемость поверхности жидкости ухудшается.

30. Зависимость теплового потока от температурного напора.

При повышении температурного напора значительно возрастает поток теплоты, который отводится от поверхности нагрева к кипящей жидкости, вся эта теплота в конечном счете расходуется на образование пара. Поэтому уравнение теплового баланса при кипении имеет вид: Q = r×G, где Q — тепловой поток, Вт; r — теплота фазового перехода жидкости, Дж/кг; G — количество пара, образующегося в единицу времени в результате кипения жидкости и отводимого от ее свободной поверхности, кг/с. Тепловой поток Q при увеличении температурного напора Dt растет не беспредельно. При некотором значении Dt он достигает максимального значения, а при дальнейшем повышении Dt начинает уменьшаться. До момента достижения максимального теплового потока режим кипения называют пузырьковым.Максимальную тепловую нагрузку при пузырьковом кипении называют первой критической плотностью теплового потока н обозначают q _KР1. При больших значениях Dtнаступает второй, переходныйрежим кипения. Он характеризуется тем, что, как и на самой поверхности нагрева, так и вблизи нее пузырьки непрерывно сливаются между собой, образуются большие паровые полости. Из-за этого доступ жидкости к самой поверхности постепенно все более затрудняется. В отдельных местах поверхности возникают «сухие» пятна; их число и размеры непрерывно растут по мере увеличения температуры поверхности. Такие участки как бы выключаются из теплообмена, так как отвод теплоты непосредственно к пару происходит существенно менее интенсивно. Это и определяет резкое снижение теплового потока и коэффициента теплоотдачи в области переходного режима кипения. Наконец, при некотором температурном напоре вся поверхность нагрева обволакивается сплошной пленкой пара, оттесняющей жидкость от поверхности. Так наступает третий, пленочныйрежим кипения. Перенос теплоты в режиме пленочного кипения от поверхности нагрева к жидкости осуществляется путем конвективного теплообмена и излучения через паровую пленку. По мере увеличения температурного напора все большая часть теплоты передается за счет излучения. Интенсивность теплообмена в режиме пленочного кипения достаточно низкая. Паровая пленка испытывает пульсации: пар, периодически накапливающийся в ней, отрывается в виде больших пузырей. В момент наступления пленочного кипения тепловая нагрузка, отводимая от поверхности, и соответственно количество образующегося пара имеют минимальные значения. Минимальное значение тепловой нагрузки при пленочном кипении называет-ся второй критической плотностью теплового потока q_KP2. Таким образом, при кипении жидкости на поверхности нагрева в зависимости от температурного напора могут наблюдаться три различных режима кипения. Общая картина изменения плотности теплового потока q, отводимого к кипящей жидкости, при увеличении температурного напора Dtпоказана в логарифмических координатах на рис. Этот график относится к процессу кипения воды при атмосферном давлении. Такой же характер зависимость qот Dtимеет и для других жидкостей, кипящих в условиях свободного движения в большом объеме на металлических поверхностях нагрева: трубах, плитах и т. д.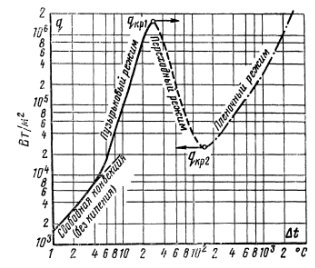

Зависимость теплоотдачи от давления и теплофизических свойств. Влияние недогрева ж