Компас не имеет дополнительного кожуха

При отклонении картушки магнитного компаса от направления меридиана магнитное поле Земли обусловит появление восстанавливающего момента М₁. Как известно [6], значение этого момента зависит от угла а, магнитного момента 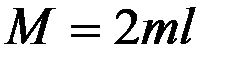картушки, напряжённости H магнитного поля Земли и абсолютной магнитной проницаемости среды :

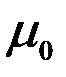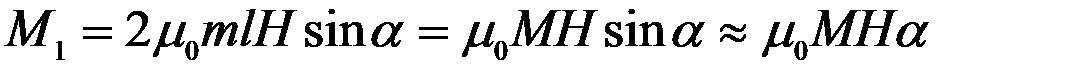. (2.1)

В выражении (2.1) принято, что углы отклонения картушки не велики и допустима замена функции 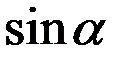её аргументом .

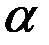Под действием момента М₁ картушка начнёт поворачиваться с некоторой угловой скоростью 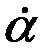и ускорением 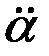. При этом возникнут моменты сил сопротивления вращению картушки, в числе которых будут:

§ момент 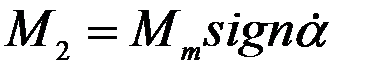сил сухого трения с амплитудным значением М_т*⁾;

§ момент 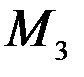= 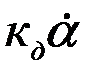сил демпфирования, возникающий за счёт трения картушки о жидкость, заполняющую котелок компаса (здесь к_д – коэффициент демпфирования);

§ момент 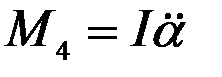сил инерции (здесь 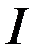- момент инерции картушки относительно оси её вращения);

§ прочие моменты М(t) внешних сил.

В соответствии с принципом Даламбера сумма всех моментов, действующих на вращающееся тело, в любой момент времени равна нулю. Использование этого принципа в рассматриваемом случае позволит записать уравнение движения картушки магнитного компаса в следующем виде:

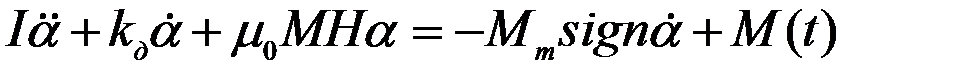. (2.2)

В нашей задаче момент М(t) будем считать равным нулю. Тогда поделив все члены уравнения (2.2) на коэффициент при первом слагаемом и приняв следующие обозначения:

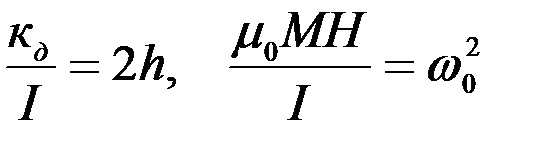, (2.3)

найдём:

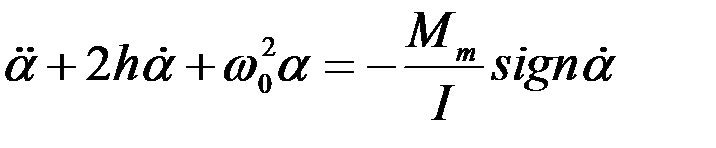. (2.4)

Мы получили неоднородное уравнение второго порядка с постоянными коэффициентами. Решение этого уравнения будем представлять в виде суммы общего решения 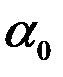однородного уравнения, полученного из (2.4) путём приравнивания нулю его правой части, и частного решения 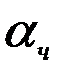неоднородного уравнения:

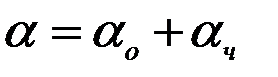. (2.5)

Однородное уравнение принимает вид:

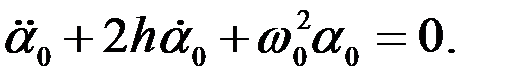(2.6)

Ему соответствует следующее характеристическое уравнение:

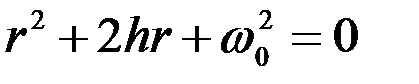, (2.7)

имеющее два корня r₁ и r₂, которые определяются известным выражением:

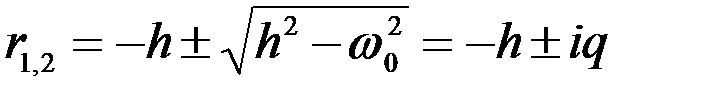, (2.8)

где .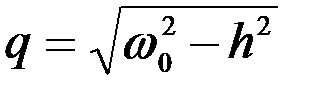

На практике параметры картушки и степень демпфирования её движения подбираются таким образом, чтобы выполнялось неравенство h < ω₀ и корни характеристического уравнения были бы комплексными. Такой выбор обеспечивает лучшие характеристики переходного процесса. В указанных условиях закон изменения угла 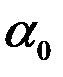примет вид:

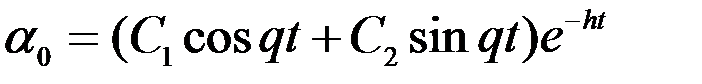, (2.9)

где С₁ и С₂ – произвольные постоянные, определяемые начальными условиями. Если считать, что в начальный момент времени картушка компаса была отклонена от меридиана на угол 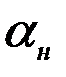, и не вращалась, то произвольные постоянные будут равны:

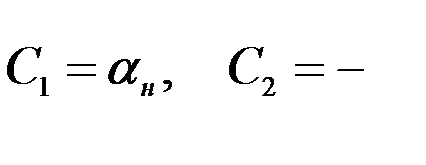
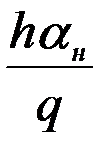, (2.10)

а искомое общее решение примет вид:

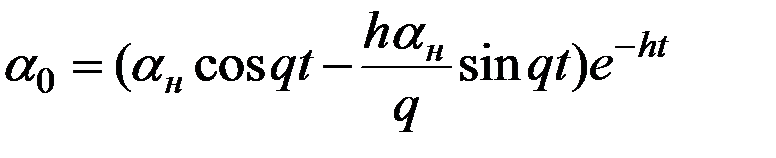. (2.11)

Полученное решение можно упростить и сделать более наглядным, если ввести следующие замены:

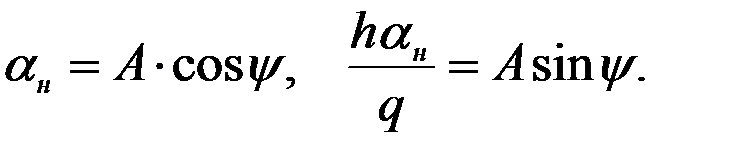(2.12)

Такое представление всегда возможно, т.к. значения А и 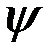определены при любых значениях и q. Действительно, если возвести оба равенства (2.12) в квадрат и затем их сложить, то найдём выражение, определяющее параметр А:

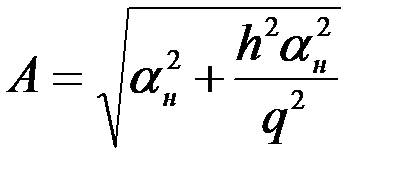. (2.13)

В свою очередь, если второе равенство (2.12) разделить на первое, получим:

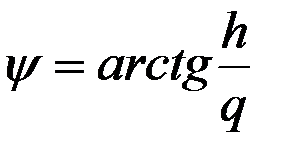. (2.14)

С учётом принятых обозначений общее решение можно представить в виде:

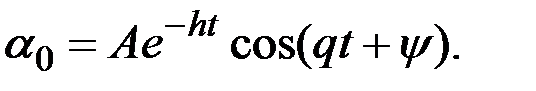(2.15)

Частное решение неоднородного уравнения (2.4) будем искать принимая во внимание, что при неизменном направлении вращения картушки компаса момент сил сухого трения остаётся постоянным и равным М_т. Это позволяет считать в установившемся режиме 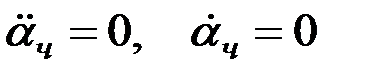. Тогда уравнение (2.4) примет вид:

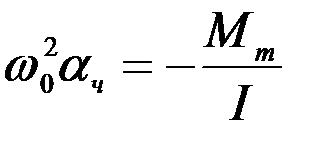, (2.16)

откуда находим:

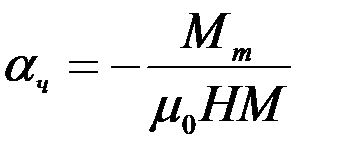. (2.17)

Общее решение исходного неоднородного уравнения с учётом полученных выражений (2.15) и (2.17) примет вид:

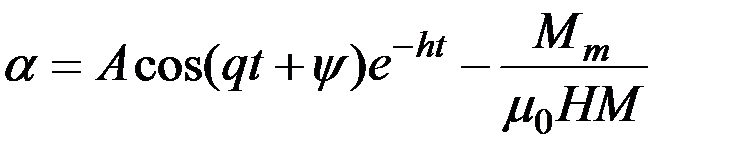. (2.18)

Зона застоя

t

α

Ае-ht

αч

А1

А2

А3

Т0

Рис. 2.11

Из полученного выражения видно, что процесс установления картушки в меридиан носит колебательный характер с амплитудой, затухающей во времени по экспоненциальному закону (рис. 2.11). С уменьшением амплитуды колебаний уменьшается значение восстанавливающего момента М₁. Когда этот момент становится равным моменту сил сухого трения движение картушки прекращается. При этом, максимальное её отклонение от меридиана будет определяться значением . 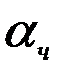Угол отклонения картушки компаса в конце переходного процесса называется углом застоя картушки, а диапазон возможных его значений – зоной застоя. Как

Важно!

следует из выражения (2.17), величина зоны застоя зависит от величины момента сил трения в опорах подвеса картушки, магнитного момента картушки и величины горизонтальной составляющей магнитного поля Земли. С целью снижения зоны застоя следует уменьшать момент сил трения (Обычно это достигают за счёт снижения радиуса трения в опоре и уменьшения остаточного веса картушки) и увеличивать собственный магнитный момент картушки.

Сам переходный процесс характеризуется его длительностью, периодом Т₀ затухающих колебаний картушки и фактором f затухания или декрементом затухания h. Длительность переходного процесса измеряется от его начала до момента остановки картушки в зоне застоя. Фактор затухания определяется отношением соседних амплитуд колебаний:

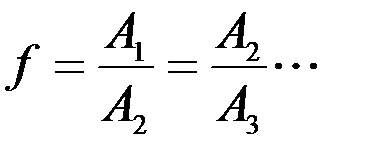. (2.19)

Если учесть, что ближайшие амплитуды связаны между собой следующим равенством:

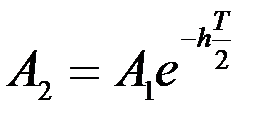, (2.20)

то нетрудно найти связь между фактором затухания и декрементом затухания:

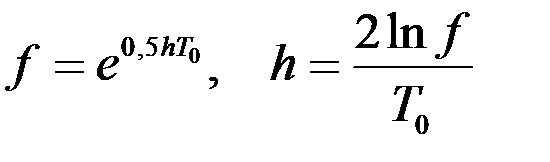. (2.21)

Все перечисленные параметры характеризуют качество работы магнитного компаса и, как правило, их количественные значения приводятся в эксплуатационной документации.