Неориентированные графы
Основные понятия теории графов
Во многих прикладных задачах изучаются системы связей между различными объектами. Впервые понятие «граф» ввёл в 1936 году венгерский математик Денни Кёниг. Но первая работа написана ещё в 1736 году Леонардом Эйлером, когда он решал знаменитую задачу о разработке замкнутого маршрута движения по мостам в городе Кенигсберге. При решении он обозначил каждую часть суши точкой, а каждый мост – линией, их соединяющей. В результате был получен граф и доказано, что задача решений не имеет. Теорию деревьев разработал немецкий физик, механик и математик Густав Кирхгоф (1824-1887). Он применил её для решения систем линейных уравнений, описывающих работу электрических цепей. Быстрое развитие теории графов получила с созданием электронно-вычислительной техники, которая позволяла решить многие задачи алгоритмизации. Теория графов в последнее время широко используется в различных отраслях науки и техники, особенно в экономике и социологии. С помощью графов изображаются схемы различных дорог, воздушных сообщений, газопроводов, теплотрасс, электросетей, а также микросхемы, дискретные многошаговые процессы, системы различных бинарных отношений, химические структурные формулы и другие диаграммы и схемы. Применяются графы для решения задач химии, экономики, электротехники и автоматики. Используются в информатике и строительстве. Без графов сложно анализировать классификации в различных науках.
Определение графа
Граф –это алгебраическая система объектов произвольной природы (вершин)и связок(рёбер), соединяющих некоторые пары этих объектов.
Несложные графы удобно изображать в виде графических схем, в которых вершины – это точки, а связи – это линии, соединяющие точки.
Обозначается G = 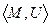 , где М – непустое конечное множество точек, а U - непустое конечное множество линий.
, где М – непустое конечное множество точек, а U - непустое конечное множество линий.
Строгое определение графа:
Графом G называется пара множеств G = 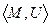 , где М – непустое конечное множество вершин { , где М – непустое конечное множество вершин { 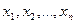 }, а элементами множества U являются некоторые двухэлементные подмножества М, т.е. U = }, а элементами множества U являются некоторые двухэлементные подмножества М, т.е. U = 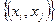 ,которые называются рёбрами. ,которые называются рёбрами.
|
При задании графа для нас не имеет значения природа связи между вершинами, важно только то, что связь существует и информация о ней содержится во множестве U.
Примеры графов: электрические цепи, географические карты, молекулы химических соединений, связи между людьми и группами людей. Граф может изображать сеть улиц в городе: вершины графа – перекрёстки, а рёбра - улицы с разрешённым направлением движения. В виде графов можно представить блок-схемы программ (вершины – блоки, а рёбра – разрешённые переходы от одного блока к другому).
По характеру связей графы разделяются на 2 класса, поэтому существует различия в терминах:
| Неориентированный (неорграф) | Ориентированный (орграф) | |
| Вид связи | Не указано направление | Указано направление |
| Точка | Вершина или узел | Вершина |
| Соединение | Ребро (отрезок) | Дуга (стрелка) |
| последовательность рёбер | Цепь | Путь |
| последовательность рёбер, у которой начальная и конечная вершины совпадают | Цикл – конечная цепь | Контур |
| Примеры графов | карта дорог | Карта туристического маршрута |
| Схема | 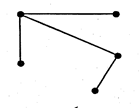
|
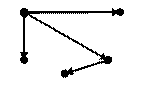
|
Неориентированные графы
Дата добавления: 2017-02-13; просмотров: 2270;











