Матрица смежности для неориентированного графа

Информация о структуре графа может быть задана матрицей бинарного отношения.

Матрица смежности для неориентированного графа – это матрица с элементами

^а_ij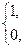_{= ,}(1,если вершина х_iсмежна с вершиной x _j_, и 0, если вершина х_iне смежнас x _j_.,)

Матрица смежности для неориентированного графа не совпадает с матрицей смежности ориентированного графа.

Если граф не имеет кратных рёбер, то матрица примет квадратный вид.

Для неориентированного графа ребро (х_i,, x _j)совпадает с ребром( x _j_, х_i),то матрица смежности будет симметрической и не меняется при транспонировании.

Хотя формально каждая вершина смежна сама себе, в матрице смежности мы будем ставить на месте 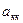= 0, если у неё нет петли, и 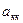= 1, если есть одна петля. Таким образом, если неограф не имеет петель, то в его матрице смежности на главной диагонали всегда стоят нули.

Изоморфизм графов.

Имея схему графа, легко записать его матрицу смежности, однако из-за неупорядоченности вершин вид матрицы зависит от выбора вершин и будет каждый раз другим. Обратная задача восстановления графа по имеющейся матрице смежности тоже приведёт к созданию графов различной формы, хоты все они будут отражать одни и те же связи между объектами. Тогда говорят, что получили граф с точностью до изоморфизма.В графах важно лишь отношение между вершинами (т.е.смежность), а их название и порядок не столь важны.

Два графа называются изоморфными (от греч. «изос» — «равный» и «морфе» — «вид», «форма»), если между их вершинами можно установить взаимно однозначное соответствие при котором вершинам, соединённым ребром, соответствуют вершины, также соединённые ребром.

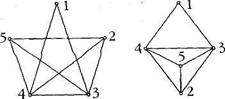
Графы изоморфны тогда и только тогда, когда их матрицы смежности получаются друг из друга одновременными перестановками строк и столбцов (т.е. одновременно с перестановкой i-ой и j-ой строк переставляются i-й и j-й столбцы).