Глава 2. Полюсные графы
Графы широко используются как структурные модели физических систем, допускающих идеализированное представление в виде схем с сосредоточенными компонентами. Соединение компонентов между собой осуществляется исключительно путем объединения их полюсов, образующих узлы схемы. В зависимости от числа полюсов различают двухполюсные и многополюсные компоненты, которые называют соответственно двухполюсниками и многополюсниками. Так, схема рис. 28 представляет собой соединение двух трехполюсников (А и В), четырехполюсника (С) и трех двухполюсников (D, Е, F).
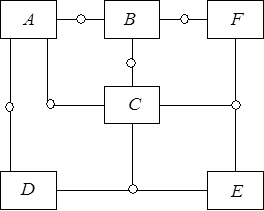
|
| Рис. 28 |
Наиболее типичными представителями физических систем, допускающих представление схемами с сосредоточенными компонентами, могут служить электрические и электронные цепи. Резисторы, конденсаторы и катушки индуктивности являются двухполюсниками а трансформаторы, электронные лампы и транзисторы – многополюсниками. Аналогичные компоненты можно выделить в системах различной физической природы: механических, акустических, гидравлических, тепловых и т. д.
Для математического описания состава и структуры физической системы (точнее, соответствующей ей схемы с сосредоточенными компонентами) обычно используются два типа соотношений:
1) полюсные уравнения, характеризующие индивидуальные свойства каждой компоненты безотносительно к возможным соединениям с другими компонентами;
2) уравнения связей, отражающие характер соединения различных компонент в схеме безотносительно к их индивидуальным свойствам.
Компонентным уравнением двухполюсника служит функциональная зависимость между двумя физическими величинами, характеризующими его состояние (например, между током и напряжением электрического двухполюсника, силой и скоростью механического двухполюсника и т. п.). Функция, описывающая нелинейный двухполюсник, может задаваться аналитическим выражением, графиком или таблицей. Линейный двухполюсник характеризуется параметром, который является либо постоянной величиной (стационарный двухполюсник), либо функцией времени (нестационарный двухполюсник).
Многополюсник описывается системой уравнений, связывающей физические величины на его полюсах. Часто многополюсные компоненты представляются схемной моделью, состоящей из двухполюсных компонентов, каждый из которых описывается соответствующей функциональной зависимостью. Но в отличие от обычных двухполюсников, такие зависимости могут содержать величины, связанные с другими компонентами схемной модели. В конечном счете, физическая система с сосредоточенными компонентами всегда может быть представлена схемой, состоящей их двухполюсников.
В роли уравнений связи обычно выступают фундаментальные физические законы, выражающие условия равновесия и непрерывности (законы Кирхгофа для электрических цепей, принцип Даламбера для механических систем и т. п.). В каждом конкретном случае эти уравнения получают из рассмотрения структуры схемы, причем они должны содержать те же величины, что и компонентные уравнения, которыми характеризуются состояния двухполюсников. Тем самым обеспечивается совместимость исходных уравнений, преобразование которых позволяет получить математическую модель системы в требуемой форме.
Схема с двухполюсными компонентами, независимо от ее конкретной физической природы, может быть представлена полюсным графом. Между схемой, состоящей из двухполюсников, и ее графом имеет место взаимнооднозначное соответствие: узлам схемы соответствуют вершины, а двухполюсникам – ребра графа. Ориентация ребра связывается с направлением отсчета физических величин, характеризующих состояние двухполюсника.
Полюсный граф является универсальной топологической моделью физических систем с сосредоточенными компонентами. Путь к такой модели лежит через идеализацию системы (схема) и ее абстрагирование (полюсный граф). Основная ценность топологических моделей состоит в том, что их свойства и методы использования можно изучать и разрабатывать независимо от физической природы систем. Специфика конкретной области проявляется на начальном этапе при построении графа и на заключительном этапе истолкования полученных результатов.
Для любого двухполюсника (рис. 29а) полюсным графом служит дуга с двумя концевыми вершинами (рис. 29б). В общем случае уравнение двухполюсника 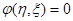 содержит две переменные содержит две переменные 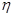 и и 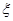 . Одна из них, например . Одна из них, например  , характеризует состояние двухполюсника относительно поперечного сечения и противоположно направлена к каждому из его полюсов. Такие переменные называют поперечными (например, электрический ток или магнитный поток, сила или момент, тепловой поток и т. п.). , характеризует состояние двухполюсника относительно поперечного сечения и противоположно направлена к каждому из его полюсов. Такие переменные называют поперечными (например, электрический ток или магнитный поток, сила или момент, тепловой поток и т. п.).
| 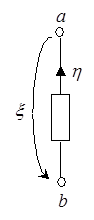
| 
|
| а | б | |
| Рис. 29 |
Другая величина  характеризует состояние двухполюсника относительно его полюсов (например, электрическое напряжение, линейная или угловая скорость, перемещение, давление, разность температур и т. п.). Такие переменные называют продольными и их направления связывают с направлением пути от одного полюса к другому. Часто поперечные переменные называют последовательными, а продольные – параллельными переменными.
характеризует состояние двухполюсника относительно его полюсов (например, электрическое напряжение, линейная или угловая скорость, перемещение, давление, разность температур и т. п.). Такие переменные называют продольными и их направления связывают с направлением пути от одного полюса к другому. Часто поперечные переменные называют последовательными, а продольные – параллельными переменными.
Если уравнение двухполюсника представимо в явном виде относительно поперечной переменной 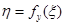 , то соответствующая ему дуга называется
, то соответствующая ему дуга называется 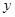 -дугой, причем величину
-дугой, причем величину  можно рассматривать как реакцию на воздействие
можно рассматривать как реакцию на воздействие  . Аналогично, если уравнение двухполюсника представимо в виде
. Аналогично, если уравнение двухполюсника представимо в виде 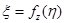 , то соответствующая ему дуга называется
, то соответствующая ему дуга называется 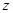 -дугой, причем величину
-дугой, причем величину 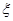 можно рассматривать как реакцию на воздействие
можно рассматривать как реакцию на воздействие 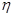 . Двухполюсники, допускающие описание относительно обеих переменных, называются взаимоопределенными, а соответствующие им дуги –
. Двухполюсники, допускающие описание относительно обеих переменных, называются взаимоопределенными, а соответствующие им дуги – 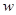 -дугами.
-дугами.
Поскольку из двух переменных 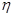 и
и 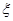 одна характеризует воздействие, а другая реакцию, то их положительные направления считают взаимно противоположными. Обычно направления дуг отождествляют с положительными направлениями отсчетов поперечных переменных, а положительные направления отсчета продольных переменных принимают обратными ориентации дуг.
одна характеризует воздействие, а другая реакцию, то их положительные направления считают взаимно противоположными. Обычно направления дуг отождествляют с положительными направлениями отсчетов поперечных переменных, а положительные направления отсчета продольных переменных принимают обратными ориентации дуг.
Полюсный граф системы строится таким образом, чтобы обеспечивались наиболее простые отношения между его структурой и уравнениями связей. Обычно уравнения связей формируются для поперечных и продольных переменных в следующем виде:
1) алгебраическая сумма поперечных переменных для любой вершины графа равна нулю: 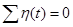 .
.
2) алгебраическая сумма продольных переменных для любого контура графа равна нулю: 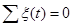 .
.
| При алгебраическом суммировании переменных они считаются положительными при совпадении их направлений с выбранным направлением относительно вершины или контура и отрицательными, если направления переменных противоположны с выбранными направлениями (рис. 30). | 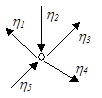
| 
|
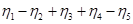
| 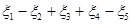
| |
| Рис. 30 |
Сначала рассматриваются методы построения полюсных графов различных физических систем с двухполюсными компонентами. В дальнейшем эти методы обобщаются на системы с многополюсниками. Для простоты компоненты предполагаются линейными и стационарными.
Существуют три типа пассивных электрических двухполюсников: сопротивление, емкость и индуктивность. Они рассеивают или накапливают энергию и поэтому называются пассивными компонентами.
| Сопротивление (рис. 31) – это такой компонент, в котором происходит необратимое преобразование электрической энергии в тепло. Зависимость между током (поперечная переменная) и напряжением (продольная переменная) может быть представлена в одной из двух форм (или в любой из них, если двухполюсник взаимоопределенный): | 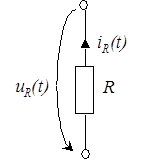
|
| Рис. 31 |
 ,
,
где параметры 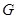 и
и 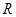 называются соответственно проводимостью и сопротивлением (
называются соответственно проводимостью и сопротивлением ( 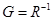 и
и 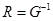 ).
).
Емкость (рис. 32) – компонент, накапливающий электрическую энергию. Заряд 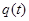 связан с напряжением связан с напряжением 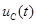 на линейной емкости соотношением на линейной емкости соотношением 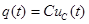 , где , где 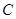 – параметр, называемый емкостью. Ток – параметр, называемый емкостью. Ток 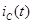 , протекающий через емкость, выражается как производная заряда по времени, следовательно: , протекающий через емкость, выражается как производная заряда по времени, следовательно:
| 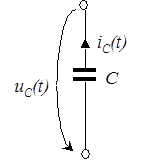
|
| Рис. 32 |
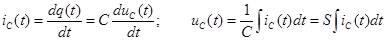 ,
,
где 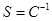 называется инверсной емкостью.
называется инверсной емкостью.
Индуктивность (рис. 33) – компонент, накапливающий магнитную энергию. Магнитный поток 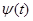 линейной индуктивности пропорционален протекающему в ней току линейной индуктивности пропорционален протекающему в ней току 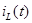 , т. е. , т. е. 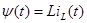 , где , где 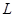 – параметр, называемый индуктивностью. Напряжение – параметр, называемый индуктивностью. Напряжение 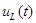 на индуктивности равно скорости изменения магнитного потока во времени, следовательно: на индуктивности равно скорости изменения магнитного потока во времени, следовательно:
| 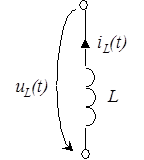
|
| Рис. 33 |
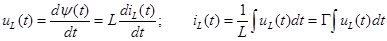 ,
,
где 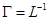 называется инверсной индуктивностью.
называется инверсной индуктивностью.
Источники энергии в электрических цепях представляются идеальными двухполюсниками двух типов.
Источник напряжения – это двухполюсник (рис. 34), напряжение в котором определяется некоторой функцией времени 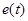 и не зависит от протекающего по нему тока, т. е. и не зависит от протекающего по нему тока, т. е. 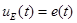 . .
| 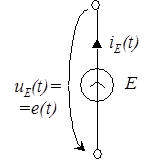
|
| Рис. 34 |
Источник тока – это двухполюсник (рис. 35), ток в котором также определяется некоторой функцией времени 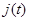 и не зависит от приложенного напряжения, т. е. и не зависит от приложенного напряжения, т. е. 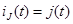 .
Для построения графа электрической схемы достаточно ее узлы рассматривать как вершины, а каждый двухполюсник заменить ребром, сохраняя отношение инцидентности. .
Для построения графа электрической схемы достаточно ее узлы рассматривать как вершины, а каждый двухполюсник заменить ребром, сохраняя отношение инцидентности.
| 
|
| Рис. 35 |
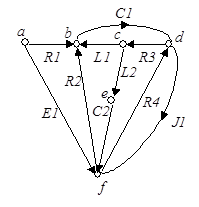
Например, граф электрической схемы (рис. 36) изображен на рис. 37.
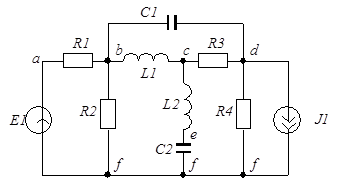
| 
|
| Рис. 36 | Рис. 37 |
Следует иметь в виду, что при изображении электрических схем линии означают проводники без сопротивления, и узлы, соединенные такими линиями, являются по существу одним узлом (узел f на рис. 36). Узлы, с которыми связаны только два двухполюсника, на схемах обычно не отмечаются (узел а рис. 36). На графах же каждая отмеченная точка рассматривается как его вершина и никаких линий, кроме дуг, не должно быть. Направления дуг пассивных двухполюсников можно выбирать произвольно. Дуги активных двухполюсников ориентируются по направлению источника тока и противоположно направлению источника напряжения (это связано с тем, что направление дуги указывает на положительное направление тока и противоположно положительному направлению напряжения).
| Удобный практический прием построения графа для данной схемы состоит в следующем. На схеме выделяется внешний контур и изображается замкнутой линией (например, окружностью), на которой размещаются соответствующие вершины. Затем граф дополняется теми ребрами и вершинами, которые отсутствуют во внешнем контуре. Так, на рис. 38 показан изоморфный граф, построенный по этому способу. | 
|
| Рис. 38 |
Уравнения связей выражаются законами Кирхгофа, представляющими условие непрерывности для токов и условие равновесия для напряжений в любой момент времени 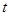 : 1) алгебраическая сумма токов для любой вершины равна нулю (первый закон Кирхгофа), т. е.
: 1) алгебраическая сумма токов для любой вершины равна нулю (первый закон Кирхгофа), т. е. 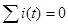 ; 2) алгебраическая сумма напряжений в любом контуре равна нулю (второй закон Кирхгофа), т. е.
; 2) алгебраическая сумма напряжений в любом контуре равна нулю (второй закон Кирхгофа), т. е. 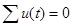 .
.
Компонент, имеющий 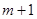 полюсов, посредством которых он может объединяться с другими компонентами, характеризуется
полюсов, посредством которых он может объединяться с другими компонентами, характеризуется 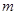 независимыми поперечными переменными
независимыми поперечными переменными 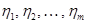 и
и 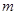 независимыми продольными переменными
независимыми продольными переменными 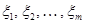 .
.
Действительно, с каждым полюсом связана поперечная переменная (рис. 39), но поскольку алгебраическая сумма поперечных переменных равна нулю, то одна из них зависима и выражается через остальные 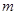 переменных. Каждая продольная переменная связана с парой полюсов и отображается соответствующим ребром. Совокупность ребер независимых переменных должна образовать дерево на множестве
переменных. Каждая продольная переменная связана с парой полюсов и отображается соответствующим ребром. Совокупность ребер независимых переменных должна образовать дерево на множестве 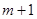 полюсов многополюсника (рис. 40). Любое другое ребро, связывающее пару каких-либо полюсов, образует с совокупностью ветвей дерева контур, и, следовательно, любая другая продольная переменная может быть выражена через некоторую совокупность
полюсов многополюсника (рис. 40). Любое другое ребро, связывающее пару каких-либо полюсов, образует с совокупностью ветвей дерева контур, и, следовательно, любая другая продольная переменная может быть выражена через некоторую совокупность 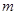 независимых продольных переменных.
независимых продольных переменных.

| 
|
| Рис. 39 | Рис. 40 |
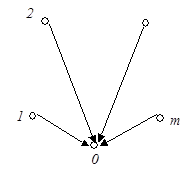
В качестве стандартного представления совокупности независимых переменных многополюсника удобно принять звездное дерево с центром в некотором полюсе, называемом базисным (рис. 41). Остальные вершины этого дерева соответствуют 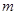 полюсам многополюсника (кроме базисного) и нумеруются порядковыми числами от 1 до
полюсам многополюсника (кроме базисного) и нумеруются порядковыми числами от 1 до 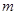 , а базисному полюсу обычно присваивается обозначение 0. Ветви дерева ориентируются одинаково относительно базисного полюса; чаще всего они направляются к базисному узлу, что соответствует направлению поперечных переменных внутрь многополюсника и продольных переменных – от базисного полюса к соответствующим полюсам (рис. 42). Таким образом, с каждым небазисным полюсом связаны продольная и поперечная переменные, которые нумеруются теми же числами, что и соответствующий полюс, и называются полюсными переменными.
, а базисному полюсу обычно присваивается обозначение 0. Ветви дерева ориентируются одинаково относительно базисного полюса; чаще всего они направляются к базисному узлу, что соответствует направлению поперечных переменных внутрь многополюсника и продольных переменных – от базисного полюса к соответствующим полюсам (рис. 42). Таким образом, с каждым небазисным полюсом связаны продольная и поперечная переменные, которые нумеруются теми же числами, что и соответствующий полюс, и называются полюсными переменными.
| 
|
| Рис. 41 | Рис. 42 |
Звездное дерево с 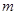 ветвями, направленными к базисному полюсу (рис. 41), представляет собой полюсный граф компоненты с
ветвями, направленными к базисному полюсу (рис. 41), представляет собой полюсный граф компоненты с 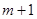 полюсами. Каждая ветвь этого графа характеризуется соответствующим уравнением системы
полюсами. Каждая ветвь этого графа характеризуется соответствующим уравнением системы 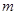 уравнений, связывающих независимые поперечные и продольные переменные многополюсной компоненты.
уравнений, связывающих независимые поперечные и продольные переменные многополюсной компоненты.
Для описания линейной компоненты с 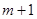 полюсами используются три различные формы соотношений, называемых полюсными уравнениями. Уравнения, записанные относительно поперечных переменных, имеют вид:
полюсами используются три различные формы соотношений, называемых полюсными уравнениями. Уравнения, записанные относительно поперечных переменных, имеют вид:
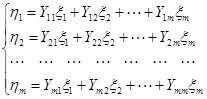
или в матричной форме 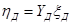 , где
, где 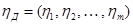 – вектор поперечных переменных;
– вектор поперечных переменных; 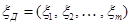 – вектор продольных переменных (оба вектора входят в уравнения как столбцевые матрицы);
– вектор продольных переменных (оба вектора входят в уравнения как столбцевые матрицы); 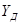 – квадратная матрица
– квадратная матрица 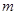 -го порядка
-го порядка
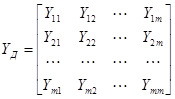 .
.
Уравнения, записанные относительно продольных переменных, имеют вид:
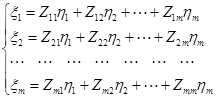
или в матричной форме 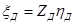 , где
, где 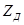 – квадратная матрица
– квадратная матрица 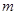 -го порядка
-го порядка
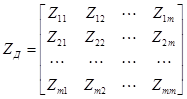 .
.
Матрицы 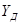 и
и 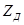 однозначно характеризуют многополюсник относительно принятой нумерации полюсов и выделенного базисного полюса и являются его обобщенными параметрами. Они связаны очевидными зависимостями
однозначно характеризуют многополюсник относительно принятой нумерации полюсов и выделенного базисного полюса и являются его обобщенными параметрами. Они связаны очевидными зависимостями
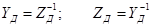 .
.
Ясно, что обе матрицы существуют в случае, когда каждая из них неособенная. Если же матрица 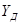 (или
(или 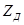 ) особенная, то матрица
) особенная, то матрица 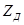 (или
(или 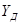 ) не существует.
) не существует.
Дуга полюсного графа многополюсника описывается тем уравнением, которое представлено относительно связанной с ней поперечной или продольной переменной (в первом случае она относится к 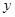 -дугам, а во втором – к
-дугам, а во втором – к 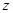 -дугам). В отличие от уравнения дуги двухполюсной компоненты, правая часть уравнения дуги полюсного графа многополюсника может содержать любые переменные, связанные с дугами этого графа.
-дугам). В отличие от уравнения дуги двухполюсной компоненты, правая часть уравнения дуги полюсного графа многополюсника может содержать любые переменные, связанные с дугами этого графа.
| В качестве примера многополюсника рассмотрим низкочастотный биполярный транзистор. Уравнения такого транзистора (рис. 43) в квазилинейном режиме обычно представляются в трех формах: | 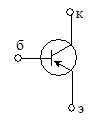
|
| Рис. 43 |
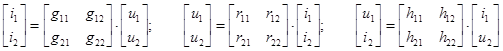 .
.
Им соответствуют три системы параметров, которыми служат матрицы 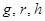 этих уравнений. Переход от одной системы параметров к другой осуществляется на основе следующих зависимостей:
этих уравнений. Переход от одной системы параметров к другой осуществляется на основе следующих зависимостей:
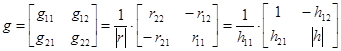 ;
;
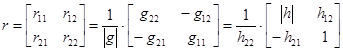 ;
;
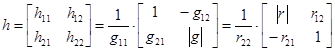 ,
,
где через 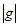 ,
, 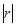 и
и 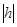 обозначены определители соответствующих матриц, т. е.
обозначены определители соответствующих матриц, т. е. 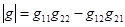 и т. п.
и т. п.
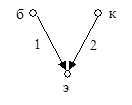
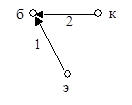
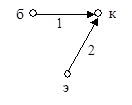
В зависимости от того, какой из трех полюсов транзистора выбран базисным (общим), имеем три типа полюсных графов: с общим эмиттером (рис. 44), с общей базой (рис. 45) и с общим коллектором (рис. 46).
| 
| 
|
| Рис. 44 | Рис. 45 | Рис. 46 |
Для описания дуг каждого из этих полюсных графов пригодна любая из трех форм уравнений. Разумеется, численные значения параметров для различных полюсных графов отличаются между собой, поэтому параметры отличают индексами (э, б, к) соответственно схеме, в которой они определены.
Вид графа транзисторной схемы зависит от выбора базисных полюсов транзисторов. Так, для схемы (рис. 47) при общей базе для первого транзистора и общем эмиттере для второго транзистора получаем граф, изображенный на рис. 48 (дуги полюсных графов транзисторов выделены жирными линиями).
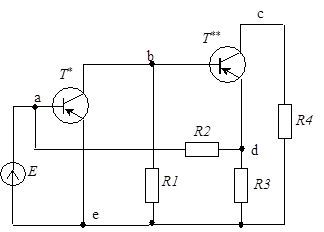
| 
|
| Рис. 47 | Рис. 48 |
Один из распространенных методов представления многополюсных компонентов основан на использовании их схемных моделей, состоящих из двухполюсников и называемых часто схемами замещения или эквивалентными схемами. Вид схемной модели компонента зависит от режима его работы, требуемой точности описания его свойств и поставленной задачи. В качестве примера рассмотрим две схемные модели транзистора. Одна из них (рис. 49) является высокочастотной моделью в квазилинейном режиме (при слабых сигналах).
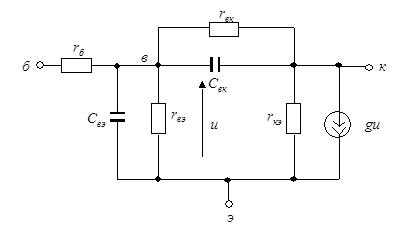
|
| Рис. 49 |
Она содержит линейные резистивные и емкостные двухполюсники и источник, ток которого 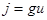 линейно зависит от напряжения
линейно зависит от напряжения 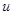 между узлами в и э.
между узлами в и э.
Вторая, называемая моделью Эберса – Молла (рис. 50), представляет транзистор в режиме больших сигналов и содержит нелинейные емкости (Cкб, Сэб, Скд, Сэд) и нелинейные резисторы (Дк, Дэ), а также источники, токи которых выражаются через токи 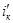 и
и 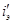 посредством коэффициентов
посредством коэффициентов 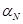 и
и 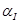 .
.

|
| Рис. 50 |
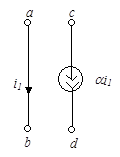
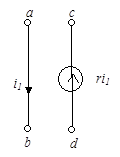
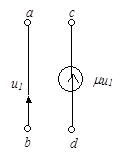
Характерной особенностью схемных моделей многополюсных компонентов является наличие в них зависимых источников, токи или напряжения которых могут зависеть от токов или напряжений в любой части схемы. На рис. 51 показаны четыре основные типа зависимых источников: источники тока, управляемые током (рис. 51а) или напряжением (рис. 51б), и источники напряжения, управляемые током (рис. 51в) или напряжением (рис. 51г).
| 
| 
| 
| 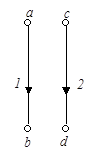
|
| а | б | в | г | д |
| Рис. 51 |
Величины 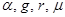 , являющиеся коэффициентами пропорциональности в уравнениях зависимых источников, называют управляющими параметрами.
, являющиеся коэффициентами пропорциональности в уравнениях зависимых источников, называют управляющими параметрами.
Полюсный граф зависимого источника, в отличие от обычного двухполюсника, состоит из двух дуг (рис. 51д). Первая из них отображает величину (ток или напряжение), которая управляет зависимым источником и называется управляющей дугой. Вторая представляет собственно источник и называется управляемой дугой.
Чаще всего управляющие величины связаны с некоторыми двухполюсниками схемы (например, величину 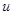 на рис. 49 можно рассматривать как напряжение на двухполюсниках
на рис. 49 можно рассматривать как напряжение на двухполюсниках 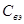 или
или 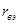 , а управляющие токи
, а управляющие токи 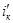 и
и 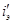 на рис. 50 – как токи двухполюсников Дк и Дэ. В таких случаях роль управляющей дуги играет дуга того двухполюсника, ток или напряжение которого управляет зависимым источником. В общем случае управляющие величины фиксируются в полюсном графе короткозамкнутыми (для тока) и разомкнутыми (для напряжения) дугами. Аналогичные дуги можно вводить в полюсный граф для фиксации любых токов и напряжений, непосредственно не связанных с компонентами, но представляющих интерес при анализе системы (например, входные и выходные величины, напряжение между любой парой узлов, ток в любом проводнике и вообще любая искомая величина).
на рис. 50 – как токи двухполюсников Дк и Дэ. В таких случаях роль управляющей дуги играет дуга того двухполюсника, ток или напряжение которого управляет зависимым источником. В общем случае управляющие величины фиксируются в полюсном графе короткозамкнутыми (для тока) и разомкнутыми (для напряжения) дугами. Аналогичные дуги можно вводить в полюсный граф для фиксации любых токов и напряжений, непосредственно не связанных с компонентами, но представляющих интерес при анализе системы (например, входные и выходные величины, напряжение между любой парой узлов, ток в любом проводнике и вообще любая искомая величина).
Короткозамкнутая управляющая (или фиксирующая) дуга описывается уравнением 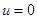 и поэтому всегда является
и поэтому всегда является 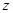 -дугой. Разомкнутая управляющая (или фиксирующая) дуга описывается уравнением
-дугой. Разомкнутая управляющая (или фиксирующая) дуга описывается уравнением 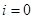 и относится к
и относится к 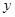 -дугам. Управляемые дуги зависимых источников тока в соответствии с их уравнениями
-дугам. Управляемые дуги зависимых источников тока в соответствии с их уравнениями 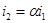 или
или 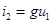 являются
являются 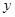 -дугами, а управляемые дуги зависимых источников напряжения в соответствии с уравнениями
-дугами, а управляемые дуги зависимых источников напряжения в соответствии с уравнениями 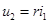 или
или 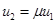 являются
являются 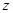 -дугами.
-дугами.
Представление многополюсных компонентов схемными моделями применимо не только к электронным, но и к другим системам, а изложенные здесь положения распространяются на них по аналогии.
Дата добавления: 2016-09-06; просмотров: 2612;











