Алгоритм Краскала построения минимального остовного дерева

Пусть G(V,E) – связный нагруженный граф с p вершинами.

1. В качестве первого ребра искомого минимального каркаса выбираем ребро e1 с наименьшим весом μ(e1). Если таких рёбер несколько, то берем любое из них.

2. На каждом из следующих шагов добавляем самое короткое из оставшихся рёбер ei, при присоединении которого к уже выбранным рёбрам не образуется никакого цикла. Если имеется несколько рёбер одинаковой длины, то выбираем любое из них.

3. Указанный процесс продолжается до тех пор, пока к выбранному множеству рёбер нельзя добавить ребро без появления цикла. Полученный подграф и является минимальным каркасом исходного графа, и называется экономическим деревом.

Практика

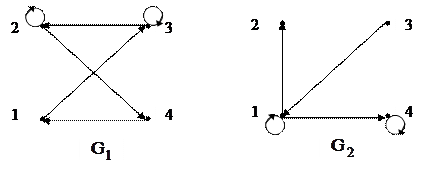
Задача № 1. Для графов G₁ и G₂ построить графы G₁ÈG₂, G₁ÇG₂, G₁(G₂), G₂(G₁), матрицы смежности вершин А(G₁), А(G₂) и матрицы инцидентности В(G₁), В(G₂), введя предварительно нумерацию дуг. По матрицам смежности вершин исходных графов построить матрицы смежности вершин А(G₁ÈG₂), А(G₁ÇG₂), А(G₁(G₂)), А(G₂(G₁)). Будут ли изоморфны графы G₁(G₂) и G₂(G₁)?

Задача № 2. По алгоритму Краскала построить для нагруженного графа G, минимальный каркас G₁ с указанием последовательности выбора рёбер e_i. Определить вес построенного каркаса m(G₁).

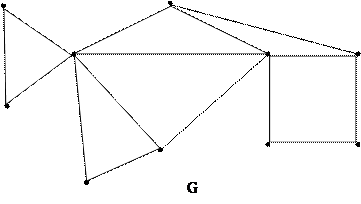v₂ v₄

3 1 2 3

1 2 v₃ 3 v₅ 4 v₈

v₁ 3 5 2 1

4 v₆ v₁₀ v₉

v₇

Задача о дороге

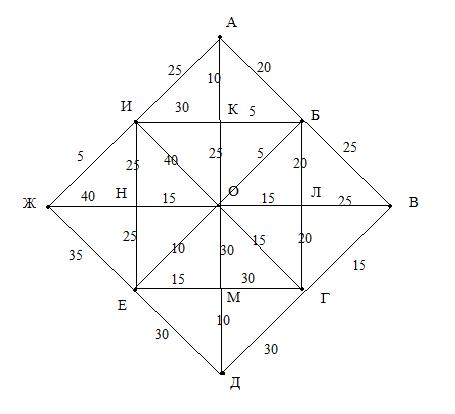
Успеет ли моя мама добраться из дома, который находится в пункте А, до вокзала, который находится в пункте Д, если поезд отправляется через час? На рисунке показано, какое время в минутах потрачено на дорогу из одного пункта в другой.

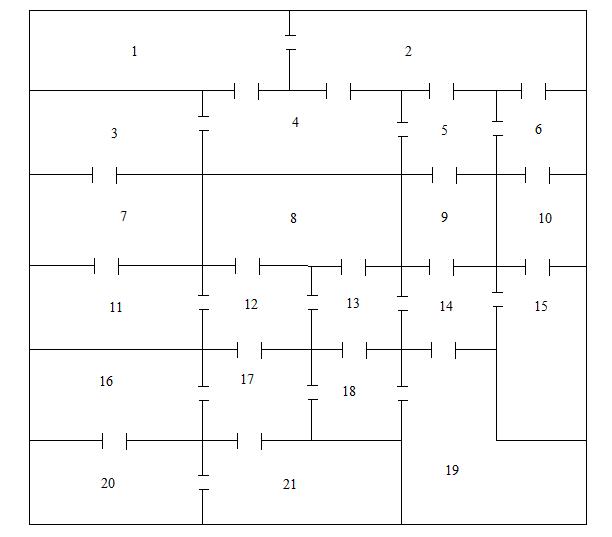
Лабиринт

На рисунке изображен план подземелья, в одной из комнат которого скрыты богатства рыцаря. После его смерти наследники нашли завещание, в котором было сказано, что для отыскания сокровищ достаточно войти в одну из крайних комнат подземелья, пройти через все двери, причем точно по одному разу через каждую. Сокровища скрыты за дверью, которая будет пройдена последней. В какой комнате скрыты сокровища?