Представление о законе больших чисел

Рассмотрим последовательность с.в. {X_n} c м.о. 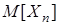. Обозначим 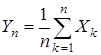– среднее арифметическое с.в., 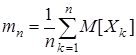– среднее арифметическое м.о. Закон больших чисел – это теорема, которая при выполнении некоторых условий утверждает о том, что

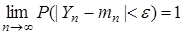"e > 0. (6.2)

Смысл этого равенства заключается в том, что при достаточно большом n значения с.в. Y_n близки числу m_n .

Теорема Чебышева (закон больших чисел). Если с.в. последовательности {X_n} независимы и их дисперсии ограничены одним числом, то верно равенство (6.2).

Следствие (закон больших чисел). Если случайные величины последовательности {X_n} независимы имеют одинаковые м.о. а и одинаковые дисперсии, то имеет место равенство

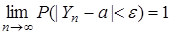"e > 0. (6.3)

Так как 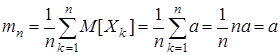, то равенство (6.3) частный случай равенства (6.2).

В практике измерения некоторой неизвестной величины часто пользуются следующим способом. Эта величина измеряется несколько раз (n раз), а затем за истинное значение измеряемой величины берется среднее арифметическое измеренных значений. Правомерность такого способа основывается на законе больших чисел.

Рассмотрим опыт в схеме Бернулли (см. п.2.6 и п. 5.1) с вероятностью успеха p, вероятностью неудачи q =1– p. Успеху сопоставим 1, а неудаче – 0. Тогда результатом опыта является случайная величина Х c законом распределения 0®q, 1®p. 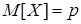, 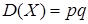(см. п.5.1). Обозначим k случайную величину, равную числу успехов в n независимых повторениях опыта. Величина 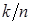называется относительной частотой успеха.

Теорема Бернулли (закон больших чисел). В схеме Бернулли для относительной частоты выполняется равенство

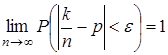"e > 0. (6.4)

Равенство (6.4) является частным случаем равенства (6.2). Действительно, случайную величину k можно рассматривать как сумму с.в. 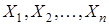, распределенных так же как и Х. Тогда средняя арифметическая этих с.в. 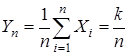, а м.о. каждой слагаемой с.в. равно p.

Смысл теоремы состоит в том, что при больших n относительная частота события примерно равна вероятности появления этого события в одном опыте. В частности, теорема Бернулли подтверждает тот факт, что при многократном подбрасывании монеты герб появляется примерно в половине случаев.