Представление о центральной предельной теореме

Рассмотрим последовательность с.в. 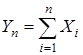(n = 1,2,…). Под центральной предельной теоремой понимается теорема, устанавливающая условия, при которых сумма случайных величин Y_n при n®¥ стремится к случайной величине, распределенной по нормальному закону.

Ниже приведем нестрогую формулировку центральной предельной теоремы Ляпунова.

Теорема Ляпунова. Пусть последовательность с.в. {X_n} (n=1,2,…) удовлетворяет следующим условиям:

1) " n 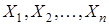независимы;

2) " i X_i имеет конечные математическое ожидание и дисперсию;

3) выполняется условие Ляпунова.

Тогда функция распределения с.в. 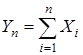при n®¥ стремится к функции нормального распределения с м.о. 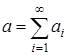и дисперсией .

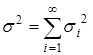Точное условие Ляпунова приводить не будем (его можно посмотреть в [Кремер]). Его содержательный смысл состоит в том, что вклад каждого слагаемого X_i в сумму Y_n при больших n ничтожно мал. Эта теорема объясняет тот факт, что в природе часто встречаются нормально распределенные с.в. Так, естественные размеры (рост человека, высота дерева) имеют нормальное распределение. Например, на высоту дерева влияют множество независимых факторов, каждый из которых существенно не влияет на общее действие всех факторов.