Анализ чувствительности.

Одной из задач анализа проекта является определение чувствительности показателей эффективности к изменениям различных параметров. Необходимо анализировать устойчивость проекта к возможным изменениям как экономической ситуации в целом (изменение структуры и темпов инфляции, увеличении сроков задержки платежей), так и внутренних показателей проекта (изменение объемов сбыта, цены продукции). Такой анализ называется анализом чувствительности.

Анализ чувствительности позволяет ответить на вопрос: «Что будет, если значение такого-то фактора изменится на столько-то?»

Анализ чувствительности дает возможность провести сравнительный анализ вариантов проекта.

Этапы анализа чувствительности:

- выделение ключевых параметров проекта (NPV, IRR, FV и т. д.), изменение которых существенно отразится на потоках проекта и влияющих на их значения факторах (выручка, себестоимость, зарплата, налоги и т. д.);

- расчет ключевых параметров при базовых значениях факторов;

- последовательное изменение факторов и расчет ключевых параметров при новых условиях;

- проверка чувствительности выбранных параметров при вероятности отклонений первого типа (вероятность того, что фактор изменится, то есть станет больше, меньше или останется плановым) и второго типа (если фактор все же окажется ниже планового уровня, то с вероятностью 60% отклонение будет не более 10%);

- определение наиболее чутких к этим изменениям ключевых параметров и факторов, оказывающих самое большое воздействие;

- сравнение чувствительности проекта по каждому фактору.

Исследование чувствительности показателей эффективности к изменению ставки дисконтирования позволяет определить устойчивость проекта по отношению к колебаниям конъюнктуры финансового рынка и возможным изменениям макроэкономических условий деятельности (рис. 5.3).

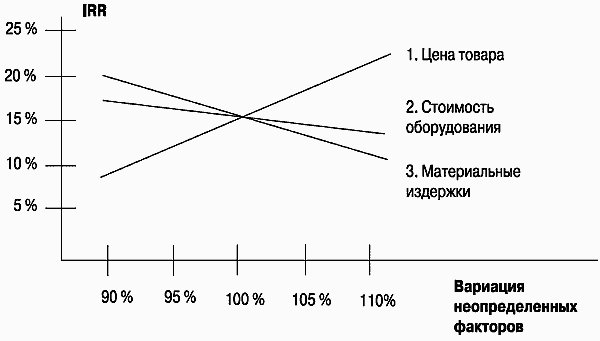
Рис. 5.3. Анализ чувствительности в графиках (пример)

Чем шире диапазон параметров, в котором показатели эффективности остаются в пределах приемлемых значений, тем выше запас прочности проекта, тем лучше он защищен от колебаний различных факторов, оказывающих влияние на результаты реализации проекта.

Факторный анализ.

Факторный анализ – группа методов многомерного статистического анализа, которые позволяют представить в компактной форме обобщенную информацию о структуре связей между наблюдаемыми признаками изучаемого объекта на основе выделения некоторых непосредственно не наблюдаемых факторов (рис. 5.4). Факторный анализ определяет предполагаемые факторы риска и степень их воздействия на деятельность компании или на проект.

Выделяют четыре основных метода факторного анализа:

1) метод цепных подстановок – используется для расчета влияния факторов во всех типах детерминированных факторных моделей: аддитивных, мультипликативных, кратных и смешанных (комбинированных). Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде. С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, трех и последующих факторов, допуская, что остальные не меняются. Сравнение величины результативного показателя до и после изменения уровня того или другого фактора позволяет элиминировать влияние всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя;

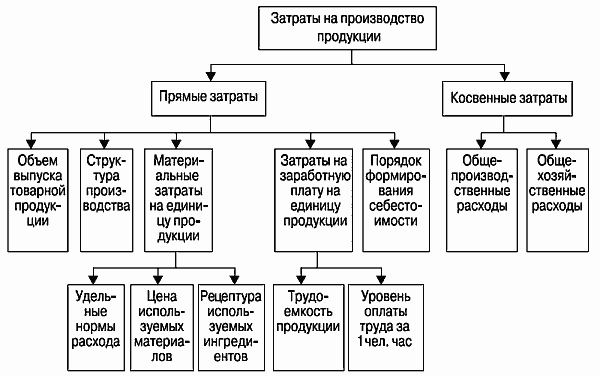
Рис. 5.4. Пример факторного анализа (система факторов величины

затрат на производство)

2) интегральный метод – позволяет достигнуть полного разложения результативного показателя по факторам и носит универсальный характер – применяется для измерения влияния факторов в мультипликативных (f = x*y; f = x*y*z), кратных (f = x/y) и смешанных (f = x/(y+z)) моделях.

Позволяет получить более точные результаты вычисления влияния факторов по сравнению со способами цепной подстановки, абсолютных и относительных разниц и избежать неоднозначной оценки влияния: в данном случае результаты не зависят от местоположения факторов в модели, а дополнительный прирост результативного показателя, возникающий из-за взаимодействия факторов, распределяется между ними поровну;

3) индексный метод – основан на относительных показателях динамики, пространственных сравнений, выполнения плана, выражающих отношение фактического уровня анализируемого показателя в отчетном периоде к его уровню в базисном периоде (или к плановому или по другому объекту).

С помощью агрегатных индексов можно выявить влияние различных факторов на изменение уровня результативных показателей в мультипликативных и кратных моделях;

4) дифференцирование – предполагается, что общее приращение функций (результирующего показателя) разлагается на слагаемые, где значение каждого из них определяется как произведение соответствующей гибкой производной на приращение переменной (фактора), по которой исчислена данная производная. В этом методе так называемый неразложимый остаток, который интерпретируется как логическая ошибка метода дифференцирования, просто отбрасывается. В этом состоит «неудобство» дифференцирования для экономических (особенно бухгалтерских) расчетов, в которых. как правило, требуется точный баланс изменения результативного показателя и алгебраической суммы влияния всех факторов..

Метод Монте-Карло.

Цель метода Монте-Карло (статистического анализа) состоит в определении степени воздействия случайных факторов на показатели эффективности проекта. Метод основан на сборе и обработке больших массивов данных как о проекте (компании), так и о внешней среде, с использованием статистических методов и моделей. На практике метод применяется редко.

Анализ производится следующим образом. Допустим, мы определили, какие именно данные следует признать неопределенными, а также установили диапазон значений, в пределах которого они могут изменяться случайным образом. Если речь идет, например, о двух параметрах, это означает, что определена область значений исходных данных, имеющая форму прямоугольника.

Для трех переменных эта область представляет собой параллелепипед, а для L-переменных – L-мерный параллелепипед. В любом случае совокупность исходных данных, от которых зависит судьба проекта, отображается точкой, лежащей внутри выделенной области. Таких точек великое множество, поэтому выполнить расчет проекта для каждой из них невозможно. Тем не менее необходимо определить, какое воздействие оказывает неопределенность исходных данных на поведение модели.

Предположим, в нашем распоряжении имеется способ выбирать точки в выделенной области данных случайным образом, аналогично рулетке в игорном заведении. Для каждой выбранной таким способом точки мы проведем расчет показателей эффективности и запишем их в таблицу. Проделав достаточно большое количество опытов, мы можем подвести некоторые итоги.

Для количественной оценки результатов используются два критерия: среднее значение и неопределенность.

Предположим, мы проделали N опытов и получили набор значений некоторого показателя fn (n = 1,…, N). Тогда среднее значение M определяется по формуле:

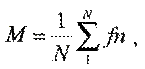
Неопределенность (или коэффициент вариации) рассчитывается следующим образом:

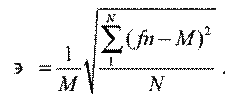
Величину М можно интерпретировать как ожидаемое значение случайной величины fn, а Э – как характеристику рассеяния значений fn. Чем меньше Э, тем ближе лежат значения fn друг к другу, тем точнее средняя величина М характеризует ожидаемое значение fn.

Неопределенность можно рассматривать так же, как оценку риска, связанного с тем, что значение fn отклонится от ожидаемой величины М.

Экспертный анализ.

Экспертный анализ устанавливает степень воздействия риска на компанию (проект) путем экспертных оценок специалистов в этой области.

При анализе рисков формируется таблица экспертного мнения (табл. 5.1).

Таблица 5.1