Расчет по допускаемым напряжениям

Расчет состоит из 3-х этапов.

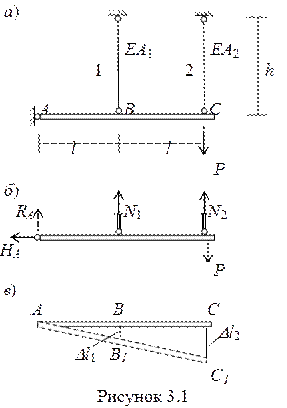
1 Статическая сторона задачи (рисунок 3.1,б) – записываем возможные уравнения статики, рассматривая равновесие стержня АС.

Sm_A = 0. N₁ ·l + N₂ ·2l - P·2l = 0.

N₁ + 2N₂ = 2P. (а)

Из уравнения (а) следует, что задача один раз статически неопределима.

2 Геометрическая сторона задачи, предполагающая вывод уравнения совместности деформаций. Для записи этого уравнения покажем деформированное состояние стержневой системы (рисунок 3.1,в). В результате приложения силы Р жесткий брус АС повернется вокруг точки А в положение АС₁, оставаясь прямым в силу большой жесткости. Стержни 1 и 2 получат деформации растяжения Dl₁ и Dl₂. Из подобия треугольников АВВ₁ и АСС₁ запишем:

,

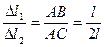откуда: Dl₂ = 2Dl₁. (б)

Уравнение (б) является уравнением совместности деформаций для рассматриваемой задачи.

3. Физическая сторона задачи. Поскольку уравнения (а) и (б) содержат разные переменные N и Δl, выразим перемещения через усилия:

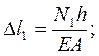
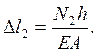(в)

Подставляя (в) в (б) получим второе уравнение, содержащее в качестве неизвестных усилия N_i.

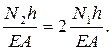
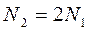. (г)

Решаем совместно уравнения (а) и (г).

N₁ = 0,4P, N₂ = 0,8P. .

Наибольшее усилие и, соответственно, наибольшее напряжение возникает во 2 стержне, для которого и записано условие прочности. Тогда безопасная нагрузка составит

[P] = 1,25s_тА/n. (3.3)

Проведенный выше расчет называется расчет по допускаемым напряжениям. Напряжения в подвесках в данном случае составляют:

s₂ = [s] = 160 МПа,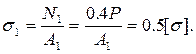

то есть только в одном (втором) стержне напряжения достигают [s], в первом стержне напряжения меньше допускаемых.

3.2.2 Расчет по предельному состоянию.

Расчет по предельному состоянию основан на предположении, что предельное состояние системы наступит тогда, когда в обоих стержнях системы напряжение будет равно пределу текучести. Такое предположение возможно, если воспользоваться упрощенной диаграммой s(e) - диаграммой Прандтля (рисунок 4), в которой отсутствует участок упрочнения, которое в реальных материалах наступает после достижения предела текучести (показано пунктиром).

s₁ = s₂ = s_т.

 

Усилия в стержнях составят:

 

N₁ = s_т·A₁, N₂ = s_т·A₂.

 

Подставим эти значения усилий в уравнение равновесия (а) и определим предельную нагрузку Р_пред, при которой оба стержня «потекут»:

s_т·A₁ + 2s_т·A₂ =2Р_пред.

Р_пред = 1,52s_т·A .

Определим безопасную нагрузку [P]_пр при расчете по предельному состоянию:

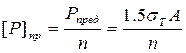, (3.4)

которая больше допускаемой нагрузки [P], полученной при расчете по допускаемым напряжениям, на 20%.

Таким образом, расчет по предельному состоянию позволяет более оптимально использовать несущую способность статически неопределимой системы.