Примеры расчета статически неопределимой рамы методом
Перемещений
Пример 2.1. Построить эпюры внутренних усилий для рамы, показанной на рисунке 2,10, а.
Решение.
1 Проводим кинематический анализ стержневой системы. Степень статической неопределимости W = 3∙1 - 2∙0 – 7 = - 4, степень кинематической неопределимости n = nу + nл = 1 + 0 = 1.
2 Выбираем основную систему метода перемещений (рис. 2.10, б).
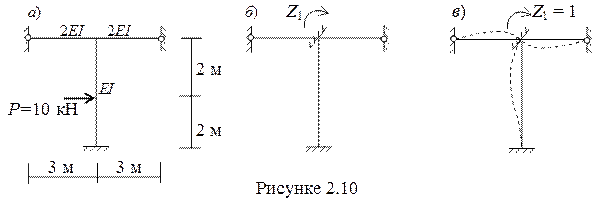
3 Записываем каноническое уравнение метода перемещений
Z1r11 + R1p = 0.
4 Для определения единичной r11 и грузовой R1P реакций строим единичную (рисунок 2.11,а) и грузовую (рисунок 2.11,в) эпюры, пользуясь Таблицей реакции (Приложение В). На рисунках 2.10,в и 2.11,б показаны единичное и грузовое состояния.
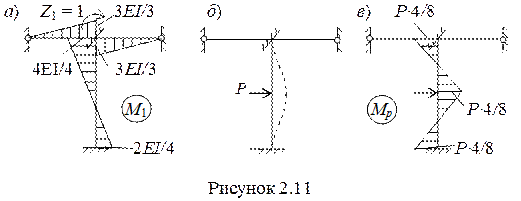
5 Рассматривая равновесие узлов (рисунок 2.12), имея ввиду уравнение
∑m = 0, определяем значения реакций.
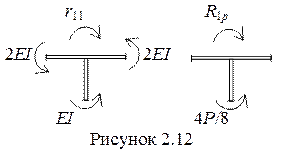
|
r11 = 2EI + 2EI + EI = 5EI,
R1p = 4P/8 = 5 кН.
6 Решаем каноническое уравнение и определяем значение неизвестного. Напомним, что это угол поворота жесткого узла.
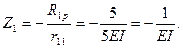
7 Строим эпюру М1, как: М1 = 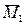 ×Х1 (рисунок 2.13, а)и, далее, строим результирующую эпюру М, в виде суммы М = М1 + МР (рисунок 2.13, б). Проводим проверку равновесия жесткого узла.
×Х1 (рисунок 2.13, а)и, далее, строим результирующую эпюру М, в виде суммы М = М1 + МР (рисунок 2.13, б). Проводим проверку равновесия жесткого узла.

|
Статическая проверка узла

|
8 Путем графического дифференцирования строим эпюру Q и, рассматривая равновесие узла, определяем и строим эпюру N (рисунок 2.15).

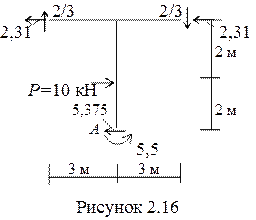
9 Выполняем статическую проверку рамы в целом (рисунок 2.16).
|
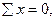
- 2,31 + 10 -2,31 – 5,375 = 10 – 9,995 ≈ 0,
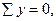
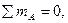
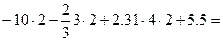
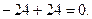
Уравнения равновесия выполняются.
Пример 2.2Построить эпюры внутренних усилий для рамы, показанной на рисунок 2.17,а.
Решение.
Порядок расчета аналогичен предыдущему примеру 2.1.
1 Проводим кинематический анализ стержневой системы. Степень статической неопределимости W = 3∙1 - 2∙0 – 7 = - 4, степень кинематической неопределимости n = nу + nл = 0 + 1 = 1.
2 Выбираем основную систему метода перемещений (рис. 2.17, б).
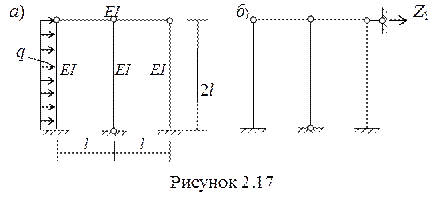
3 Записываем каноническое уравнение метода перемещений
Z1r11 + R1p = 0.
4 Для определения единичной r11 и грузовой R1P реакций строим единичную (рисунок 2.18,б) и грузовую (рисунок 2.19,б) эпюры, используя таблицы реакций.
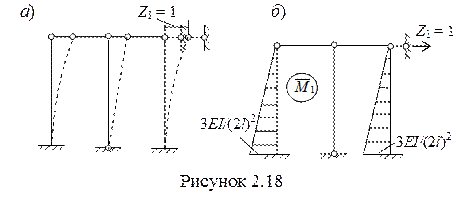
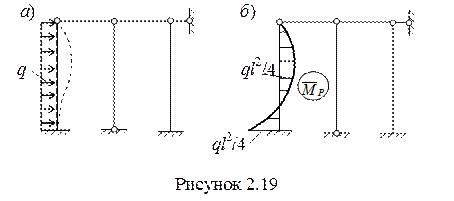
5 Рассматривая равновесие ригеля рамы (рисунок 2.20), имея ввиду уравнение ∑х = 0, определяем значения реакций в наложенной связи.
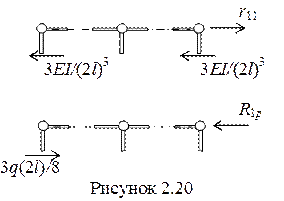
|
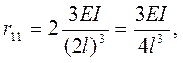
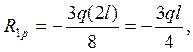
6 Решаем каноническое уравнение и определяем значение неизвестного. В этой задаче неизвестным является горизонтальное смещение ригеля..
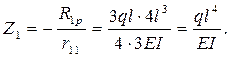
7 Строим эпюру М1, как: М1 = 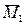 ×Х1 (рисунок 2.21, а)и, далее, строим результирующую эпюру М, в виде суммы М = М1 + МР (рисунок 2.21, б).
×Х1 (рисунок 2.21, а)и, далее, строим результирующую эпюру М, в виде суммы М = М1 + МР (рисунок 2.21, б).

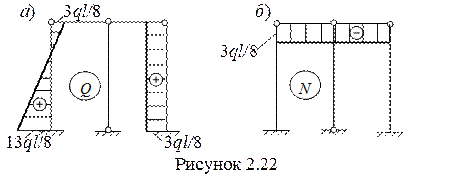
8 Путем графического дифференцирования строим эпюру Q и, рассматривая равновесие узлов, определяем продольные усилия и строим эпюру N (рисунок 2.22).
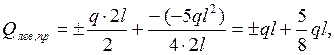
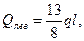
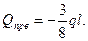
9 Выполняем статическую проверку рамы в целом (рисунок 2.23).
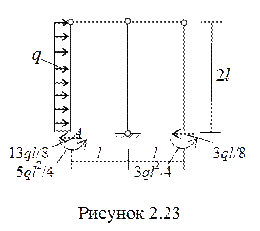
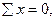 q×2l – 13ql/8 – -3ql/8 = 0,
q×2l – 13ql/8 – -3ql/8 = 0,
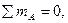
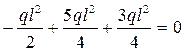
Уравнения равновесия выполняются.
|
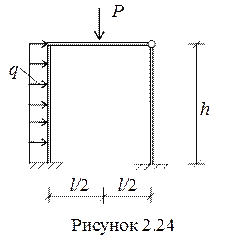
Пример 2.3 Для заданной статически неопределимой рамы, показанной на рисунке 2.24, требуется построить эпюры внутренних усилий. Исходные данные: l = 4 м, h = 6 м, q = 2кН/м, Р = 10 кН, EI = const.
Решение.
1 Степень кинематической неопределимости рассматриваемой рамы составляет
n = nу + nл = 1 + 1 = 2.
2 Система канонических уравнений в данном случае имеет вид
z1∙r11 + z2∙r12+ R1Р = 0,
z1∙r21 + z2∙r22+ R2Р = 0.
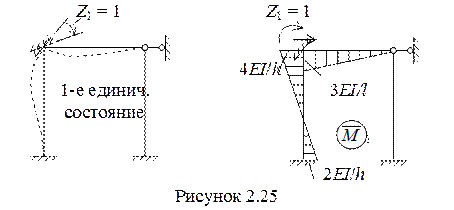
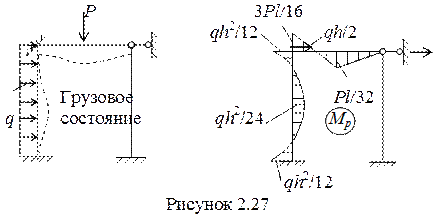
3 Используя таблицы (см. приложение В) строим единичные и грузовую эпюры. Для этого последовательно создаем единичные и грузовое состояния с показом ожидаемого деформированного вида, которые показаны на рисунках 2.25, 2.26, 2.27. Это помогает правильно воспользоваться таблицами реакций для построения эпюр изгибающих моментов. Необходимо помнить, что эпюры М строятся на растянутых волокнах.
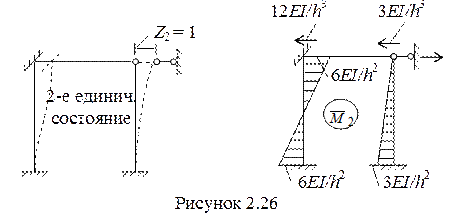
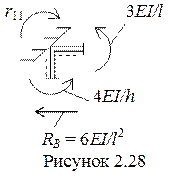
|
4 Вычисляем единичные коэффициенты.
Для вычисления реакции r11 вырежем узел с заделкой на эпюре 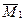 (рисунок 2.25) и рассмотрим его равновесие под действием реактивных моментов, возникающих по концам стержней и реакции в заделке r11, которую направляем по направлению единичного воздействия Z1 = 1.
(рисунок 2.25) и рассмотрим его равновесие под действием реактивных моментов, возникающих по концам стержней и реакции в заделке r11, которую направляем по направлению единичного воздействия Z1 = 1.
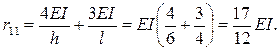
Во втором единичном состоянии при отклонении вправо в стержнях появляются реакции, направленные влево (рисунок 2.26). Тогда
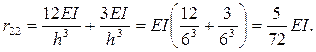

|
При определении побочных коэффициентов (т. е. реакций) воспользуемся правилом, что r12 = r21. Рассмотрим эпюру 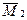 , где наглядно видно, что в первой наложенной связи при смещении Z2 = 1 возникает момент 6EI/h2, растягивающий правые волокна (рисунок 2.26) – направленный в сторону перемещения Z1.
, где наглядно видно, что в первой наложенной связи при смещении Z2 = 1 возникает момент 6EI/h2, растягивающий правые волокна (рисунок 2.26) – направленный в сторону перемещения Z1.
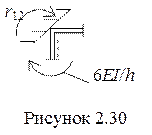
|
Реакция r12 будет равна:
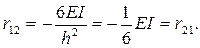
При определении знака поперечной реакции удобно пользоваться правилом знаков для поперечной силы – положительная поперечная сила вращает узел по часовой стрелке.
|
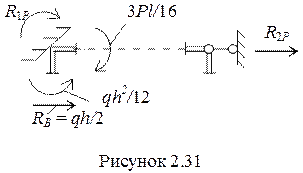
Грузовые коэффициенты определим по эпюре Мр. Вырежем узел с наложенной заделкой и рассмотрим действующие на нее моменты (рисунок 2.31). Реакция R1Р, возникающая в виде реактивного момента в заделке из условий равновесия будет
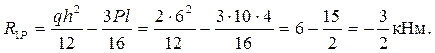
Минус у реакции R1P означает, реакция направлена в сторону, обратную первому единичному воздействию.
Реакция R2Р, возникающая в веденной опоре правого узла, равна верхней реакции в стойке от действия распределенной нагрузки (RВ).
Σх = 0. R2Р = – RВ = – 6 кН.
Знак минус означает, что реакция направлена в сторону, обратную линейному смещению z2.
Запишем систему канонических уравнений с учетом полученных коэффициентов и свободных членов.
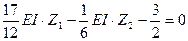
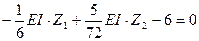
5 Решая записанную систему уравнений, получим
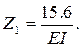
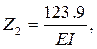
6 Построение окончательной эпюры изгибающих моментов для заданной системы производим на основании принципа независимости действия сил по формуле
M = 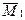 Z1 +
Z1 + 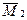 Z2 + Mp,
Z2 + Mp,
т. е. путем сложения эпюр от неизвестных (рисунок 2.32) и грузовой эпюры (рисунок 2.27). Эпюры от неизвестных получаются путем умножения единичных эпюр на значения соответствующих Zi.
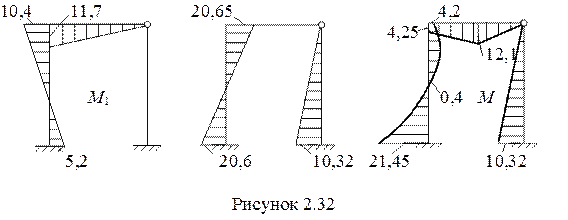
7 Для проверки правильности построения эпюры М производим статическую и деформационную проверки.
Для статической проверки, как и в методе сил, вырезаются незакрепленные жесткие узлы из эпюры М, прикладываются действующие в нем изгибающие моменты и проверяется выполнение уравнения Sm = 0. В нашем случае разность моментов в узле В равна 0,05 кНм, что составляет 1,2%.
|
Деформационная проверка проводится с применение метода сил и заключается в определении перемещений тех сечений, чье перемещение исключено. Так, если выбрать основную систему метода сил с использованием шарнирных узлов в опоре А и в узле В, то угол поворота сечения А должен быть равен нулю, поскольку в заданной системе в точке А жесткая опора.
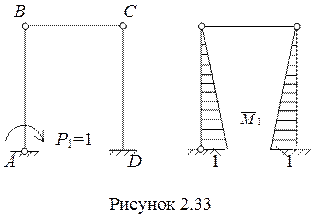
Для его вычисления создадим единичное состояние метода сил (рисунок 2.33), построим единичную эпюру от единичного момента и перемножим результирующую эпюру на единичную.
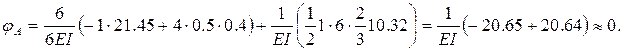
8 Построение эпюр Q и N.
Как и в методе сил, эпюры поперечных сил строятся с использованием формулы графического дифференцирования эпюры моментов
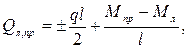
а эпюра продольных сил строится путем рассмотрения равновесия узлов рамы.
В нашем примере:
Левая стойка. 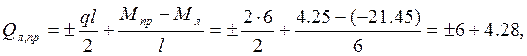
Qл = 10,28 кН, Qпр = – 1,72 кН.
Поперечная сила меняет знак, следовательно, момент в пролете будет иметь экстремум.
Левая часть ригеля 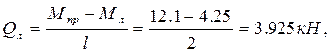
Правая часть ригеля 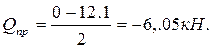
Правая стойка 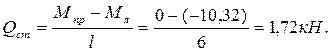
Строим эпюру Q (рисунок 2.34,а).
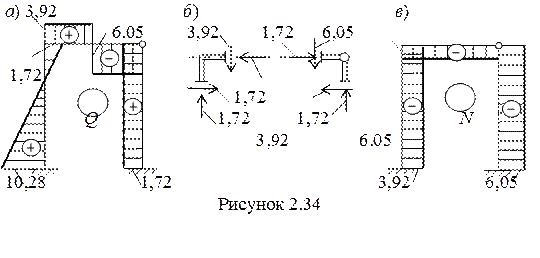
Вырезая левый и правый узлы рамы и рассматривая их равновесие (рисунок 2.34,б), находим продольные усилия в стойках и ригеле и строим эпюру продольных сил N (рисунок 2.34,в).
|
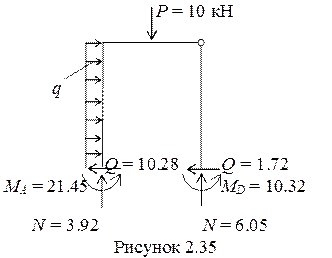
9 В заключение, проводим статическую проверку по аналогии со статической проверкой в методе сил. Отсекаем раму от всех опор и прикладываем в местах отсечений силовые факторы (реакции) по эпюрам M, Q, N (рисунок 2.35).
Должны выполняться все три уравнения равновесия.
Sx = 0, q∙6 – 10.28 – 1.72 = 12 – 12 =0.
Sy = 0, - P + 3.925 + 6.05 = 10 – 9.975 = 0,025 ≈ 0.
Погрешность d = 0.025∙100/10 = 0.25%
SmA = 0, - P∙2 - q∙6∙3 + MA + MD + ND∙ 4 = - 20 – 36 + 21.45 + 10.32 +24.2 =
= 55.97 – 56 = 0.03 ≈ 0.
Погрешность d = 0,03∙100/56 = 0,05%. Т. е. равновесие рамы обеспечено с допустимой погрешностью.
Ниже приводятся задачи по определению внутренних усилий в статически неопределимых системах методом перемещений.


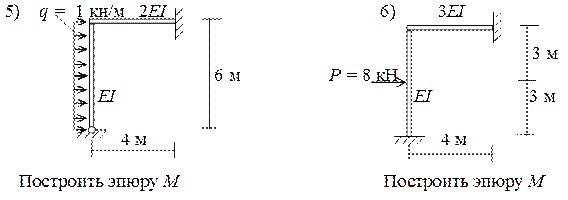
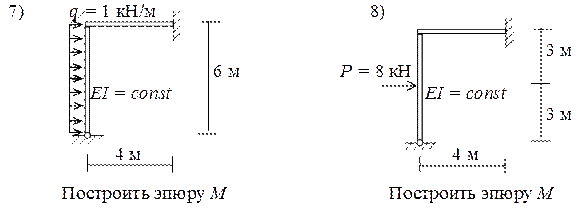
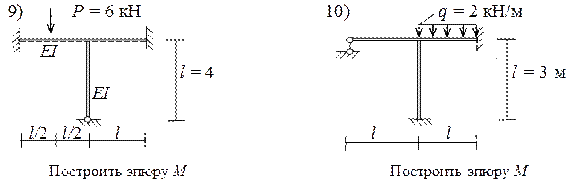
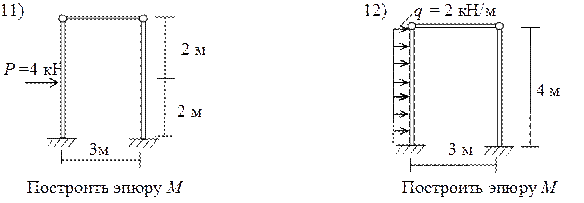
Дата добавления: 2017-02-13; просмотров: 10948;











