ВОЗМОЖНОСТЬ УЧЕТА МНОГОКРАТНОГО РАССЕЯНИЯ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ БИОСРЕДОЙ. ПОНЯТИЕ О ФЕЙНМАНОВСКИХ ДИАГРАММАХ.

Рассмотрение рассеянного биосредой поля квазимонохроматической волны в приближении Кирхгофа, позволяющее представить среду как совокупность случайно отражающих поверхностей, оставляет за рамками учет более чем однократно рассеянного излучения. Во многих задачах лазерной диагностики это допустимо, особенно тогда, когда просвечивается ограниченный слой биосреды (итерационный процесс можно замкнуть). Однако обширный класс задач, рассматривающих неопределенную толщину биосреды, не допускает пренебрежения многократным рассеянием. Это сразу резко усложняет всю вычислительную процедуру и обостряет проблему корректности принимаемых допущений. Но, как и в других статистических задачах, оказывается возможным учет многократного рассеяния не через уменьшение толщины слоя, а вроде бы через самое неразумное предположение – о безграничности рассеивающей среды. Библейский опыт царя Давида работает!

Рассмотрим вначале усредненное поле точечного источника. Поле такого источника, представляющее собой известную по предыдущим главам функцию Грина, удовлетворяет уравнению Гельмгольца:

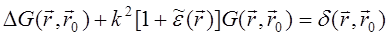(30.1)

Здесь 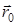— точка нахождения источника, 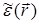— случайная функция. Положив

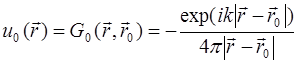, (30.2)

запишем борновский ряд теории возмущений:

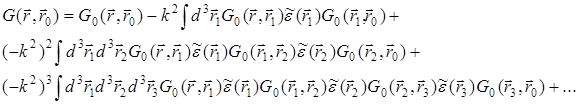(30.3)

Функция Грина, очевидно, симметрична: 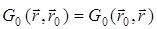. Используя эту симметрию, нетрудно показать, что таким же свойством обладает и функция 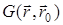— для этого достаточно проделать поочередную замену в интегралах в (30.3). Тем самым имеем теорему взаимности: в произвольной линейной неоднородной среде поле не меняется, если точку расположения источника и точку наблюдения поменять местами.

Проделаем в (30.3) операцию усреднения. Предположив, что случайное поле 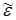гауссово, получим для всех нечетных моментов 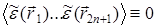, а для четных моментов справедливо соотношение:

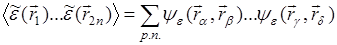(30.4)

где p.n. под знаком суммы означает, что суммирование производится по всем возможным разбиениям индексов 1,2,…n на пары. Например, для n = 2 имеем:

,

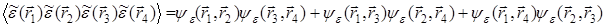а в формуле для данного n будет (2n-1)!!слагаемых. Соотношение (30.4) отражает фундаментальное свойство гауссовых случайных величин, любые четные моменты которых расцепляются на моменты не выше второго порядка. В принципе 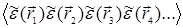можно, как и 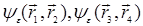и т.д. называть корреляционными функциями, но, имея в виду, что это наименование относят зачастую исключительно к моментам второго порядка, вводится специальный термин кумулянтные функции.

Усредняя (30.3) с учетом (30.4), получим:

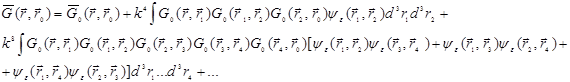(30.5)

Ряд (30.5) требует немалого терпения, чтобы выписать хотя бы первые два члена. На память приходит аналогия с высшей алгеброй, где в свое время шли яростные споры между сторонниками и противниками векторной формы записи необходимых уравнений. К наиболее авторитетным противникам векторов относился знаменитый лорд Кельвин. Он говорил: «Записав уравнение для любой координаты, я могу получить все остальные простой заменой букв. Расходуется при этом только бумага и чернила или мел. А векторное исчисление заставляет применять совершенно излишние умственные усилия. Экономьте же мозги и расходуйте мел. Его не жалко!». Многие современники безусловно соглашались с Кельвином, подпадая под влияние его авторитета. Но не все! Молодой итальянский математик Леви-Чивита в общем соглашался с Кельвином, что векторы — это плохо. Но плохо не потому, что заставляют расходовать мозги. Ведь вместе с мелом по Кельвину расходуется несравненно более ценная и, главное, невосполнимая субстанция — время. А в таком разрезе «экономия мозгов» оборачивается расходом не просто мела. Великий Кельвин либо не очень разбирался в диалектике — на предмет перехода количества времени в качество умозаключений, — либо просто лукавил, имея в виду, что он-то уже достиг вершины научного Олимпа, а те, кто будет «экономить мозги» по его совету, не успеют за свою активную умственную жизнь и приблизиться к подножию оного. Поэтому — да, векторы — это плохо, потому что мало экономят время. И молодой итальянский математик предложил еще больший «расход мозгов» — тензорное исчисление, без которого не появились бы на свет ни теория относительности, ни квантовая механика, ни современная физика твердого тела, ни многие другие области знания, где требуется максимальная концентрация информации в минимальной символике. И вот, примерно лет сорок спустя после создания тензорного исчисления, на ряды типа борновского с тоской взирал молодой американский физик Фейнман, который — один из особо избранных! — получил право участия в знаменитом Манхэттенском проекте. Здесь фактор времени носил вовсе не субъективный, а очень даже объективный характер. От результатов расчетов рассеяния релятивистских частиц зависела реалия создания ядерного оружия. А пока запишешь хотя бы один член борновского ряда, на тебя, того и гляди, обрушится или новый Пирл-Харбор, или, того хуже, успеют состряпать атомную бомбу где-нибудь в Германии. И Фейнман придумал графическое представление элементов борновского ряда, позволяющее экономить время и силы не хуже, чем в свое время тензоры Леви-Чивита. Такого рода графики, или диаграммы, предложенные Фейнманом для решения задач квантовой электродинамики, получили затем распространения в самых различных областях теоретической физики. Они так и называются — фейнмановские диаграммы.

Поставим в соответствие функции Грина 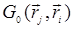отрезок прямой линии, концам которой приписываются координаты :

~ .

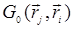Множителю 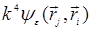сопоставим пунктирную линию с двумя точками на концах:

ri

rj

~

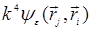Точки 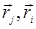, в которых сходятся линии, изображающие G₀ и y_e , будем называть вершинами диаграммы. Условимся, что по координатам всех внутренних вершин производится интегрирование. Число таких вершин будем называть порядком диаграммы.

Приведенные правила соответствия позволяют сопоставить каждому члену ряда (30.5) диаграмму Фейнмана. Так, первый член в правой части (30.5) изображается диаграммой

а второму члену этой формулы соответствует график

Заметим, что, поскольку по координатам внутренних вершин производится интегрирование, аналитическое выражение, изображаемое диаграммой, не зависит от координат внутренних вершин. В связи с этим в дальнейшем не будем отмечать эти вершины на диаграммах. Третьему слагаемому в (30.5) соответствуют три диаграммы:

		r r0		r r0

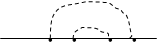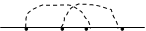Неусредненный член порядка 2n теории возмущений для G имеет вид:

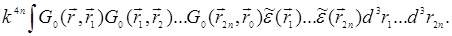
Поэтому диаграммы порядка 2n содержат 2n+1 линий функций Грина G₀ и 2n внутренних вершин r₁…r_2n. Так как при усреднении множитель 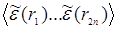распадается на сумму (2n-1)!! cлагаемых, в которых аргументы r₁…r_2n объединяются попарно всеми возможными способами, при усреднении возникает (2n-1)!! диаграмм порядка 2n , в которых 2n вершин соединяются между собой попарно пунктирными линиями всеми возможными способами. Наконец, введем графическое изображение для самой средней функции Грина в неоднородной среде:

r r0

~

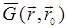Тогда ряд (30.5) можно представить графически следующим образом:

1 2 3 4

= + + + +

+ + + +

	5 6 7 8

9 10 11 12

+ + + +

+ + + + +

	13 14 15 16

17 18 19 20

+ + + + + …

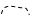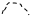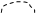
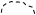
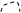
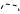
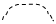
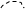
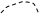
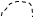
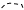
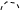
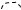
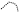
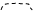
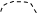
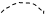
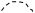
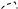
(30.6)

Здесь, помимо записанных в (30.5) членов, представлены еще все 15 членов шестого порядка (диаграммы с 6 вершинами).

Соответствие между диаграммами Фейнмана и аналитическими выражениями является взаимно однозначным. Можно с успехом восстановить по диаграмме аналитическую форму записи. Например, диаграмме 19 из (30.6) соответствует член ряда 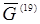, равный

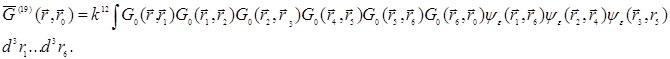(30.7)

Некоторые из диаграмм, входящих в (30.6), содержат в качестве фрагментов диаграммы более низкого порядка. Например, диаграмма 3 содержит в качестве фрагмента диаграмму 2, диаграмма 19 – диаграмму 4 и т.д. Этим можно воспользоваться для сокращения аналитических выражений. Например, можно записать (30.7) в виде:

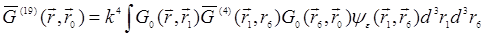(30.8)

где

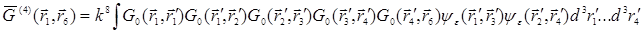
(30.9)

Нетрудно убедиться, что подстановка (30.9) в (30.8) дает после изменения обозначений переменных интегрирования (30.7).

Дадим физическую интерпретацию диаграмм Фейнмана. Диаграмма 1 из (30.6) описывает распространение волн из точки r₀ в точку r без рассеяния (как в однородной среде). Диаграмма 2 описывает следующий процесс: волна распространяется, как в однородной среде, из точки r₀ в точку r₂ . Здесь происходит первое рассеяние, после чего рассеянная волна распространяется в точку r₁ , где происходит второе рассеяние. Двукратно рассеянная волна достигает точки наблюдения r. Распространение описывается множителями

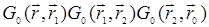. Наличие в диаграмме 2 корреляционной функции 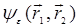указывает на то, что оба рассеивателя (в точках 1 и 2) коррелированы, т.е. оба рассеяния фактически произошли на одной и той же неоднородности.

Обратимся теперь к диаграммам второго порядка, т.е. диаграммам 3-5. Все они содержат одно и то же произведение 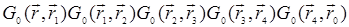. Это значит, что волна в точку r пришла после рассеяния в точке r₁ , в точку r₁ – после рассеяния в точке r₂ и т.д. Первому рассеянию в точке r₄ подвергалась первичная волна 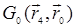. Таким образом, все эти диаграммы описывают четырехкратное рассеяние. В чем же разница между процессами, которые описываются этими топологически различными диаграммами? В диаграмме 3 линии корреляционных функций соединяют точку r₁ с r₂ и точку r₃ с r₄. Это означает, что обе точки r₁ и r₂ принадлежат одной неоднородности, r₃ и r₄ – другой. Таким образом, процесс, описываемый диаграммой 3, заключается в том, что сначала происходит свободное распространение волны от источника к первой неоднородности, затем двукратное рассеяние на ней, затем – свободное распространение двукратно рассеянной волны до второй неоднородности, после чего – двукратное рассеяние на второй неоднородности. На рис. 30.1 схематически показана последовательность рассеяний на двух неоднородностях в соответствии с топологией диаграмм 3,4 и 5.

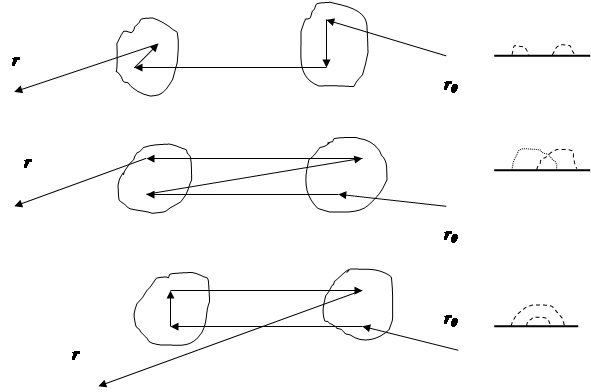Рис. 30.1.

Четырехкратное рассеяние на двух неоднородностях в

соответствии с топологией фейнмановских диаграмм

Представление решения уравнения (30.1) в виде совокупности диаграмм (30.6) полезно не только из-за наглядности, но и потому, что оно позволяет преобразовывать ряд теории возмущений, используя топологические признаки входящих в решение диаграмм. При этом удается выразить сумму ряда (30.5) через сумму некоторой бесконечной подпоследовательности этого же ряда. Чтобы осуществить такую операцию, произведем сначала классификацию входящих в (30.6) диаграмм.

Назовем входящую в 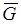диаграмму слабо связной, если ее можно разделить на две отдельные диаграммы, разорвав какую-либо одну линию G₀ . В формуле (30.6) такими являются диаграммы 3, 6-9 и 12. Остальные диаграммы назовем сильно связными (2,4,5,10,11, 13-20 в (30.6)). Диаграммы, получающиеся из слабо связной диаграммы путем разрыва линий G₀, в свою очередь могут оказаться сильно или слабо связными. Если среди «вторичных» диаграмм есть слабо связные, то и их можно путем разрыва какой-либо сплошной линии разбить на более простые диаграммы. Продолжая этот процесс, придем в конечном счете к некоторому количеству сильно связных диаграмм. Назовем число сильно связных диаграмм, на которое может быть разбита слабо связная диаграмма, показателем связности исходной диаграммы. Возвращаясь к формуле (30.6), можно сказать, что диаграммы 3,7-9 и 12 имеют показатель связности 2, а диаграмма 6 — показатель связности 3. Сильно связным диаграммам припишем показатель связности 1.

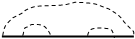
Отберем из ряда (30.6) все сильно связные диаграммы. Так как каждая из диаграмм начинается и оканчивается линией G₀, сумму всех сильно связных диаграмм можно представить в виде

(30.10)

где введено обозначение

=

+ + +

+ + + +

+ + + +

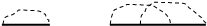
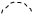
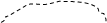
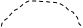
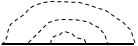+ + … (30.11)

В аналитической форме (30.10) имеет вид

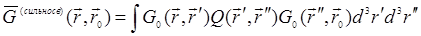(30.10а)

где

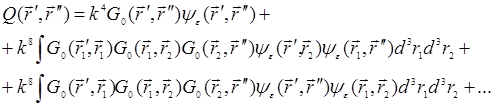(30.11а)

Функция Q носит название ядра массового оператора (пришло из квантовой теории поля).