Вычислительная обработка теодолитных ходов

Вычислительная обработка теодолитных ходов (и полигонов) необходима для получения координат точек этих ходов. Чем больше теодолитных ходов и полигонов обрабатывается совместно, тем сложнее вычисления. Чтобы правильно выбрать последовательность вычислительных действий, составляют схематический чертёж всех ходов, записывают на нём измеренные значения горизонтальных углов, длин линий, особо отмечают пункты геодезической сети с уже имеющимися координатами. Сложность вычислительного процесса обязывает проверить все вычисления: углов в полуприёмах, средних значений углов в полном приёме, средних длин линий. Если не произвести этих проверок, то нередко ошибки полевых вычислений вскрываются уже после полной обработки ходов, что заставляет исполнителя переделывать всю работу заново. Поэтому на проверку полевых вычислений обращается самое серьёзное внимание и предъявляется требование выписывать чернилами средние значения углов в графе 5 полевого журнала (табл 6).

Если полигон привязан к пунктам геодезической сети, то прежде всего производят вычисления координат одной точки полигона, привязанной к пункту геодезической сети и дирекционного угла первой из привязываемых сторон полигона. Поэтому на схематическом чертеже изображают пункты геодезической сети, к которым полигон привязан, линии привязки, записывают исходные дирекционные углы, координаты пунктов геодезической сети, примычные углы (рис.95) горизонтальные проложения, измеренные при привязке полигона.

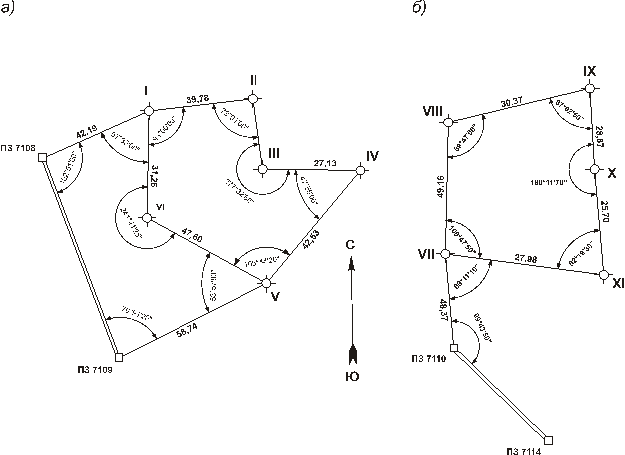
Рис.95

Схематический чертёж теодолитных ходов с выписанными на нём значениями измеренных углов и длин необходим для вычисления угловых невязок. Например, в многоугольнике (полигоне) сумма углов должна равняться 180° (n-2), где n- число углов. В действительности, вследствие ошибок в измерениях сумма измеренных углов оказывается больше или меньше этой теоретической суммы.

Разность между суммой измеренных углов и теоретической суммой называется угловой невязкой.

Одна из задач вычислительной обработки результатов измерений- распределить невязку на отдельные измерения, т.е. ввести в них поправки по определённым математическим правилам. Процесс распределения невязки называется увязкой (уравниванием). После уравнивания полученные исправленные значения углов будут удовлетворять определённым геометрическим условиям, как, например, сумма увязанных углов должна равняться теоретической сумме.

Все вычисления при обработке теодолитных ходов производятся в так называемых «Ведомостях вычисления координат» [11], которая заполняется в такой последовательности (табл.12):

1. Угловая увязка теодолитного хода (полигона).

Проверив правильность вычисления углов в журнале измерений, значения углов в полигоне выписывают в графу 2 «Ведомости вычисления координат» (табл.12) по порядку в направлении хода часовой стрелки; вычисляют практическую сумму углов и записывают её в этой же графе (2).

Подсчитав практическую сумму углов полигона и теоретическую сумму, вычисляют угловую невязку (fb) по формуле:

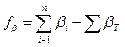(138)

где 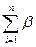- сумма измеренных углов (практическая сумма);

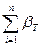- теоретическая сумма углов.

Теоретическая сумма углов вычисляется по формулам:

а) для замкнутого полигона

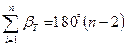(139)

где n-число углов в полигоне;

б) для разомкнутого хода, для правых углов

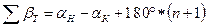(140)

в) для разомкнутого хода, для левых по ходу углов

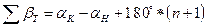(141)

где aН и aК- дирекционные углы начальной и конечной сторон хода;

n- число сторон хода.

Невязку, полученную по формуле (138), сравнивают с допустимой

(fbдоп.):

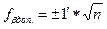(142)

где n- число углов в ходе

Таблица 12

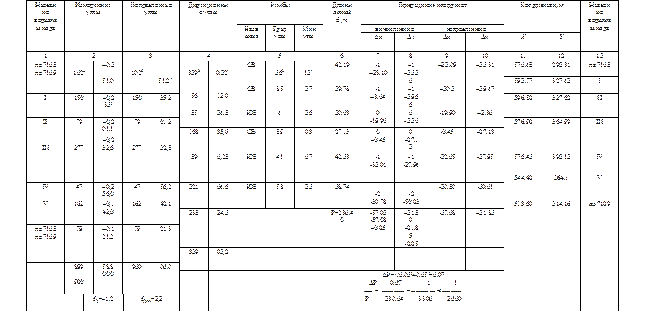
Если угловая невязка получилась больше допустимой, надо второй раз проверить вычисление углов в полевом журнале. Если ошибка в расчётах не обнаружена, значит имеется ошибка в полевых измерениях, которые надо произвести вновь.

Если угловая невязка меньше допустимой, то её распределяют с обратным знаком на все углы поровну. Поправку db вычисляют по формуле:

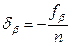(143)

где n- количество углов.

Если fb не делится без остатка на n, то большую по абсолютной величине поправку вводят в углы с короткими сторонами.

В теодолитных ходах небольшой длины поправки в измеренные углы можно вводить так, чтобы углы были округлёнными до минут. Значения поправки записывают в графу 2 над значением минут.

Для контроля подсчитывают сумму поправок, она должна равняться невязке с обратным знаком.

Вычисляют исправленные углы по формуле:

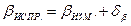(144)

и значения записывают в графу 3. Сумма исправленных углов должна равняться теоретической.

2.Вычисление дирекционных углов (a) сторон полигона ведут по формулам в зависимости от того, какие по ходу измерялись углы (b) правые или левые.

Пусть в теодолитном ходе 1-2...n (рис. 96)

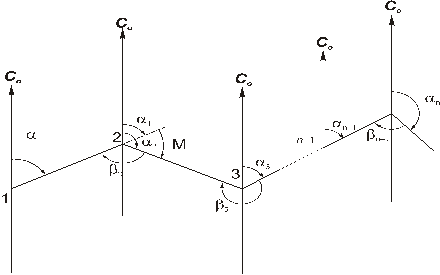
Рис. 96

Измерены правые по ходу углы (b1,b2,...bn-1), а дирекционный угол начальной стороны (a1) известен из привязки, тогда дирекционный угол следующей стороны (a2) будет равен (рис.96):

a2= a1+M (145)

М=180°-b1 (146)

Подставим 146 в 145, получим:

a2= a1+180°-b1 (147)

В общем виде формулу 147 можно записать:

an= an-1+180°-bn (148)

Для измеренных левых по ходу углов вычисление дирекционных углов ведут по формуле:

an= an-1+bn-180° (149)

Здесь anи an-1 - дирекционные углы следующей и предыдущей сторон хода.

Румбы (r) сторон теодолитного хода находят по зависимостям, выраженными в табл. 3.

Вычисление дирекционных углов начинают с дирекционного угла начальной стороны, в рассматриваемом примере это сторона ПЗ 7108-I (ПЗ-полигонометрический знак), в такой последовательности:

ПЗ 7109-7108 + 339°03¢, 2

180°00

- 519°03¢, 2

102°51¢, 2

- 416° 12¢, 0

360° 00

a:ПЗ 7108-1 + 56° 12¢,0

180° 00

- 236° 12¢,0

150° 35¢, 2

a: I-II + 75° 36¢, 8

180° 00

- 265° 36¢, 8

79° 01¢, 2

a:II-III +186° 35¢, 6

180° 00

- 366° 35¢, 6

277° 32¢, 8

a:III-IV + 89°02¢, 8

180° 00

- 269° 02¢, 8

47° 56¢, 2

a:IV-V + 221° 06¢ , 6

180° 00

- 401° 06¢ , 6

162° 42¢ , 1

a:V-ПЗ 7109 + 238° 24¢, 5

180° 00

- 418° 24¢, 5

79° 21¢, 3

a:П37109-7108 339° 03¢, 2

Дирекционный угол исходной стороны (ПЗ 7109- ПЗ 7108)- 339°03¢,2 был получен из решения обратной геодезической задачи поизвестным координатам полигонометрических знаков (ПЗ) №7109 и №7108.

Сущность обратной геодезической задачи состоит в том, что по известным координатам двух точек определяется дирекционный угол линии, соединяющей эти точки и расстояние (горизонтальное проложение) этой линии (рис.97).

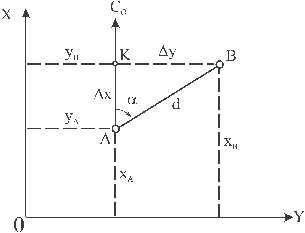
Рис.97

Из прямоугольного треугольника АКВ, дирекционный угол линии АВ найдём:

tg aАВ= Δy/ Δx =( yВ-yA)/ (xB-xB) (150)

aAB= arc tg (Δy/ Δx) (151)

Горизонтальное проложение (dAB) линии АВ запишем:

dAB= Δy / sinaAB (152)

Для контроля вычислим:

dAB=Δx/ cosaAB (153)

Расхождение в расстоянии, вычисленном по формулам 152 и 153 не должно превышать 2 см; если это условие не будет выполнено, расчёты, начиная с формулы 150 и кончая формулой 153 повторяют.

Точки А и В (рис.97), как правило, являются пунктами государственной геодезической сети или пунктами сетей сгущения. К ним производится привязка теодолитных ходов и при этом решается обратная геодезическая задача.

Контролем правильности вычислений дирекционных углов в полигоне служит равенство вычисленного конечного дирекционного угла через сторону V- ПЗ7109 и исходного значения дирекционного угла, заданного вначале (339°03׳,2). Если контроль сошёлся, вычисленные значения дирекционных углов записывают в графе 4 табл.12.

Вычисляют румбы сторон теодолитного хода в соответствии с табл.3, результаты записывают в графе 5.

Например, румб линии II-III равен:

r3= ЮЗ*(186° 36׳ - 180°) =ЮЗ: 6°36׳

Вычисляют горизонтальные проложения сторон полигона по формуле 63, результаты записывают в графе 6 и подсчитывается длина хода, т.е. периметр (P).

3. Вычисление приращений координат и линейная увязка полигона.

Приращения координат сторон теодолитного хода находятся по формулам прямой геодезической задачи, сущность которой заключается в определении координат следующей точки, если известны координаты предыдущей, горизонтальное проложение между точками и дирекционный угол стороны (рис.98).

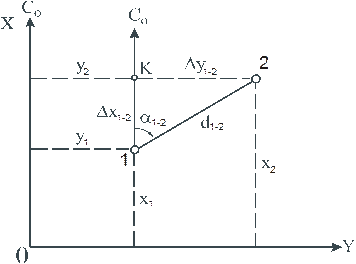
Рис. 98

В прямоугольном треугольнике катеты 1К и2К, обозначенные, как приращения координат, находятся по формулам:

Δx1-2= d1-2*cosa1-2(154)

Δy1-2= d1-2*sina1-2(155)

Из рис. 98 видно, что координаты точки 2 будут равны:

x2= x1+Δx1-2 (156)

y2= y1+ Δy1-2 (157)

При привязке теодолитного хода к опорным геодезическим пунктам (ПЗ 7108, ПЗ 7109 в рассматриваемом примере) необходимо знать дирекционный угол исходной стороны, который находится из решения обратной геодезической задачи.

Приращения координат вычисляют с помощью калькулятора или с помощью «Таблиц приращений координат», результаты записывают в графы 7 и 8 (табл.12)

Например, приращения координат линии II-III через дирекционный угол будут равны:

ΔxII-III=dII-III*cosaII-III = 20,03м*cos 186° 35׳,6 = -19,90м.

ΔyII-III= dII-III*sinII-III= 20,03м*sin 186° 35׳,6 = -2,30м.

через румбы:

ΔxII-III=dII-III*cos rII-III= 20,03м*cos 6° 36׳= -19,9 м.

ΔyII-III= dII-III*sin rII-III = 20,03м*sin6° 36׳= -2,30м.

Знаки у приращений координат определяются в зависимости от четверти, в которой расположена линия хода или в зависимости от названия румба линии по рисунку 99.

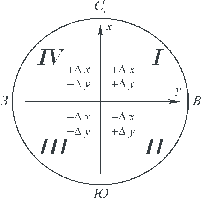
Рис.99

В замкнутом полигоне теоретически сумма приращений по оси x (SDx ) и сумма приращений по оси y (SDy) должна быть равна нулю. Но ввиду появления случайных ошибок измерения длин линий и углов в полигоне, а также ввиду ошибок вычислений, возникают отклонения от нуля, т.е. появляются невязки (fx, fy) по осям x и y, которые находятся по формулам:

fx= S Dx (158)

fy= S Dy (159)

В разомкнутом полигоне, опирающемся на пункты геодезической сети, невязки находят по формулам:

fx= S Dxn- S DxТ (160)

fy=S Dyn - S DyТ (161)

где S Dxn, S Dyn - практическая сумма приращений координат в теодолитном ходе (суммы в столбцах 7,8 табл.12);

S DxТ, S DyТ- теоретическая сумма приращений координат.

Теоретические суммы приращений координат находят по формулам:

S DxТ= XK- XН (162)

S DyТ= YК– YН (163)

где XK, YК и XН, YН- соответственно координаты конечной и начальной точек теодолитного хода (ПЗ 7108 и ПЗ 7109 применительно к рассматриваемому примеру с координатами в гр.11,12 табл.12).

Вычислив линейные невязки по формулам 158, 159 (если замкнутый полигон) или по формулам 160, 161 (если полигон разомкнутый), производят оценку величин полученных невязок, для чего сначала вычисляют абсолютную невязку (fабс.) по формуле:

fабс.= 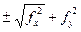(164)

Абсолютная невязка (ошибка) не даёт представления о точности измерений. За критерий точности измерений принимается относительная невязка (fотн.), вычисляемая как:

fотн.= 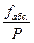(165)

где P- периметр хода (сумма длин сторон теодолитного хода, графа 6 (табл. 12).

Допустимая невязка не должна превосходить известного предела, устанавливаемого Техническими инструкциями. Так, для теодолитных ходов, относительная невязка не должна превышать:

fотн. 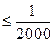(166)

Если после расчётов относительной ошибки условие формулы (166) соблюдается, то невязки по осям fxи fyраспределяют с обратным знаком на все приращения координат пропорционально длинам горизонтальных проложений. Поправки в приращения координат вычисляют по формулам:

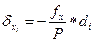(167)

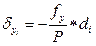(168)

Применительно к рассматриваемому полигону невязка по оси x составляет +0.05м, невязка по оси y-0.05м, периметр 230,4м.

Рассмотрим пример вычисления поправок по формулам (167, 168) для приращений линии V-ПЗ 7109:

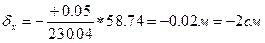
Вычисленные поправки в сантиметрах подписываются над соответствующими приращениями координат (графы 7,8 табл.12).

Контролем правильности распределения невязок должно быть:

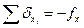
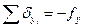(169)

Вычисляют исправленные приращения координат (Dxиспр. и Dyиспр.) по формулам:

Dxi испр.= Dxi выч.+dx i (170)

Dyi испр.= Dyi выч. +dy i (171)

то есть производится алгебраическое сложение вычисленного приращения с поправкой. Исправленные приращения координат записывают в графы (8,9) табл.12. Контролем вычислений должно быть:

Dxi испр.= Dxтеор.

Dyi испр.=Dyтеор.

(Для замкнутого полигона должно быть: Dxиспр.=0 , Dyтеор.=0)

4. Вычисляют координаты вершин теодолитного хода по формулам:

Xi=Xi-1+Di испр. (172)

Yi=Yi-1+Di испр. (173)

где Xi-1, Yi-1и Xi, Yi- координаты предыдущей и последующей точек теодолитного хода.

Например,

xI = x7108+Dxиспр. = 570,68+23,09 = 593,77

yI = y7108+Dyиспр.= 292,31+35,31 = 327,62

и т.д. Контролем правильности вычислений координат служит совпадение вычисленных координат конечной точки с заданными координатами этой же точки. В рассматриваемом примере (табл.12)

это координаты ПЗ 7109.

Аналогично вычисляют координаты точек диагонального хода (рис.95а). Образец обработки приведён в таблице 13 [11].

Таблица 13

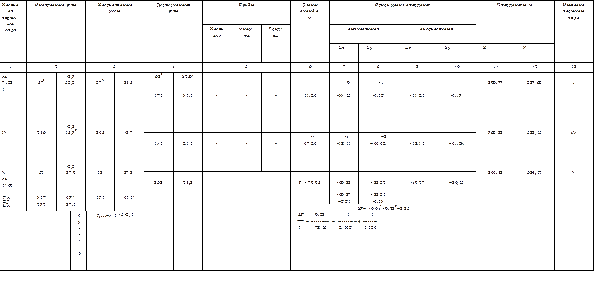
§ 35.2 Обработка материалов нивелирования точек теодолитного хода

Поскольку теодолитная съёмка является горизонтальной и она не даёт представления о рельефе на территории съёмки, то для устранения этого недостатка производится геометрическое нивелирование точек теодолитного ( и диагонального) хода. Таким образом создаётся высотное обоснование, с которого впоследствии ведётся тахеометрическая съёмка.

В табл.14 привелён фрагмент «Журнала технического нивелирования» точек теодолитного хода от полигонометрического знака №7108, отметка которого известна (гр.6 в табл.15)

Таблица 14

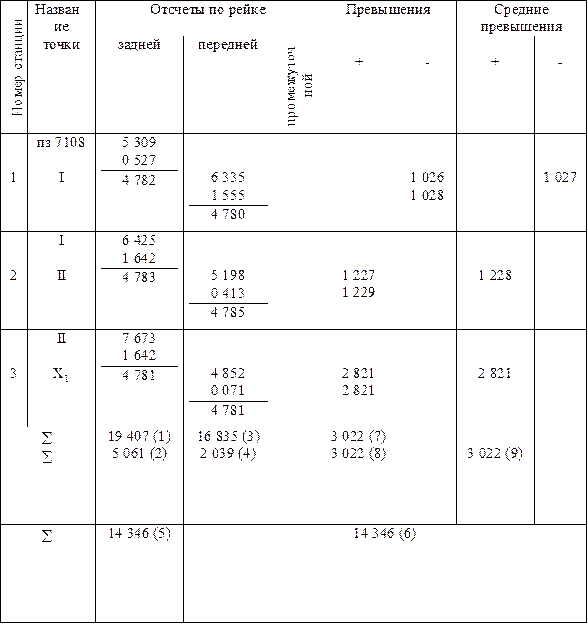
Порядок обработки (фрагмент) “Журнала” (вычисление превышений и средних превышений) приведён в табл.7.

Опишем подробнее обработку «Журнала технического нивелирования» (табл. 14), последовательность действий в ней обозначена цифрами в способах:

1. Выполняют постраничный контроль, т.е. подсчитывают сумму «красных» отсчётов по задним рейкам (S19407) и сумму «чёрных» отсчётов (S5061) и находят разность между ними (S14346). Аналогично находят суммы отсчётов по передним рейкам и окончательную разность (S14346), которая должна быть такой же как и по задним рейкам; сравнивают разности (1) - (2) и (3) - (4) с суммами разностей нулей реек (5) и (6). Расхождения в 1мм и более свидетельствует о наличии ошибок в вычислениях.

Далее подсчитывают суммы (7) и (8) положительных и отрицательных превышений и осуществляют контроль: (1) - (3) = (7) и (2) - (4) = 8. Затем вычисляют сумму (9) - средних значений превышений. Среднее значение из величин (7) и (8) не должно отличаться от величины (9) более чем на 1 мм.

В журнале технического нивелирования составляют схему высотного обоснования, на которой показывают исходные пункты (красным цветом), точки обоснования, выписывают средние превышения между ними и стрелкой показывают направление хода. Образец схемы показан на рис.100

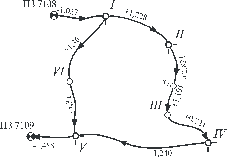
Рис.100

Вычисления отметок точек съёмочного обоснования производят в специальной “Ведомости” (табл.15).

В “Ведомость” из журнала технического нивелирования выписывают превышения, число штативов (количество установок нивелира между точками при сложном нивелировании), подсчитывают сумму превышений и вычисляют невязки для замкнутого полигона по формуле:

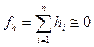(174)

где hi - превышение в полигоне. Для разомкнутого полигона:

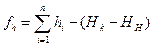(175)

или

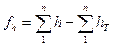(176)

где H_H и H_K -отметки начальной и конечной точек привязки, а разность их есть S hT - теоретическая сумма превышений нивелирного хода (ПЗ7109, I, II,.. ПЗ7108).

Таблица 15

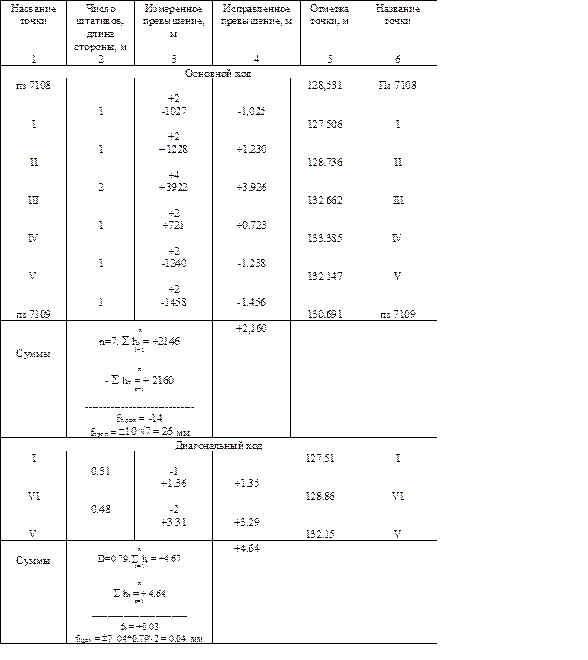
Невязки распределяют, как правило, поровну на все превышения (или пропорционально числу станций) и выписывают их величины в милимметрах над значениями превышений. Для контроля правильности распределения подсчитывают сумму поправок. Она должна равняться невязке с обратным знаком.

Далее вычисляют исправленные значения превышений и записывают их в графе 4 табл.15, в графе 5 записывают красным цветом исходные отметки (начальной и конечной точек хода). Отметку каждой точки вычисляют по формуле:

Hi+1= Hi+ hi׳ (177)

где Hi+1 и Hi - отметки последующей и предшествующей точек;

hi׳ - исправленное значение превышения между точками.

Пример.

HI= HПЗ7108+ h1׳

HI= 128,531 + (-1,025) = 127,506

HII= HI+ h2׳

и т.д.

H7109= HV+ h6 (178)

Контроль: вычисленная высота по ф. 178 и исходная (130,691 гр.5 табл.15) отметка конечной точки должны совпадать.

При обработке диагонального хода (I-VI-V рис.95) в графу 3 табл.15 выписывают из журнала измерений превышения в метрах; из ведомости вычислений координат (табл.12) - длины сторон в сотнях метров; подсчитывают сумму превышений по ходу; вычисляют невязку по формуле 188 и сравнивают её с допустимой:

fh доп.= ± 0.04 D√n(179)

где D - длина хода в сотнях метров (0,79);

n - число сторон хода (2);

Если невязка, вычисленная по формуле 188, не превосходит допустимую (179), то её распределяют аналогично описанному выше и вычисляют отметки точек диагонального хода по формуле 177.