Метод тригонометрического нивелирования

Сущность метода заключается в определении превышения между точками с помощью теодолита по формулам тригонометрии.

Пусть на местности закреплены точки А и К, необходимо определить превышение (h) между ними (рис.67).

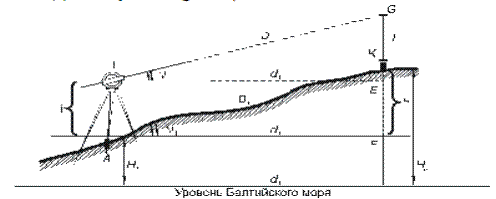
Рис.67

Измеряют наклонное расстояние между точками (Д) и угол (n) наклона линии к горизонту. Горизонтальное проложение (d) линии находят по формуле (71).

Из рис.67 запишем:

h=i+EK(81)

где i - высота инструмента

EK=GE-l (82)

где l - высота наведения оси визирования на вешку

GE=d*tgn (83)

d=D*cosn (84)

Значения Д и Д1,n и n1близки или равны ( если l=i ), поэтому подставим значения 82, 83 и 81 получим:

h=d1*tgn1+i-l (85)

Абсолютная отметка точки К будет равна (рис.67):

HК=HА+h (86)

где НА- абсолютная отметка точки А (известна).

Превышение может быть вычислено через расстояние, измеренное по нитяному дальномеру, используя формулу 71. Подставим её в формулу 85 и запишем:

h= Cn*n cosn*sinn/cosn + i – l

Умножим и разделим на 2 первое слагаемое, сократим на cosn, получим:

h=1/2 C*n*2sinn * cosn+i - l

Введём обозначения синуса двойного угла:

h= 1/2 C*n*sin2n+i – l (87)

Общие сведения из теории ошибок (погрешностей) геодезических измерений

Ошибки и их виды

Измерения в геодезии рассматривают с двух точек зрения: количественной, выражающей числовое значение измеренной величины, и качественной, характеризующей ее точность.

Из практики известно, что даже при самой тщательной и аккуратной работе (многократные) повторные измерения не дают одинаковых результатов.

Этот факт указывает на то, что получаемые результаты не являются точными значениями измеряемой величины, а несколько отличными. Отклонение результата измерения величины от ее истинного значения называется истинной ошибкой (погрешностью).

Величина погрешности характеризуется точностью измерений. Если обозначить истинное значение измеряемой величины через Х , а результат измерения этой же величины через li, то истинная погрешность измерений (Di) определяется из выражения:

Δi=li–Х (88)

Любая погрешность результата измерения есть следствие действия многих факторов, каждый из которых порождает свою погрешность. Изучением свойств и закономерностей действия геодезических ошибок измерений, разработкой методов получения наиболее точного значения измеряемой величины и характеристик, их точности занимается специальная дисциплина “Теория ошибок”. Излагаемые в теории ошибок измерений методы решения задач позволяют рассчитать необходимую точность предстоящих измерений и на основе этих расчетов выбрать соответствующие (по точности) приборы и методику измерений, а после производства измерений получить наилучшие их результаты и оценить их точность . Математической основой теории ошибок измерений являются теория вероятностей и математическая статистика.

Ошибки измерений разделяют по двум признакам: по характеру их действия и по источнику происхождения.

По характеру действия погрешности бывают: грубые, систематические и случайные.

Грубыми называются ошибки, превосходящие по абсолютной величине некоторый, установленный для данных условий измерений предел. Они происходят в большинстве случаев в результате промахов и просчетов исполнителя.

Например, линия измерена в прямом направлении; ее длина составила 148,55м; после измерения линии в обратном направлении результат получился 168,50м. Здесь 20м - грубая ошибка.

Второй пример : горизонтальный угол измерен при КП, результат - 68° 31ў. При измерении этого же угла вторым полуприемом (при КЛ) получилось 67° 30ў . Здесь 1° - грубая ошибка.

Систематические ошибки возникают по определенным причинам и характеризуется постоянством своей величины знака. Причинами их появления могут быть неточности измерительных приборов, личные физиологические особенности наблюдателя, влияние внешних факторов и др. Систематические ошибки, их величина устанавливаются в процессе работы и исключаются из результатов измерений. Примерами систематических ошибок являются: ошибка за компарирование мерного прибора, ошибка за влияние кривизны Земли и рефракции при нивелировании и др.

Случайные погрешности – точный размер и характер влияния которых на каждый отдельный результат измерения остается неизвестным. Величину и знак случайной ошибки заранее установить нельзя. Однако практические и теоретические исследования показывают, что случайные ошибки подчиняются определенным вероятностным закономерностям, изучение которых дает возможность получить наиболее надежный результат и оценить его точность.

По источнику происхождения различают ошибки инструментальные, внешние и личные.

Инструментальные ошибки обусловлены несовершенством измерительных приборов, например, ошибки в угле, измеряемом теодолитом, из-за неточного приведения оси вращения теодолита в отвесное положение.

Внешние ошибки происходят из-за влияния внешней среды, в которой выполняются измерения, например, погрешность в отсчете по нивелирной рейке возникает из-за изменения температуры воздуха на пути луча визирования (рефракция).

Личные ошибки - ошибки, связанные с особенностями наблюдателя.

Учитывая, что грубые ошибки исключаются при повторных измерениях, а систематические ошибки устраняются после их определения, то оценку выполненных измерений производят, по случайным ошибкам основываясь на их свойствах.