Дальномерное определение расстояний

Наиболее распространенным в этом деле является нитяной дальномер с постоянным углом. На рис.61 схематически показан ход лучей в зрительной трубе , проходящих через точки пересечения вертикальной нити сетки с тремя горизонтальными нитями: двумя дальномерными (m,к) и центральной.

Дальномерные нити служат для измерения расстояния с помощью рейки (рис.61б).

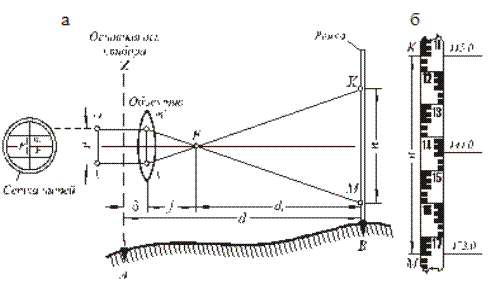
Рис.61

Пусть требуется определить расстояние d от точки А, в которой центрирован теодолит, до точки В, в которой установлена дальномерная рейка. Расстояние от оси вращения инструмента до рейки (рис.61) равно:

d=δ+f+d0 (64)

где d- расстояние от оси вращения инструмента до объектива (величина известная);

f - фокусное расстояние объектива (величина известная).

Для удобства последующего вывода формулы 64 и для упрощения в обозначениях, приведенных на рис.61а, примем следующие расстояния: между дальномерными нитями (mк, m’к’) как р; расстояние по рейке (между проекциями дальномерных нитей) - MK как n - количество делений по рейке; высоты в треугольниках MFK и m’k’f как d0и f соответственно.

Тогда из подобия треугольников MKF и m’k’f запишем:

d0 /f=n/р

d0 =f*n/р (65)

Подставим 65 в 64 получим:

d=f*n/р+d+f (66)

Здесь f/р - величина постоянная, называется коэффициентом дальномера, обозначается буквой С и равна 100

d+f-также постоянная величина, обозначаемая c, составляет порядка 0,3

После этого формулу 66 можно записать в виде:

d=C*n +c (67)

Формула 67 справедлива, когда луч визирования перпендикулярен к рейке (возникает подобие треугольников), т.е.когда местность горизонтальна . В действительности же местность, как правило, является наклонной (рис.62) и тогда отсчет по рейке МК (n) будет увеличен по сравнению с отчетом (n’) между точками M’K’ (как если бы рейка была перпендикулярна оси визирования ). Угол в точке С равен углу n, как углы со взаимно перпендикулярными сторонами ( РРОС и РКСК’), Отсчет по рейке (М’К’) перпендикулярной оси визирования будет равен

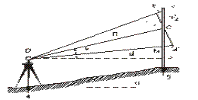
Рис.62

n’=n*cosn (68)

что будет означать, что измеренное расстояние Д (рис.62), которое из ф.67 будет равно:

Д=Сncosn+c (69)

Горизонтальное проложение длины линии измеренной по нитяному дальномеру будет равно:

d=(Cncosn+c)cosn

d=CncosІn+ccosn(70)

B виду того, что “с”- величина малая (0,3м) и еще умноженая на косинус, то вторым слагаемым можно пренебречь и (70) записать:

d=Cn*cosІn (71)