Среднеквадратическая ошибка отдельного измерения и арифметической середины, вычисленные через вероятнейшие ошибки

Истинное значение (Х) измеряемой величины, практически, неизвестно. Значит неизвестны и истинные ошибки (D) измерений и истинная ошибка арифметического среднего (М). За вероятнейшее значение измеряемой величины принимается арифметическое среднее (х) из всех отдельных измерений.

Произведем оценку точности отдельных измерений и арифметической середины, когда истинное значение измеряемой величины неизвестно.

Вычтем из системы равенств (93) систему равенств (92), получим:

Δ1-V1=x-X

Δ2-V2=x-X (108)

................

Δn-Vn=x-X

Перенесем вероятнейшие ошибки из левой части равенств в правую, возведем в квадрат каждое равенство

Δ12=V12+2V1(x-X)+(x-X)2

Δ22=V22+2V2(x-X)+(x-X)2 (109)

...........................................

Δn2=Vn2+2[Vn](x-X)+(x-X)2

В системе 109 значение (х-Х) заменим через М (105,106), сложим левые и правые части, введем обозначение Гаусса и разделим левые и правые части равенства (109) на n, получим:

[Δ2]/n = [V2]/n +2*[v]/n *(x-X) +M2 (110)

В формуле 110 слагаемое 2*[V]/n *(x-X) равно нулю по четвёртому свойству случайных ошибок: слагаемое М2представим как [Δ2]/n2(ф.107), после этого ф.110 запишем:

[Δ2]/n = [V2]/n + [D2]/n2 (111)

Подставим в 111 значение 104 получим:

m2=[V2]/n+m2/n (112)

Решим уравнение (112) относительно m и произведем преобразования:

nm2=[V2]+m2; m2(n-1)=[V2]

m2=[V2]/(n-1) (113)

Извлечем корень квадратный из обеих частей равенства 113, получим

m=±Ц[V2]/(n-1) (114)

Формула 114 называется формулой Бесселя.

Среднеквадратическая ошибка арифметической середины через вероятнейшие ошибки после подстановки 114 в формулу 107 и преобразований будет равна:

М=±Ц([V2]/n(n-1)) (115)

Рассмотрим на конкретных примерах вычисление среднеквадратических ошибок отдельного измерения и арифметического среднего через истинные и вероятнейшие ошибки.

1.Пусть дан ряд из 10 треугольников, составляющих звено триангуляции 4 класса (рис.68)

Рис.68

В каждом треугольнике измерены все три угла b1,b2,b3. Обозначим фактическую сумму трех углов в первом треугольнике как l1, во втором треугольнике – l2и т.д. Истинное значение (Х) суммы углов в треугольнике составляет 180°, тогда истинные случайные ошибки найдем по ф.93 и запишем в табл.8.

Таблица 8

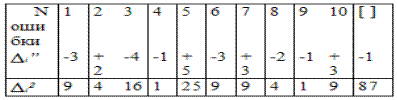
Проверяем четвертое свойство случайных ошибок (89).

Lim[Δ]/n=-1/10=0,1~0

Вычисляем среднеквадратическую ошибку отдельного измерения.

m=±√87/10=±√8,7=±2,9

2. Измерен горизонтальный угол (b) в треугольнике 8-ю приемами (табл.9). Проведем оценку точности измерений и вычисления арифметической середины. Поскольку истинное значение угла неизвестно, вычисляем его вероятнейшее значение (среднеарифметическое) по формуле 90.

Таблица 9

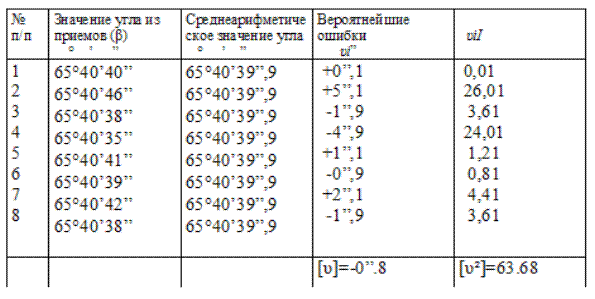
x=65°40’+(40”+46”+38”+35”+41”+39”+42”+38”)/8

x=65°40’+319”/8=65°40’+39”,9

x=65°40’39”,9

Вычисляем вероятнейшие ошибки отдельных измерений (92) и их квадраты , результаты записываем в табл.9:

u1=65°40’40”-65°40’39”,9=+0”.1 и т.д.

Проверяем соблюдение четвертого свойства случайных ошибок:

lim[u]/n=-0.8/8=-0.1~0

Вычисляем среднеквадратическую ошибку отдельного измерения (114):

m=±√74,88/7=±√10,69=±3”,27

Вычисляем среднеквадратическую ошибку арифметической середины (115):

М=±√74,88/8*7=±√1,33 =+1”,15

Таким образом измеренный угол в 8 приемах можно записать как:

bср.=65°40’39”,9±1”,15

то-есть среднеарифметическое значение угла 65°40’39”,9 найдено с ошибкой ±1”,15.