Устойчивость оболочек и пластин в пределах упругости

Попытаемся определить критическое продольное сжимающее усилие, приложенное по торцам круговой замкнутой цилиндрической оболочки (см рис.121).

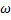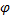Решение. а) Полагаем, что форма оболочки после потери устойчивости остается осесимметричной (рис.). Тогда и не зависят от 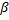и систему (161) можно записать в виде

;

(168)

,

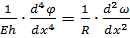где

;

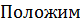
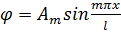(169)

.

Подставим (168) в (167), получим систему алгебраических уравнений относительно 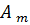и :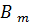

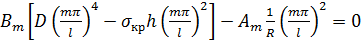; (170)

.

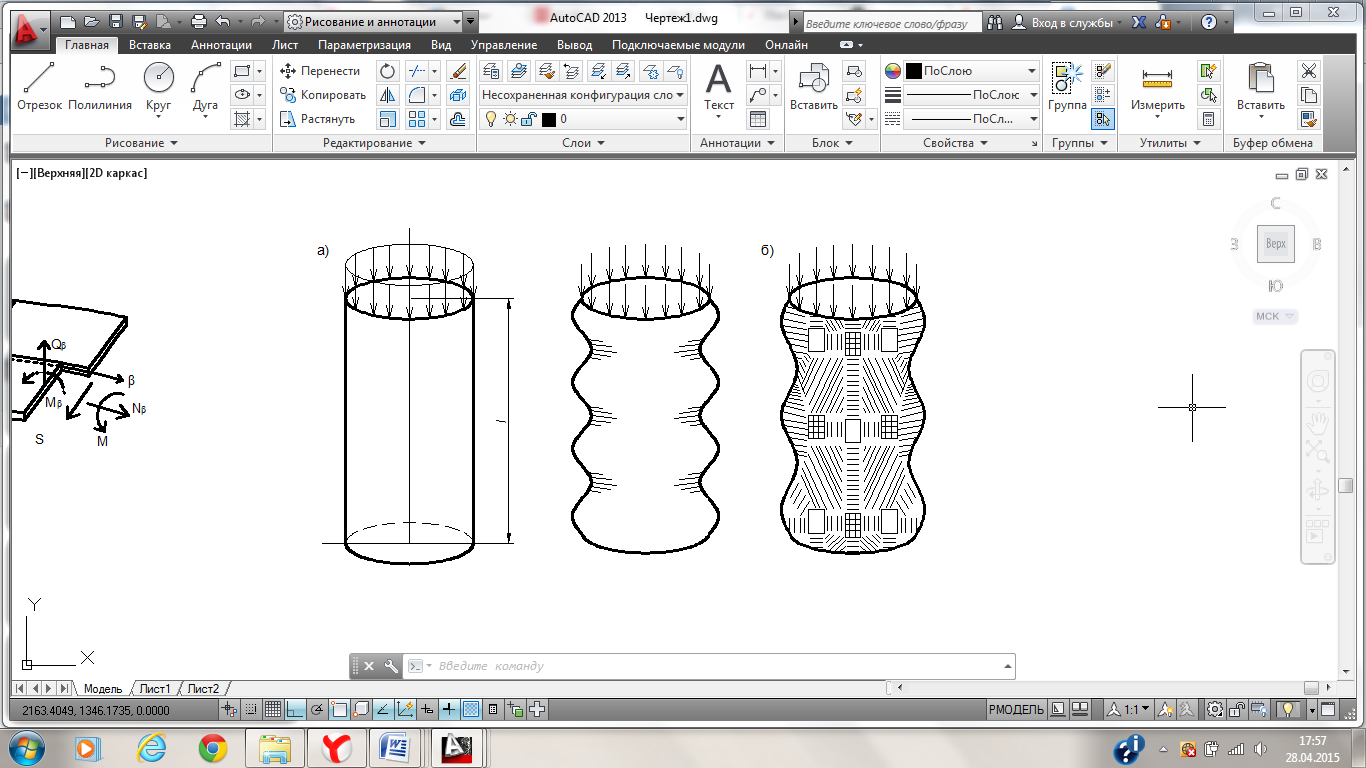
Рис. 121 Определение критического продольного сжимающего усилия, приложенного по торцам круговой замкнутой цилиндрической оболочки

Эта однородная система уравнений будет иметь ненулевое решение только тогда, когда ее детерминант равен нулю:

,

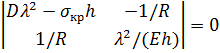где .

Раскрывая определить, получим критическое значение

. (171)

Нужно найти минимальное значение 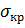, при котором оболочка потеряет устойчивость, для этого должны соблюдаться условия

; .

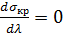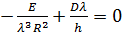Отсюда .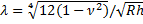

Подставляя это значение в (171), получаем

.

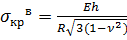Это и будет верхнее критическое напряжение. При 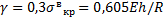. Следовательно, продольная критическая сжимающая сила определяется выражением

.

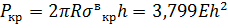б) Полагаем, что оболочка при потере устойчивости не сохраняет своей осесимметричной формы (рис. 121, б) и получает прогиб

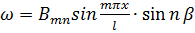, (172)

где m – число полуволн по образующей; n – число полных волн вдоль окружности; x – координата вдоль образующей; 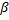- угловая координата.

Примем 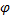изменяющимся по закону

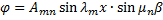, (173)

где 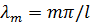; 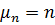. Подставляя (172) и (173) в (170) и полагая 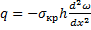, находим

;

.

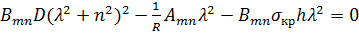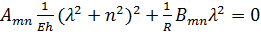Приравнивая детерминант системы нулю, получаем

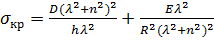. (174)

Наименьшее значение 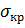получается тогда, когда соблюдается условие

,

тогда

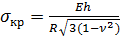. (175)

По итогам расчетов можно сделать вывод, что верхние критические нагрузки при симметричной и несимметричной формах потери устойчивости оболочки совпадают.

Расчет на устойчивость оболочек и пластин можно провести на ПК ЛИРА – САПР

Пластины и оболочки находят достаточно широкое применение в различных областях современной техники. Часто их делают слоистыми. Чередование высокопрочных слоев с легкими маложесткими слоями придает конструкции высокую прочность и жесткость при относительно небольшой массе. Слоистые конструкции и их фрагменты используются в строительстве, машиностроении, авиации и космонавтике. Использование слоев со специальными свойствами позволяет создавать конструкции, которые могут обладать хорошей тепло, электро и звукоизоляцией, радиопрозрачностью, высокой стойкостью к агрессивным средам и др.

Поэтому слоистые конструкции предопределяют повышенные требования к теории расчета их прочности. Теория должна учитывать неоднородность структуры материала по толщине; обладать повышенной точностью в определении напряженного состояния, особенно в краевой зоне и в районах резкого изменения жесткости конструкции; определять с повышенной точностью поперечные напряжения в маложестких слоях. При учете свойств материала на базе упругой модели требуется высокая точность определения всех компонентов напряженного состояния упругой слоистой конструкции.

Наиболее совершенной теорией расчета на прочность слоистых конструкций является теория упругости трехмерного тела. Однако практическое использование трехмерных уравнений теории упругости для расчета слоистых конструкций до настоящего времени представляло значительные трудности, заключающиеся в практическом использовании вычислительных машин с ограниченным объемом памяти.

В расчетах трехмерных инженерных конструкции, в том числе и слоистых конструкций из оболочек, среди других численных методов особую популярность приобрел метод конечных элементов (МКЭ), позволяющий достигать достаточно точных результатов при расчете сплошных систем. Дискретная модель конструкции представляется в виде совокупности отдельных объемных элементов, взаимодействующих между собой в конечном числе узловых точек, и проблема сводится к расчету упругой системы с конечным числом степеней свободы.

Используя программный комплекс «Лира-САПР» 2014 для расчета пластин и оболочек на устойчивость можно получить:

- возможность полной автоматизации процессов формирования матриц жесткости конструкции и решения систем линейных уравнений;

- легкость компоновки гибких алгоритмов расчета, позволяющих путем замены исходных данных изменять граничные условия и характер внешней нагрузки конструкции;

- возможность учета физической и геометрической нелинейности оболочки, влияние температурных воздействии, возникающих в процессе эксплуатации.

-возможность расчета пластин и оболочек на критические нагрузки.

Проблемы, связанные с учетом анизотропии материала и переменности толщин пластин и оболочек, при использовании МКЭ становятся несущественными и решаются довольно просто в процессе задания исходных данных для данного расчета.