Лекция расчет на устойчивость пластин и оболочек

Обеспечение устойчивости равновесиям несущей способности тонкостенных деформируемых систем, состоящих из пластинок и оболочек, является одной из важнейших задач, решаемых при проектировании элементов различных машин и несущих конструкций инженерных сооружений. В прошлом столетии в этих областях происходило бурное развитие технологий, породив широчайший спектр разнообразных задач. Отсюда возникает повышенный интерес к поведению таких конструкций под действием различных внешних нагрузок. Внимание исследователей в первую очередь обращено на проблемы, имеющие непосредственное практическое значение. При расчёте таких систем возникают вопросы об их прочности и устойчивости в работе, т.к. наличие различные условия могут существенно влиять на эти характеристики. Применение метода конечных элементов для моделирования тонкостенных деформируемых систем, позволяет существенно упростить численное исследование и экспериментальную часть таких элементов. Изучение поведения тонкостенных пластин и оболочек, ослабленных отверстиями, важно для понимания механизмов взаимодействия отверстий с системами, разработки математических моделей, внедрения новых технологий.

Аналитически задача исследования устойчивости упругих тел сводится к решению граничных задач на собственные значения, причём потери устойчивости соответствует наименьшее собственное значение, зависящее от набора параметров. В связи с наличием отверстий рассматриваемые области оказываются многосвязными. Исследование поведения собственных чисел для таких областей представляет теоретический интерес.

Рассмотрим составляющие напряженного и деформированного состояния оболочки с помощью известного из теории упругости алгоритма.

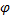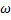Составляющие напряженного и деформационного состояния оболочки выражаются через и следующим образом:

; ; ;

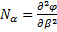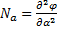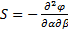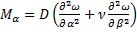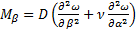; ; (161)

;

; .

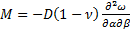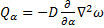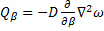Все расчетные усилия показаны на рис. 120

; ; ;

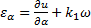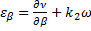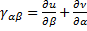(162)

; ; .

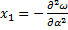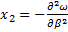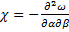Предполагая, что оболочка пологая, по крайней мере, в пределах одной вмятины, можно записать и уравнение для исследования устойчивости при больших прогибах:

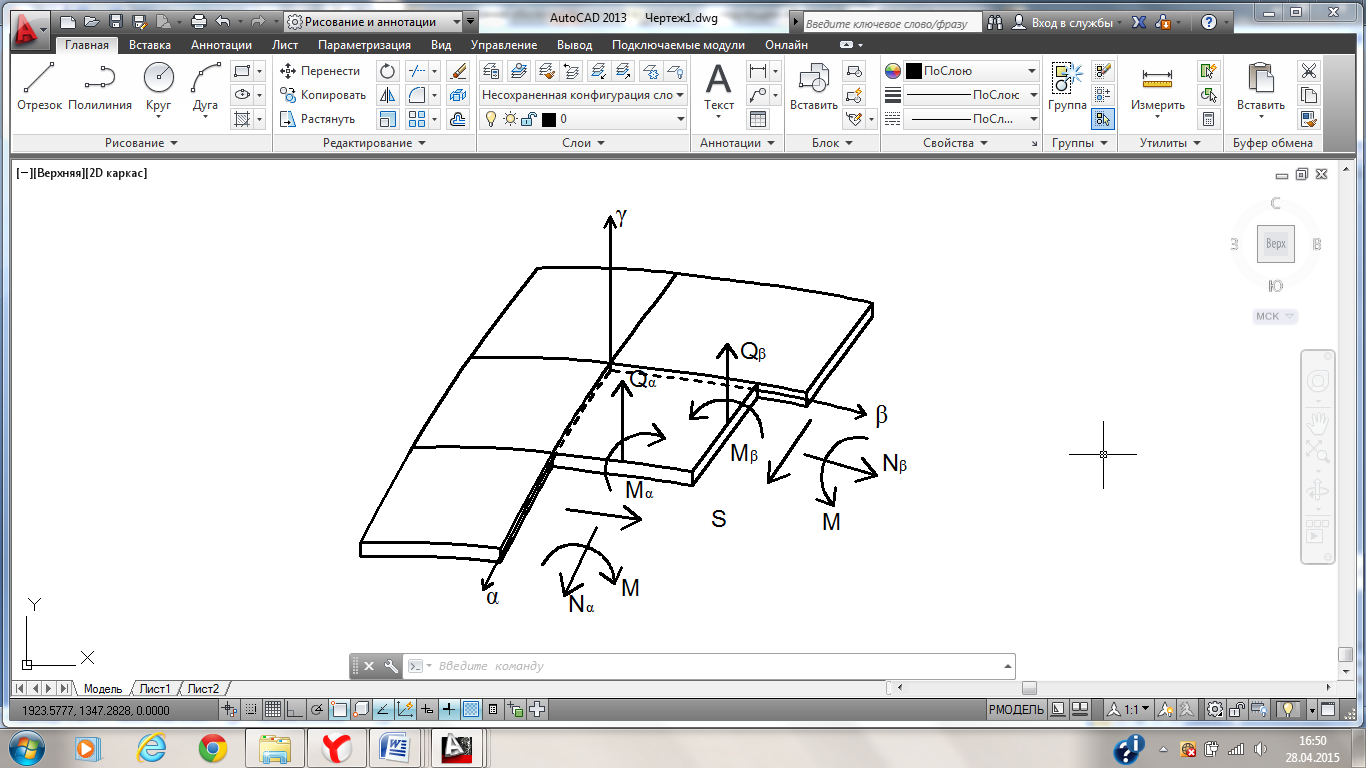
Рис. 120 Расчетная схема пологой оболочки с приложенными усилиями

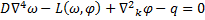; (163)

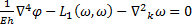; (164)

;

.

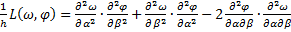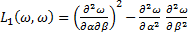В уравнении (163) нелинейные члены появляются в выражениях для деформаций в срединной поверхности оболочкой:

;

;

.

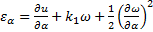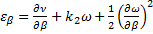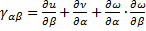При исследовании потери устойчивости оболочки энергетическим методом используют выражения потенциальной энергии деформаций

,

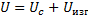Где 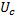- энергия деформации срединной поверхности оболочки; 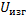- энергия изгиба. Эти составляющие определяются по формулам

;

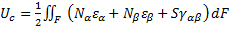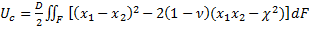. (165)

Интегрирование следует распределить на всю поверхность оболочки. Работа внешних сил на перемещениях в момент потери устойчивости записывается для каждого конкретного случая. Критические усилия определяются из условия равенства энергии деформации и работы внешних сил, действующих на оболочку.

Задачу об устойчивости пластин удобно рассматривать как частный случай задачи об устройстве оболочек. Положив в уравнениях (163) кривизны k₁ и k₂ равными нулю, получим уравнения для определения критических напряжений в пластинах. Решая задачу для малых прогибов, считают, что при выпучивании напряжения в срединной плоскости пластины малы по сравнению с напряжением изгиба. Пренебрегая напряжениями плоского напряженного состояния, получают одно уравнение для исследования устойчивости пластин

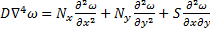, (166)

где 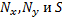- внутренние усилия в пластине, вызванные нагрузкой, приложенной по контору в плоскости пластины.

Потенциальная энергия деформации для пластины определяется выражением (165) при условии, что кривизны k₁ и k₂ равны нулю.

При исследовании поведения пластины после потери устойчивости (в закритической области) приходится учитывать проблемы и использовать более общую теорию гибких пластин. Уравнение для этой задачи можно получить из (166), приравнивая k₁ и k₂ к нулю:

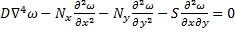; (167)

.

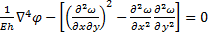Функция напряжения 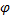и прогиб 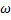связаны с усилиями и моментами формулами (161).