Общие принципы и этапы построения

2.1. Определение и назначение моделирования.

Классификация математических моделей

Модельимоделирование - универсальные понятия, атрибуты одного из наиболее мощных методов познания в любой профессиональной области, познания системы, процесса, явления.

Целью моделирования являются получение, обработка, представление и использование информации об объектах, которые взаимодействуют между собой и внешней средой; а модель здесь выступает как средство познания свойств и закономерности поведения объекта.

По уровню, «глубине» моделированиямодели бывают:

– эмпирические - на основе эмпирических фактов, зависимостей;

– теоретические - на основе математических описаний;

– смешанные, полуэмпирические - на основе эмпирических зависимостей и математических описаний.

Проблема моделирования состоит из трех задач [6]:

– построение модели(эта задача менее формализуема и конструктивна, в том смысле, что нет алгоритма для построения моделей);

– исследование модели(эта задача более формализуема, имеются методы исследования различных классов моделей);

– использование модели (конструктивная и конкретизируемая задача).

Построение модели – системная задача, требующая анализа и синтеза исходных данных, гипотез, теорий, знаний специалистов. Системный подход позволяет не только построить модель реальной системы, но и использовать эту модельдля оценки (например, эффективности управления, функционирования) системы.

Слово «модель» происходит от латинского modus (копия, образ, очертание). Моделирование – это замещение некоторого объекта А другим объектом Б. Замещаемый объект А называется оригиналом или объектом моделирования, а замещающий Б – моделью. Другими словами, модель – это объект-заменитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала.

Под математической модельюбудем понимать любой оператор L, позволяющий по соответствующим значениям входных парамет­ров X установить выходные значения параметров Y объекта модели­рования:

L: Х→ Y, XÎ Ω_X, YÎ Ω_Y, (2.1)

где Ω_X и Ω_Y – множества допустимых значений входных и выход­ных параметров для моделируемого объекта. В зависимости от при­роды моделируемого объекта элементами множеств Ω_X и Ω_Y могут являться любые математические объекты (числа, векторы, тензо­ры, функции, множества и т.п.).

Схема отображения системы S в модель М с множеством входов Ω_X и выходов Ω_Y изображена на рис. 2.1.

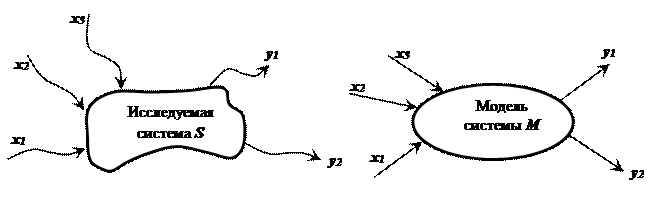
Рис. 2.1. Схема отображения системы S в модель М

Понятие оператора в приведенном определении может тракто­ваться достаточно широко. Это может быть как некоторая функция, связывающая входные и выходные значения, так и отображение, представляющее символическую запись системы алгебраических, дифференциальных, интегродифференциальных или интегральных уравнений. Наконец, это может быть некоторый алгоритм, сово­купность правил или таблиц, обеспечивающих нахождение (или установление) выходных параметров по заданным исходным зна­чениям.

Определение математической модели через понятие оператора является более конструктивным с точки зрения построения классификации таких моделей, поскольку включает в себя все много­образие имеющихся в настоящее время математических моделей.

Бурное развитие методов математического моделирования и многообразие областей их использования привело к появлению ог­ромного количества моделей самого разного типа. В связи с этим возникает необходимость в определенном упорядочивании, клас­сификации существующих и появляющихся математических моде­лей. Учитывая большое число возможных классификационных признаков и субъективность их выбора, появление все новых клас­сов моделей, следует отметить условность и незавершенность рас­сматриваемой ниже классификации [7].

Представляется возможным подразделить математические мо­дели на различные классы в зависимости от:

– сложности объекта моделирования;

– оператора модели (подмодели);

– входных и выходных параметров;

– способа исследования модели;

– цели моделирования.

Рассмотрим классификацию математических моделей в зависимости от сложности объекта моделирования [7].

Вкачестве объекта моделирования может выступать как неко­торое материальное тело или конструкция, так и природный, тех­нологический или социальный процесс либо явление. Все объекты моделирования можно разделить на две группы: простые и объек­ты-системы (рис. 2.2).

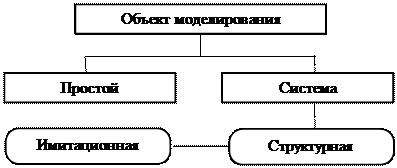
Рис. 2.2. Классификация объектов моделирования

В первом случае при моделировании не рас­сматривается внутреннее строение объекта, не выделяются состав­ляющие его элементы или подпроцессы. В качестве примера подоб­ного объекта можно привести материальную точку в классической механике.

Модели объектов-систем, учитывающие свойства и поведение отдельных элементов, а также взаимосвязи между ними, называ­ются структурными.Среди структурных динамических систем выделяют в отдель­ный подкласс имитационныесистемы, состоящие из конечного числа элементов, каждый из которых имеет конечное число состо­яний. Число связей между элементами также предполагается конеч­ным. Моделирование взаимодействий элементов внутри системы осуществляется с помощью некоторого алгоритма, реализуемого обычно с использованием ЭВМ.

Рассмотрим классификацию математических моделей в зависимости от оператора модели [7].

Выше отмечалось, что любая математическая модель может рас­сматриваться как некоторый оператор L, который является алго­ритмом или определяется совокупностью уравнений - алгебраи­ческих, обыкновенных дифференциальных уравнений (ОДУ), си­стем ОДУ (СОДУ), дифференциальных уравнений в частных производных (ДУЧП), интегродифференциальных уравнений (ИДУ) и др. (рис. 2.3).

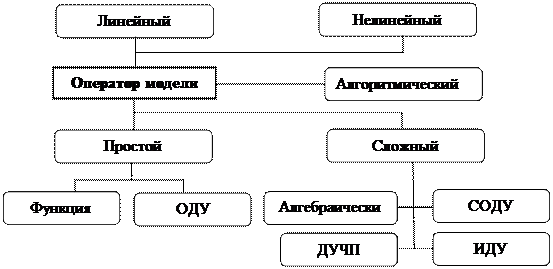Рис. 2.3. Классификация в зависимости от вида оператора модели

В зависимости от вида оператора математические модели мож­но разделить на простыеи сложные.

В случае, когда оператор модели является алгебраическим вы­ражением, отражающим функциональную зависимость выходных параметров Y от входных X, модель будем называть простой.

Простые модели чаще всего являются результатом обобщения и анализа экспериментальных данных, полученных в результате на­блюдений за исследуемым объектом или явлением. Модель, включающая системы дифференциальных и интеграль­ных соотношений, уже не может быть отнесена к простым, так как для своего исследования требует применения довольно сложных ма­тематических методов. Однако в двух случаях она может быть све­дена к простым:

1) если полученная для подобной модели система математических соотношений может быть разрешена аналитически;

2) если результаты вычислительных экспериментов со сложной
моделью аппроксимированы некоторой алгебраической зависимо­стью. В настоящее время известно достаточно большое число подходов и методов аппроксимации (например, метод наименьших квадратов или метод планирования экспериментов).

Далее рассмотрим классификацию математических моделей в зависимости от параметров модели (рис. 2.4).

Вобщем случае параметры, описывающие состояние и поведе­ние объекта моделирования, разбиваются на ряд непересекающих­ся подмножеств:

- совокупность входных (управляемых) воздействий на объект Ω_X ;

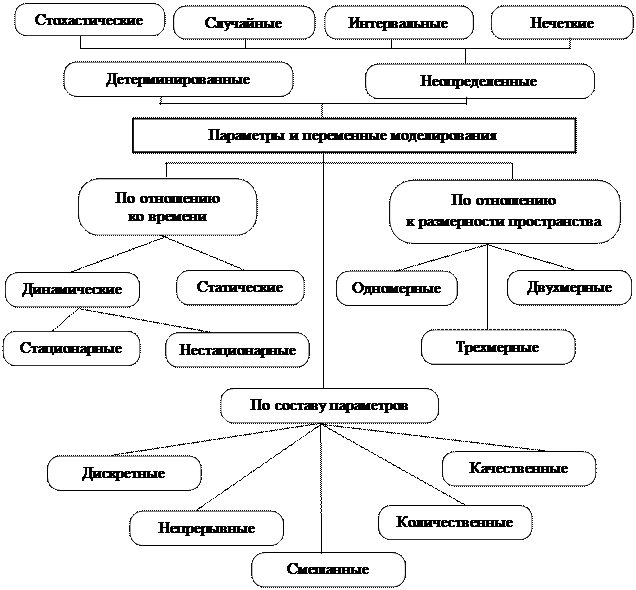
Рис.2.4. Классификация математических моделей в зависимости от параметров

- совокупность воздействий внешней среды (неуправляемых) Ω_E;

- совокупность внутренних (собственных) параметров объекта Ω_Z;

- совокупность выходных характеристик Ω_Y.

При построении модели возможны следующие варианты описания неопределенности параметров [7]:

1) детерминированное - значения всех параметров модели определяются детерминированными величинами (т.е. каждому пара­метру соответствует конкретное целое, вещественное или комплек­сное число либо соответствующая функция). Данный способ соот­ветствует полной определенности параметров;

2) стохастическое- значения всех или отдельных параметров модели определяются случайными величинами, заданными плот­ностями вероятности. В литературе наиболее полно исследованы случаи нормального (гауссова) и показательного распределения случайных величин;

3) случайное- значения всех или отдельных параметров моде­ли устанавливаются случайными величинами, заданными оценками плотностей вероятности, полученными в результате обработки ограниченной экспериментальной выборки данных параметров. Эта форма описания тесно связана с предыдущей. Однако в рассматри­ваемом случае получаемые результаты моделирования будут существенным образом зависеть от точности оценок моментов и плотностей вероятности случайных параметров, от постулируемых законов распределения и объема выборок;

4) интервальное- значения всех или отдельных параметров мо­дели описываются интервальными величинами, заданными интервалом, образованным минимальным и максимально возможными значениями параметра;

5) нечеткое- значения всех или отдельных параметров модели
описываются функциями принадлежности соответствующему нечеткому множеству. Такая форма используется, когда информация о параметрах модели задается экспертом на естественном языке, а следовательно, в «нечетких» (с позиции математики) терминах типа «много больше пяти», «около нуля».

Разделение моделей на одномерные, двухмерныеи трехмерныеприменимо для таких моделей, в число параметров которых входят координаты пространства, и связано с особенностями реализации этих моделей, равно как и с резким увеличением их сложности при возрастании размерности (с «проклятием размерности» по образно­му выражению Р. Беллмана). Как правило, увеличение размернос­ти модели приводит к росту числа используемых математических соотношений. Особенно сложны в реализации трехмерные модели, требующие высокопроизводительной вычислительной техники с большим объемом оперативной и дисковой памяти. При разработке модели стараются (если это возможно) понизить размерность. Необоснованное пониже­ние размерности модели может существенно исказить результаты моделирования.

Из всей совокупности параметров при разработке различных моделей отдельно следует рассмотреть учет времени. Как и коор­динаты, время относится к независимым переменным, от которых могут зависеть остальные параметры модели. В различных ситуа­циях объект исследования может по разному испытывать влияние времени. Обычно чем меньше масштаб объекта, тем существеннее зависимость его параметров от времени.

Классификация математических моделей в зависимости от целей моделирования представлена на рис. 2.5.

Рис. 2.5. Классификация в зависимости от целей моделирования

Целью дескриптивных моделей(от лат. descriptio - описание) яв­ляется установление законов изменения параметров модели. В ка­честве примера такой модели можно привести модель движения ма­териальной точки под действием приложенных сил, использующая второй закон Ньютона. Задавая положение и скорость точки в на­чальный момент времени (входные параметры), массу (собствен­ный параметр) и закон изменения прикладываемых сил (внешние воздействия), можно определить скорость и координаты материаль­ной точки в любой момент времени (выходные параметры). Полу­ченная модель описывает зависимость выходных параметров от входных. Поэтому дескриптивные модели являются реализацией описательных и объяснительных содержательных моделей на фор­мальном уровне моделирования.

Оптимизационные моделипредназначены для определения оп­тимальных (наилучших) с точки зрения некоторого критерия па­раметров моделируемого объекта или же для поиска оптимального (наилучшего) режима управления некоторым процессом. Часть параметров модели относят к параметрам управления, изменяя которые можно получать различные варианты наборов значений выходных параметров. Как правило, данные модели строятся с использованием одной или нескольких дескриптивных моделей и включают некоторый критерий, позволяющий сравнивать различ­ные варианты наборов значений выходных параметров между со­бой с целью выбора наилучшего. На область значений входных параметров могут быть наложены ограничения в виде равенств и неравенств, связанные с особенностями рассматриваемого объекта или процесса. Целью оптимизационных моделей является поиск таких допустимых параметров управления, при которых критерий выбора достигает своего «наилучшего значения».

Управленческие моделиприменяются для принятия эффектив­ных управленческих решений в различных областях целенаправлен­ной деятельности человека. В отличие от оптимизационных моделей, где критерий выбора считается определенным и искомое решение ус­танавливается из условий его экстремальности, в управленческих моделях необходимо введение специфических критериев оптималь­ности, которые позволяют сравнивать альтернативы при различных неопределенностях задачи.

Классификация математических моделей в зависимости от методов реализации приведена на рис. 2.6.

Метод реализации модели относят к аналитическим, если он по­зволяет получить выходные параметры в виде аналитических выражений, т.е. выражений, в которых используется не более чем счет­ная совокупность арифметических операций и переходов к пределу. Очень часто аналитическое решение для модели представляют в элементарных или специальных функциях: показательных, лога­рифмических, тригонометрических, гиперболических и т.п. Для по­лучения значений этих функций при конкретных значениях вход­ных параметров используют их разложение в ряды (например, Тей­лора). Аналитические методы реализации модели являются более цен­ными в том плане, что позволяют с меньшими

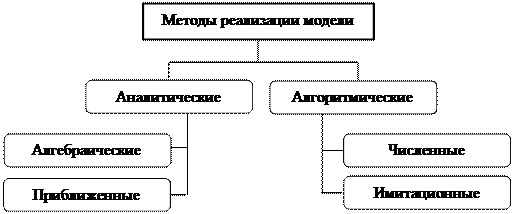Рис. 2.6. Классификация в зависимости от методов реализации

вычислительными затратами изучить свойства объекта моделирования, применяя тра­диционные хорошо развитые математические методы анализа ана­литических функций. Существенно, что применение аналитичес­ких методов возможно без использования ЭВМ (за исключением случаев, когда аналитическое решение определяется в рядах и для его доведения до числа требуются трудоемкие вычисления с при­менением ЭВМ). Кроме того, знание аналитического выражения для искомых параметров позволяет исследовать фундаментальные свойства объекта, его качественное поведение, строить новые ги­потезы о его внутренней структуре. Следует отметить, что возмож­ности аналитических методов существенно зависят от уровня раз­вития соответствующих разделов математики.

В настоящее время мощный всплеск интереса к аналитическим методам при реализации моделей связан с появлением пакетов ма­тематических вычислений (MATHCAD^®, MATLAB^®, MATHEMATICA^® и др.). Спектр решаемых данными пакетами задач очень велик и постоянно расширяется (элементар­ная математика, символьные операции с полиномами, производны­ми и интегралами, с векторами и матрицами, задачи теории поля и векторного анализа, метод конечных элементов и т.п.). Примене­ние подобных программных средств не только упрощает процеду­ру получения аналитического решения, но и облегчает последую­щий анализ полученного решения с применением различного рода визуализаторов. Возможности математического пакета MATHCAD^® и примеры его применения будут рассмотрены далее и на практических занятиях.

При численном подходесовокупность математических соотно­шений модели заменяется конечномерным аналогом. Это чаще всего достигается дискретизацией исходных соотношений, т.е. переходом от функций непрерывного аргумента к функциям дискрет­ного аргумента. После дискретизации исходной задачи выполня­ется построение вычислительного алгоритма, т.е. последовательно­сти арифметических и логических действий, выполняемых на ЭВМ и позволяющих за конечное число шагов получить решение диск­ретной задачи. Найденное решение дискретной задачи принимает­ся за приближенное решение исходной математической задачи.

Степень приближения определяемых с помощью численного метода искомых параметров модели зависит как от погрешностей са­мого метода, связанных с заменой исходной модели ее дискретным аналогом, так и от ошибок округления,возникающих при выполне­нии любых расчетов на ЭВМ в связи с конечной точностью пред­ставления чисел в ее памяти. Основным требованием к вычисли­тельному алгоритму является необходимость получения решения исходной задачи с заданной точностьюза конечное число шагов. Возможности пакетовANSYS^®, LS-DYNA3D^® для решения задач ОМД методом конечных элементов и примеры его применения будут рассмотрены далее и на практических занятиях.

Если при численном подходе дискретизации подвергалась по­лученная система математических соотношений, то при имитаци­онном подходена отдельные элементы разбивается сам объект ис­следования. В этом случае система математических соотноше­ний для объекта-системы в целом не записывается, а заменяется некоторым алгоритмом, моделирующим ее поведение и учитыва­ющим взаимодействие друг с другом моделей отдельных элемен­тов системы. Модели отдельных элементов могут быть как анали­тическими, так и алгебраическими.

Алгоритмические модели, использующие как численный, так и имитационный подход, не позволяют получить решения задач в аналитической форме, что затрудняет и усложняет процесс анали­за результатов моделирования. Так как применение моделей дан­ного типа возможно лишь при наличии вычислительной техники, то их эффективность зависит от мощности и быстродействия ЭВМ. Несомненным достоинством алгоритмических моделей является отсутствие принципиальных ограничений на сложность модели, что позволяет применять их для исследования систем произвольной сложности.

Использование математической модели, построенной алгорит­мическими методами, аналогично проведению экспериментов с реальным объектом, только вместо реального эксперимента с объек­том проводится вычислительный экспериментс его моделью. Зада­ваясь конкретным набором значений исходных параметров модели, в результате вычислительного эксперимента находим конкретный набор приближенных значений искомых параметров. Для исследо­вания поведения объекта при новом наборе исходных данных необ­ходимо проведение нового вычислительного эксперимента.

В обработке металлов давлением математические модели классифицируются по следующим признакам [7]:

– по назначению;

– по происхождению;

– по состоянию системы оборудование–обрабатываемая заготовка;

– по точности.

По назначению математические модели ОМД подразделяются на описательные и оптимизирующие. Описательные модели предназначены только для описания процесса, т.е. только для прогнозирования его параметров. оптимизирующие модели, кроме описания процесса содержат обязательно, некоторую целевую функцию.

По происхождению, т.е. по источнику получения использованных исходных предположений, математические модели процессов ОМД делятся на теоретические и экспериментальные. Теоретические модели создаются на основе наиболее общих современных научных знаний о процессе пластической деформации металлов и сплавов с использованием минимального объема экспериментальных данных. Базой для создания таких моделей служит современная теория механики сплошных сред и обработки металлов давлением. Экспериментальные модели создаются на основе статистического анализа наблюдений за ходом процесса и установления корреляционных связей между его параметрами.

По состоянию системы оборудование–обрабатываемая заготовка модели подразделяются на динамические и статические. Динамические модели предназначены для описания процесса ОМД в его развитии. Поэтому во всех динамических моделях входит время протекания процесса. Наличие временной характеристики в динамических моделях позволяет учитывать влияние любой нестационарности (кинематической, температурной, силовой, геометрической и т.п.) при прогнозировании параметров процесса ОМД и поведения системы оборудование–обрабатываемая заготовка. Динамические модели обеспечивают наиболее полное и всесторонне описание процесса ОМД как в нестационарных, так и стационарных условиях.

Моделирование – метод системного анализа. Но часто в системном анализе при модельном подходе исследования может совершаться одна методическая ошибка, а именно, - построение корректных и адекватных моделей (подмоделей) подсистем системы и их логически корректная увязка не дает гарантий корректности построенной таким способом модели всей системы. Модель, построенная без учета связей системы со средой и ее поведения по отношению к этой среде, может часто лишь служить еще одним подтверждением теоремы Геделя (о неполноте формальных систем), а точнее, ее следствия, утверждающего, что в сложной изолированной системе могут существовать истины и выводы, корректные в этой системе и некорректные вне ее.

Моделирование(в значении "метод", "модельный эксперимент") рассматривается как особая форма эксперимента, эксперимента не над самим оригиналом (это называется простым или обычным экспериментом), а над копией (заместителем) оригинала. Здесь важен изоморфизм систем (оригинальной и модельной) – изоморфизм, как самой копии, так и знаний, с помощью которых она была предложена.

Модели и моделирование применяются по основным направлениям:

– обучение (как моделям, моделированию, так и самих моделей);

– познание и разработка теории исследуемых систем (с помощью каких-либо моделей, моделирования, результатов моделирования);

– прогнозирование (выходных данных, ситуаций, состояний системы);

– управление (системой в целом, отдельными подсистемами системы), выработка управленческих решений и стратегий;

– автоматизация (системы или отдельных подсистем системы).

2.2. Системные принципы построения математических моделей

Математические модели в количественной форме, с помощью логико-математических конструкций, описывают основные свойства объекта, процесса или системы, его параметры, внутренние и внешние связи.

Для построения математической модели необходимо:

– тщательно проанализировать реальный объект или процесс;

– выделить его наиболее существенные черты и свойства;

– определить переменные, т.е. параметры, значения которых влияют на основные черты и свойства объекта;

– описать зависимость основных свойств объекта, процесса или системы от значения переменных с помощью логико-математических соотношений (уравнения, равенства, неравенства, логико-математические конструкций);

– выделить внутренние связи объекта, процесса или системы с помощью ограничений, уравнений, равенств, неравенств, логико-математических конструкций;

– определить внешние связи и описать их с помощью ограничений, уравнений, равенств, неравенств, логико-математических конструкций.

Математическое моделирование, кроме исследования объекта, процесса или системы и составления их математического описания, также включает:

- построение алгоритма, моделирующего поведение объекта, процесса или системы;

- проверка адекватности модели и объекта, процесса или системы на основе вычислительного и натурного эксперимента;

- корректировка модели;

- использование модели.

Математическое описание исследуемых процессов и систем зависит от:

- природы реального процесса или системы и составляется на основе законов физики, химии, механики, термодинамики, гидродинамики, электротехники, теории пластичности, теории упругости и т.д.

- требуемой достоверности и точности изучения и исследования реальных процессов и систем.

На этапе выбора математической модели устанавливаются: линейность и нелинейность объекта, процесса или системы, динамичность или статичность, стационарность или нестационарность, а также степень детерминированности исследуемого объекта или процесса. При математическом моделировании сознательно отвлекаются от конкретной физической природы объектов, процессов или систем и, в основном, сосредотачиваются на изучении количественных зависимостей между величинами, описывающими эти процессы.

Математическая модель никогда не бывает полностью тождественна рассматриваемому объекту, процессу или системе. Основанная на упрощении, идеализации она является приближенным описанием объекта. Поэтому результаты, полученные при анализе модели, носят приближенный характер. Их точность определяется степенью адекватности (соответствия) модели и объекта.

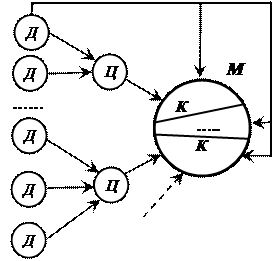
Построение (синтез) математической модели может основываться на классическом и системном подходах [10] (рис. 2.7). Процесс синтеза модели М на основе классического подхода (индуктивного) подхода представлен на рис. 2.7а. Реальный объект, подлежащий моделированию, разбивается на отдельные подсистемы, т.е. выбираются исходные данные Д для моделирования и ставятся цели Ц, отображающие отдельные стороны процесса моделирования. По отдельной совокупности исходных данных Д ставится цель моделирования отдельной стороны функционирования системы, на базе этой цели формируется некоторая компонента К будущей модели. Совокупность компонент объединяется в модель.

Таким образом, разработка модели М на базе классического подхода означает суммирование отдельных компонент в единую модель, причем каждая из компонент решает свои собственные задачи и изолирована от других частей модели.

Классический подход может быть использован для реализации сравнительно простых моделей, в которых возможно разделение и взаимно независимое рассмотрение отдельных сторон функционирования реального объекта. Для модели сложного объекта такая разобщенность решаемых задач недопустима, так как приводит к значительным затратам ресурсов при реализации модели на базе конкретных программно-технических средств. Можно отметить две отличительные стороны классического подхода: наблюдается движение от частного к общему, создаваемая модель (система) образуется путем суммирования отдельных её компонент и не учитывает возникновение нового системного эффекта.

а)

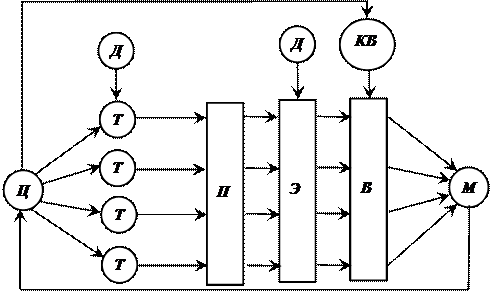б)

Рис. 2.7. Процесс синтеза модели на основе классического а) и системного б) подходов

Процесс синтеза модели М на основе системного подхода представлен на рис. 2.7б. На основе исходных данных Д, которые известны из анализа внешней надсистемы (среды), тех ограничений, которые накладываются на систему сверху либо исходя из возможностей её реализации, и на основе цели функционирования формулируются исходные требования Т к модели системы S. На базе этих требований формулируются ориентировочно некоторые подсистемы П, элементы Э и осуществляется наиболее сложный этап синтеза – выбор В составляющих системы, для чего используются специальные критерии выбора КВ.