Закон Ома для неоднородного участка цепи

ЗО в дифференциальной форме имеет вид: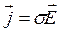с другой стороны плотность тока определяется скоростью направленного движения носителей то­ка, и, если они имеют одинаковые знаки, 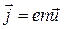. Сравнивая эти две фор­мулы, можно заключить, что скорость упорядоченного движения 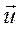носителей тока пропорциональна напряженности электрического поля. Отметим, что такая связь может наблюдаться только в том случае, если кроме силы вызывающей движение, на тело действует сила сопротивления среды. Эта сила обусловлена взаимодействием носителей тока с веществом проводника и приводит к сущест­вованию сопротивления проводников.

Очевидно, что если на участке цепи, кроме электростатической силы, дей­ствуют сторонние силы, то средняя скорость упорядоченного движения будет пропорциональна результирующей силе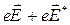, а значит

(17.18)

(17.19)

(17.20)

(17.21)

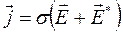
Формула (17.18) выражает закон Ома для неоднородного участка цепи в дифферен­циальной форме.

Получим выражение для ЗО в интегральной форме для неоднородного участ­ка цепи. Рассмотрим внутри неоднородного участка цепи линию, такую, что в любом сечении, перпендикулярном к ней величины 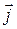, , 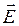, 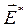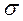имеют одинако­вые значения, а направлены 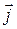, , 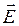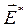по касательной к линии. Такую линию называют контуром тока. Выберем направление движения по контуру например от 1 к 2. Спроектируем (17.18) на некоторый элементов 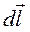контура:

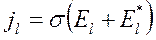
Проекции векторов будут равны их модулям, взятым со знаком, зависящим от направления соответствующего вектора. Сила тока в каж­дом сечений контура должна быть одинаковой, т. к. в противном случае в сечении будет накапливаться заряд. Выразив плотность тока через его силу, получим из (17.19):

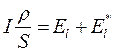
Умножим (17.20) на 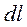и проинтегрируем вдоль участка контура:

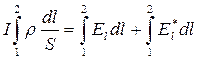
После интегрирования получаем:

(17.22)

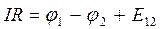
В (17.22) сила тока и 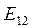являются алгебраическими величинами: если ток направ­лен вдоль направлений движений по контуру, то он положителен; ЭДС положи­тельна в том случае, если она способствует движению носителей тока в выбранном направлении.

Разделив (17.22) на R, получим выражение для ЗО в интегральной форме для неоднородного участка цепи:

(17.23)

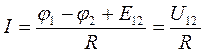
Соответственно для замкнутой цепи

(17.24)

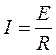
Правила Кирхгофа

Изучить самостоятельно

Мощность тока.

Если к некоторому участку цепи приложено напряжение U и по нему протекает ток I, то за время t через поперечное сечение проводника бу­дет перенесен заряд 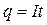. Электростатические и сторонние силы совер­шат над зарядом работу

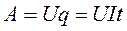(23)

Следовательно, мощность, развиваемая током на данном участке цепи определяется интегральным выражением.

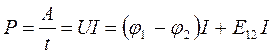(24)

Эта мощность может расходоваться на совершение участком цепи работы при его перемещении, на протекание химических реакций и на нагревание участка цепи.

Удельной мощностью тока 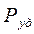называют отношение мощности, развиваемой током в объеме проводника, к объему 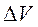проводника:

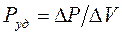(25)

Выделяемая в проводнике мощность определяется работой, совершаемой над но­сителями тока. На каждый из носителей действует сила 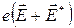, которая развивает мощность

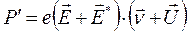(26)