Определение сопротивления и индуктивности коаксиальной цепи

При определении сопротивления и индуктивности в коаксиальной цепи используется тот же подход, что был приведен и для симметричного кабеля, основанный на использовании дифференциальных уравнений электродинамики (уравнений Максвелла и волновых уравнений) и теоремы Умова-Пойтинга. Для внутреннего проводника коаксиальной пары полностью справедлива методика расчета одиночного проводника симметричной цепи (низкочастотный режим передачи).

Поскольку электромагнитное поле внешнего проводника никакого действия на внутренний проводник не оказывает, то полное сопротивление внут­реннего проводника определяется:

,

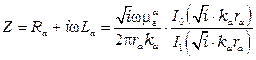где k_a – коэффициенты вихревых токов внутреннего проводника 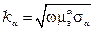; 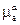– абсолютная магнитная проницаемость внутреннего проводника.

В этом случае сопротивление внутреннего проводника определится по формуле (24)

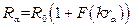
а индуктивность по формуле (25)

.

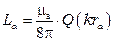При больших 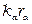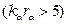соответст­вующем высокочастотной области передачи отношение 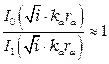. Тогда

.

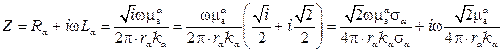Откуда

.

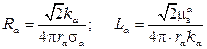Для нахождения параметров внешнего проводника уравнения Максвелла и волновое уравнение будет точно таким же, что и для внутреннего. Отличие будет состоять в граничных условиях. Поэтому второй член уравнения (16)

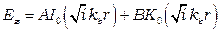
будет не нулевым.

Для оп­ределения полного сопротивления внешнего проводника снова вос­пользуемся теоремой Умова–Пойтинга, согласно которой

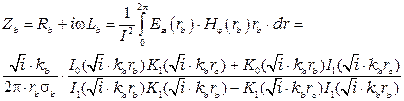
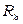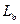Выделив действительную и мнимую части из полученного выражения, можно рассчитывать и при любой частоте тока.

Для практических расчетов при 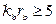(это выполняется для мед­ных проводников при частоте 60кГц и выше) сопротивление 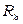и ин­дуктивность 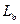могут быть определены по формулам

,

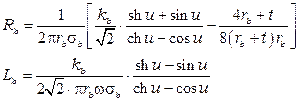где 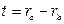– толщина внешнего проводника; .

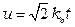Если вели­чина 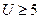, то значение 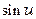и 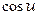в сравнении с 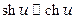можно пренебречь. Тогда

.

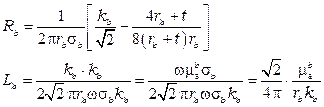Для частот свыше 60 кГц в формуле для определения 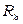вторым слагаемым в скобке по отношению к первому можно пре­небречь и тогда

.

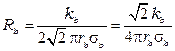Таким образом, для практических расчетов при частотах свыше 60кГц полное сопротивление внутреннего и внешнего проводников коаксиальной цепи можно рассчитывать по приближенной формуле

,

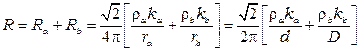где 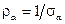и 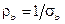– удельные электрические сопротивления металлов, из которого выполнены внутренний и внешний проводники, соответственно, Ом×м; 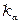, 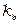– коэффициенты вихревых токов внутреннего и внешнего проводников, соответственно; 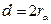, 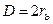– диаметр внутреннего проводника и внутренний диаметр внешнего проводника (диаметр по изоляции).

Полная индуктивность коаксиальной цепи определяется по формуле

,

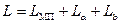где 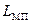– межпроводниковая индуктивность.

Межпроводниковая индуктивность коаксиальной цепи определяется по формуле

,

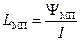где 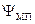– межпроводниковое потокосцепление.

,

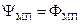где 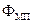– межпроводниковый магнитный поток, обусловленный током от внутреннего проводника.

.

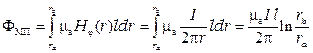Тогда внешняя индуктивность коаксиальной цепи на единицу длины определится по формуле

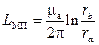. (30)

Таким образом, для частот свыше 60 кГц полная индуктивность коаксиальной цепи определится по формуле

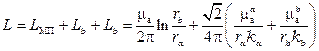
или

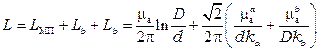
В области высоких частот 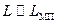, т.к. 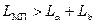, тогда индуктивность коаксиальной пары может быть определена по формуле

.

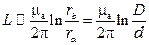Зависимость сопротивления и индуктивности коаксиальной пары от частоты имеет тот же характер, что и для симметричных кабелей.

3.5.2 Определение емкости и проводимости изоляции коаксиальной цепи

При определении емкости коаксиального кабеля учитывают, что он аналогичен цилиндрическому конденсатору и его электриче­ское поле создается между двумя цилиндрическими поверхностями с общей осью. Напряженность электрического поля внутри кабеля на равнопотенциальной поверхности радиуса r определится как

.

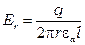Напряжение между внутренним и внешним проводниками определится

.

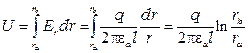Тогда емкость коаксиального кабеля

,

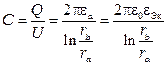где 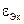– эквивалентное значение относительной диэлектрической проницаемости.

Проводимость изоляции определяется по вышеприведенной формуле, полученной для симметричного кабеля

,

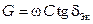где 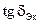– эквивалентное значение тангенса угла диэлектрических потерь.

Ориентировочные значения эквивалентных значений относительной диэлектрической проницаемости и тангенса угла диэлектрических потерь воздушно-комбинированной изоляции коаксиальных кабелей можно вычислить по формулам

,

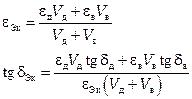где 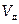, 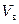– объемы твердого диэлектрика и воздуха на единице длины коаксиальной пары; 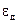, 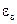– относительные диэлектрические проницаемости твердого диэлектрика и воздуха на единице длины коаксиальной пары.

Необходимо отметить, что приведенные формулы для определения эквивалентных значений относительной диэлектрической проницаемости и тангенса угла диэлектрических потерь воздушно-комбинированной изоляции коаксиальных кабелей не учитывают влияние взаимного расположения на результирующие свойства 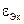и .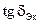

Зависимость емкости и проводимости коаксиальной пары от частоты имеет тот же характер, что и для симметричных кабелей.

3.5.4 Особенности расчета вторичных параметров коаксиаль­ного кабеля

Коаксиальные кабели практически используются в спектре от 60 кГц и выше, поэтому вторичные параметры можно рассчитывать по следующим формулам

, , ,

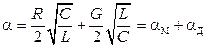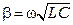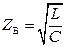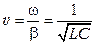
Определим коэффициент фазы b

,

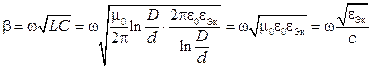где 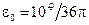– электрическая постоянная, Ф/м; 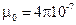– магнитная постоянная, Гн/м; 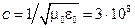– скорость электромагнитной волны в вакууме (скорость света в вакууме), м/с.

Скорость распространения электромагнитной волны в коаксиальном кабеле определится

.

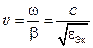Волновое сопротивление коаксиального кабеля определится по формуле

.

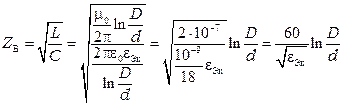Исследуем выражение коэффициента затухания коаксиальной пары. После подстановке первичных параметров в коэффициент затухания в металле 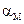получим

,

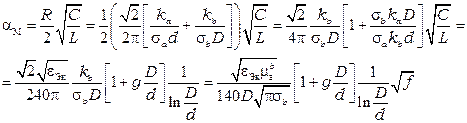где 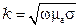; ; 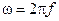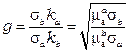. Для немагнитных материалов 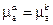и .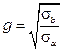

При подстановке первичных параметров в коэффициент затухания в диэлектрике 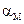получим

.

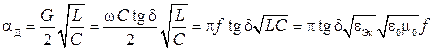Таким образом

.

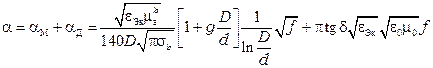Из этой формулы видно, потери в металлических элементах коаксиальной цепи изменяются пропорционально 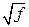, а потери в изоляции связаны с частотой линейным законом и с увеличение 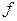возрастают значительно быстрее. При использовании высококачественных изоляционных материалов с малым 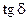можно добиться в определенном частотном диапазоне малых диэлектрических потерь и положить 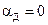; при более высоких частотах они настолько возрастают, что величина 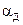играет доминирующую роль в общем затухании кабеля. В практически используемом спектре частот уплотнения коаксиальных кабелей (до 60×10⁶ Гц) при современных изоляционных материалах величина 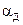незначительна и увеличение затухания происходит примерно пропорционально .

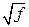При разработке любого типа кабеля всегда стоит задача создать оптимальную конструкцию, требующую минимальных затрат материалов и средств на изготовление и технологичную в производстве. При конструировании коаксиальных кабелей необходимо в первую очередь выбрать диаметры внутреннего и внешнего проводников кабеля и установить оптимальное соотношение. Как было сказано выше, затухание коаксиального кабеля с высококачественной изоляцией в практически используемом спектре частот (до 60 МГц) может быть определено (без учета потерь в изоляции) по следующей формуле

.

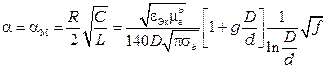Выразим соотношение 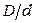через 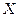. Из данного выражения следует, что с увеличением 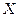его числитель растет линейно, а знаменатель пропорционален логарифму отношения диаметров. Пусть 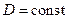, тогда изменение параметра 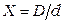будет достигаться изменением диаметра внутреннего проводника .

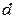Обозначим через 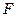выражение, входящее в формулу для 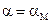и независящее от соотношения диаметров

.

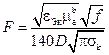Тогда

.

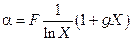Исследуем данное выражение на минимум затухания, взяв первую производную от 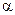по 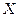и приравняв ее нулю

.

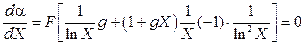Откуда получим, что 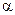минимально при соотношении

.

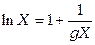Оптимальное соотношение диаметров проводников выполненных из меди ( 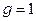) будет равным 3,6. Если внутренний проводник выполнен из меди, а внутренний из алюминия, то 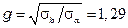и оптимальное соотношение диаметров будет равным 3,9. На рис. 3.28 приведены графики затухания коаксиальных цепей в зависимости от соотношения диаметров проводников. Из рис. 3.28 видно, что нарушение оптимального соотношения в меньшую сторону связано с довольно резким возрастанием коэффициента затухания. Поэтому выбирают отклонение соотношения диаметров 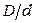в несколько большую сторону.

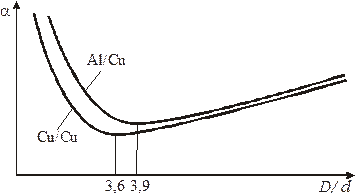
Рис. 3.28. Характер изменения затухания коаксиальных цепей в зависимости от соотношения диаметров
проводников

При замене медных проводников алюминиевыми затухание возрастает пропор­ционально соотношению активных сопротивлений или соответст­венно обратно пропорционально корню квадратному из проводимо­стей металлов 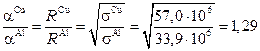, т.е. на 29 %. При замене только внешнего проводника на алюминиевый затухание возрастает всего на 6 %. Расход меди на производство коаксиального кабеля при этом сокращается на 65%.

Конструирование коаксиальной пары подчинено задаче созда­ния оптимальной ее конструкции, требующей минимальных затрат материалов и средств на изготовление. При этом в первую очередь необходимо выбрать диаметры внутреннего и внешнего проводни­ков кабеля и установить наиболее выгодное из соотношений при ис­пользовании различных металлов (медь, алюминий, биметалл).

При конструировании коаксиального кабеля приходится также отступать от оптимального отношения 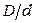, если величина волно­вого сопротивления кабеля строго нормирована. Например, для обеспечения 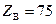Ом данное отношение 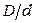определяется по формуле

.

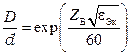Для получения норми­рованной величины 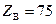Ом при оптимальном отношении 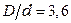необходимо иметь воздушно-пластмассовую изоляцию с малым содержанием диэлектрика ( 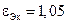). При повышенных значения 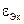приходится отступать от оптимальной конструкции кабеля. Так, при 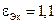приходится принять соотношение 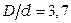, а при 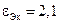– 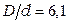. Таким образом, для междугородных кабелей связи, по которым необходимо обеспечить наибольшую дальность связи при выборе конструкции исходят из условия оптимального по затуханию соот­ношения ( 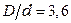) с учетом получения нормированной величины 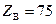Ом.