Зоновые (внутриобластные) коаксиальные кабели

Одно коаксиальный кабель ВКПАШп-1 (2,1/9,7) предназначен для организации зоновой связи с числом каналов равным 120 с расстоянием до 600 км. По кабелю организуется двухпроводные системы передачи: 60…552 кГц – в прямом направлении и 728…1320 кГц – в обратном.

Конструктивно кабель выполняется в двух вариантах подземный ВКПАШп-1 и подвесной с встроенным тросом ВКПАШпт-1. Длина пролета 50…65 м.

Внутренний проводник выполнен из медной проволоки диаметром 2,1, изоляция – из пористого полиэтилена с внешним диаметром 9,7 мм, внешний проводник – алюминиевая трубка толщиной 0,8 мм. Защитная оболочка выполнена из светостойкого полиэтилена толщиной 2,2 мм.

В конструкцию подвесного кабеля ВКПАШпт-1 общую полиэтиленовую оболочку вмонтирован стальной трос из 49 оцинкованных стальных проволок диаметром 0,34 мм. В поперечном сечении подвесной кабель имеет форму восьмерки. Разрывное усилие троса 6800 Н.

Имеется также бронированный вариант конструкции кабеля с кругло-проволочной броней.

Электрические характеристики кабеля ВКПА-1: сопротивление внутренней жилы постоянному току – 5,2 Ом/км; внешнего 2,6 Ом/км; емкость 56 мФ/км; номинальное волновое сопротивление 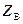=75 Ом.

2. Электродинамика направляющих систем

2.1 Основные положения. Основные уравнения электромагнитного поля

Электромагнитное поле (ЭМП) определяется как особый вид материи, характеризующийся возможностью распространения в вакууме со скоростью близкой к 3×10⁸ м/с, и оказывающей силовое воздействие на заряженные частицы.

ЭМП представляет собой единство двух своих составляющих – электрического и магнитного полей. Считают, что ЭМП определено, если в каждой точке пространства известны величины и направления четырех векторов:

Е – напряженности электрического моля, В/м;

D – электрического смещения Кл/м²;

В – магнитной индукции, Тл;

М – напряженности магнитного поля А/м.

Электрическое поле характеризуется силовым воздействием, как на неподвижные, так и движущиеся заряды. Магнитное поле характеризуется силовым воздействием лишь на движущиеся заряды. Электрические и магнитные поля связаны с определенными количествами э/м энергии.

Для векторов электромагнитного поля в вакууме справедливы соотношения:

; ,

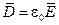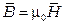где 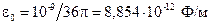– электрическая постоянная; 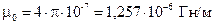– магнитная постоянная.

Среды, в которых распространяются электромагнитные волны, принято характеризовать макроскопическими параметрами, к которым относятся: e_а – абсолютная диэлектрическая проницаемость; m_а – абсолютная магнитная проницаемость; s – удельная проводимость. Для удобства сравнения свойств реальных сред с вакуумом вводят относительную проницаемости:

; .

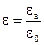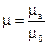Закон Ома в дифференциальной форме:

.

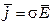Источником ЭМП являются свободные заряды и токи. Свободными считаются заряды, способные под воздействием электрического тока перемещаться на макроскопические расстояния (электроны в металлах, ионы в электролитах).

Основные уравнения ЭМП, называемые уравнениями Максвелла, обобщают два основных закона электродинамики, закон полного тока и закон э/м индукции.

Закон полного тока устанавливает количественное соотношение между вектором напряженности магнитного поля Н и электрическим током

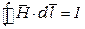. (2.1)

Согласно этому закону линейный интеграл напряженности магнитного поля по любому замкнутому контуру равен полному току, проходящему сквозь поверхность, ограниченную этим контуром. Ток I включает в себя ток проводимости и ток смещения (I = I_пр+ I_см). Данное уравнение называют первым уравнением Максвелла. Это уравнение количественно характеризует магнитное поле, возникающее при движении электричества и изменении электрического поля.

Закон э/м индукции открытый Фарадеем устанавливает соотношение между напряженностью электрического поля Е и магнитным потоком 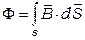. В соответствии с законом э/м индукции электродвижущая сила, возникает в контуре при изменении магнитного потока Ф, проходящего сквозь поверхность, ограниченную контуром, равна скорости изменения этого потока со знаком минус.

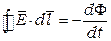. (2.2)

Это уравнение называют вторым уравнение Максвелла.

Поток электрического смещения 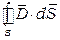через любую замкнутую поверхность равен электрическому заряду, заключенном внутри этой поверхности:

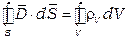, (2.3)

где 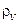– плотность электрического заряда.

Это соотношение из электростатики известно как теорема Гаусса. Оно устанавливает, что электрические заряды служат истоками и стоками электрического поля.

Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю. Линии вектора В замкнуты, либо уходят в бесконечность:

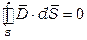. (2.4)

Из этого уравнения вытекает, что магнитные заряды в природе отсутствуют.

Уравнения (2.1)–(2.4) представлены в интегральной форме. Для решения практических задач большое значение имеют уравнения Максвелла, записанные в дифференциальной форме:

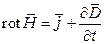, (2.5)

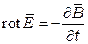, (2.6)

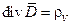, (2.7)

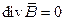, (2.8)

где 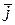– вектор плотности тока проводимости.

Уравнения Максвелла дополняются материальными уравнениями среды

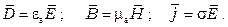
На границе между материальными телами параметры среды e, m, s скачкооб­разно изменяются. Согласно материальным уравнениям среды, испытывают скачки некоторые векторные поля.

Для решения задач электродинамики, помимо уравнений Максвелла, необходимо знать граничные условия – соотношения между векторами поля в двух очень близких точках, находящихся по обе стороны границы раздела двух сред. Граничные условия являются следствием уравнений Максвелла для этого особого случая. Особый интерес представляют границы разнородных сред, присутствующие в большинстве практических задач. Например, граница металл–диэлектрик (кабель, волновод), диэлектрик (e₁) – диэлектрик (e₂), волоконный световод и другие.

Рассмотрим отдельно граничные условия для электрических магнитных полей. При этом на границе имеют место быть, как нормальные (Е_n, Н_n), так и касательные (Е_t, Н_t) составляющие полей.

Для электрического поля на границе раздела двух сред имеет место равенство векторов электрического смещения для нормальных составляющих (D_1n= D_2n), и напряженности электрического поля для касательных составляющих (Е_1t= Е_2t).

Если на границе раздела сред расположен поверхностный заряд r_s, то нормальные составляющие векторов электрической индукции испытывают скачек на величину поверхностного заряда: D_1n – D_2n = r_s

Для магнитного поля на границе раздела сред имеется равенство векторов магнитной индукции для нормальных составляющих (B_1n= B_2n) и напряженности магнитного поля для касательных составляющих (H_1t= H_2t). При наличии поверхностного тока на границе раздела сред (j_s) касательная составляющая напряженности магнитного поля испытывает разрыв, равный его плотности: H_1t – H_2t = j_s

Таким образом, в общем случае граничные условия записываются:

D_1n – D_2n = r_s ; Е_1t = Е_2t;

B_1n= B_2n ; H_1t – H_2t = j_s .

В случае отсутствия поверхностных зарядов r_s и поверхностных токов j_s действует равенство всех приведенных компонент.

При изучении переменных ЭМП на поверхности металлических тел часто предполагают, что рассматриваемое тело является идеально проводящим (s = ¥). В этом случае напряженность электрического поля внутри проводника равна нулю. Тогда для проводящей среды, например второй D₂ = E₂ = B₂ = H₂ = 0 и выше приведенные уравнения примут вид: E_1t = 0; B_1n = 0; H_1t = j_s (соответственно Н_1n=0).

Энергия ЭМП

Запас электромагнитной энергии в объеме V определяется выражением:

,

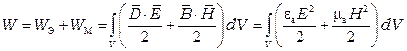где 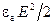– энергия электрического поля в единице объема; 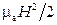– энергия магнитного поля в единице объема.

За изменение электромагнитной энергии в объеме отвечает теорема Умова–Пойтинга:

,

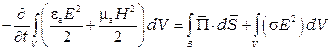где 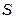– поверхность, ограничивающая объем V; 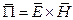– вектор Пойтинга.

Левая часть теоремы Умова–Пойтинга характеризует уход электромагнитной энергии из объема за единицу времени, правая – показывает, на что расходуется энергия, заключенная в объеме, за единицу времени. Первый член правой части представляет собой поток энергии, уходящий через замкнутую поверхность S объема V в единицу времени. Согласно закону Джоуля-Ленца второй член в правой части выражает энергию, преобра­зовываемую в тепло за единицу времени.

2.2. Метод комплексных амплитуд. Уравнения Максвелла в комплексной форме.
Однородные волновые уравнения для векторов E и H.

Все реальные электромагнитные процессы можно представить либо в виде суммы дискретных гармонических колебаний, либо в виде непрерывного спектра гармонических колебаний. Поэтому изучение гармонических электромагнитных полей представляет большой практический и теоретический интерес. Такие поля часто называют также монохроматическими.

Пусть вектор поля 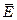изменяются по косинусоидальному закону, причем фазы всех трех прямоугольных проекций одинаковы, т.е. волна линейно поляризована, тогда выражение для 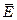запишется

,

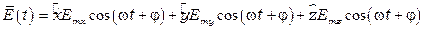где 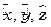– единичные вектора-орты по направлениям x, y, z, соответственно; 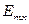, , 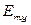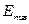– амплитуды; 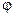– фаза; w – циклическая или круговая частота гармонических колебаний. Амплитуды и фаза не зависят от времени, а только от координат x, y, z.

Обозначим

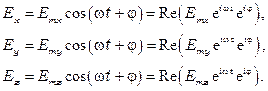
Комплексной амплитудой вектора 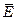назовем вектор

.

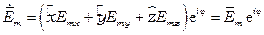Тогда мгновенное значение вектора 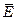определится по формуле

.

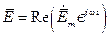Аналогично можно записать комплексную амплитуду напряженности магнитного поля

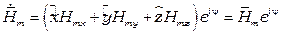
и мгновенное значение

.

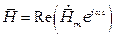Рассмотрим первое уравнение Максвелла

.

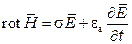Подставив вместо 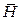величину 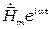, реальная часть которой равна 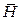, а вместо 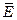величину 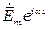, то получим

.

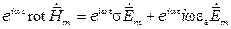После сокращения на 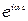получается первое уравнение Максвелла в комплексной форме записи (для комплексных амплитуд)

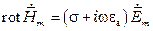
или

,

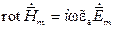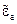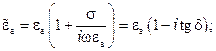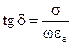где – комплексная д/э проницаемость, здесь –тангенс угла д/э потерь.

Аналогично получаются и остальные уравнения ЭМП в комплексной форме записи

,

,

.

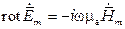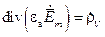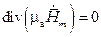Решив эти уравнения и определив комплексные амплитуды 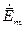и 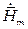, легко найти мгновенные значения векторов поля из соотношений

, .

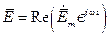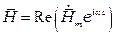Преимущество комплексной формы записи основных уравнений поля заключается в том, что время 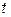исключается из этих уравнений, что значительно упрощает решение задач электродинамики.

В дальнейшем для упрощения записи при переходе к мгновенным значениям комплексные амплитуды будут обозначаться как

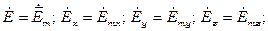
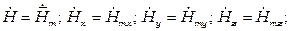
а без перехода к мгновенным значениям

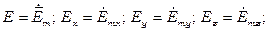
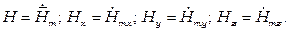
Уравнения Максвелла в комплексной форме записи в декартовой системе координат запишутся

, ,

, .

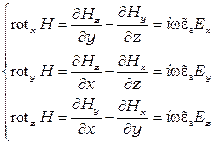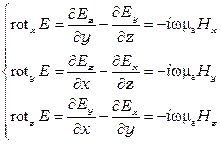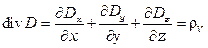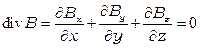Однородные волновые уравнения имеют вид (уравнения Гельмгольца)

, ,

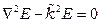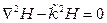где 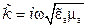– коэффициентом распространения в среде, 1/м.

В волновых уравнениях оператор 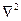называется лапласианом. Лапласиан от скалярной функции y в цилиндрической системе координат запишется:

.

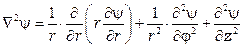Лапласиан от вектора является вектор. Его составляющими в декартовой системе координат является лапласиан от соответствующих компонент дифференци­руемого вектора:

.

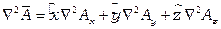В декартовой системе координат векторные волновые уравнения распада­ются на шесть независимых скалярных волновых уравнений:

.

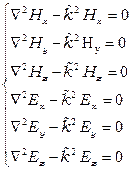Все эти уравнения имеют совершенно одинаковую форму. Поэтому для на­хождения составляющих ЭМП достаточно решить лишь одно уравнение в частных произ­водных, например:

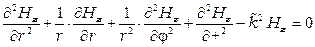
Остальные составляющие Е и Н определяются из 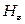непосредственно из уравнений Максвелла.

2.3. ЭМП в диэлектрике (we_а >> s)

Идеальный проводник – это среда с бесконечно большой удельной проводимостью 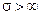, а идеальный проводник – это среда, не обладающая проводимостью 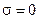. В идеальном проводнике может существовать только ток проводимости: 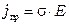, а в идеальном диэлектрике – только ток смещения: 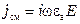. В реальных средах имеется как ток проводимости, так и ток смещения. Принято среду считать проводящей, когда: 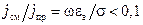. Диэлектрик характеризуется неравенством: .

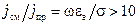Рассмотрим распространение гармонической электромагнитной энергии в идеальном диэлектрике (s = 0). Уравнения Максвелла для гармонических колебаний примут вид:

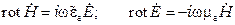
Волновые уравнения о декартовой системе координат получаются:

;

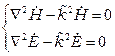здесь коэффициент распространения: .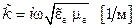

Рассмотрим распространение плоской э/м волны в однородном диэлектрике. Э/м волна называется плоской, когда все величины, характеризующие интенсивность э/м процесса, зависят только от одной декартовой координаты. Пусть волновой процесс распространяется вдоль оси z. Тогда поперечными по отношению к направлению распространения являются координаты x, y. При этом .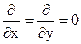

Решим уравнение Гемгольца для вектора 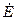. Примем, что 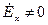, а 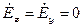. Следовательно 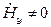, а .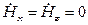

Тогда волновые уравнения для компонент 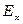и 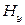запишутся

; .

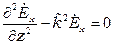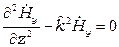Решим волновое уравнение относительно 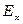. Общим решением этого уравнения является суперпозиция двух частных решений

,

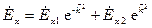где 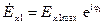– прямая волна; 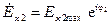– обратная волна.

Коэффициент распространения можно записать

,

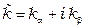где 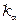– называется коэффициентом затухания волны в среде; 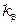– называется коэффициентом фазы волны в среде.

Для идеального диэлектрика 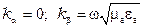. Здесь 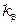называют волновым числом. Таким образом

.

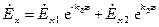Мгновенное значение напряженности электрического поля запишется:

.

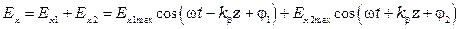Первое слагаемое здесь называется прямой волной, а второе - обратной.

Есл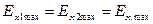и и 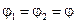, то получается стоячая волна (см. рис. 2.1)

.

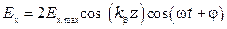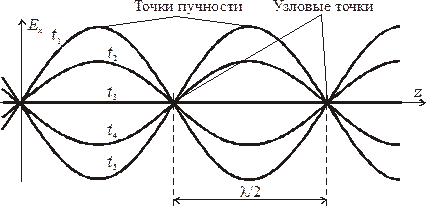
Рис. 2.1. Стоячая волна

Пусть обратная волна отсутствует, тогда изменение бегущей волны определяется по формуле:

.

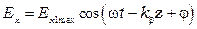На рис. 2.2 представлено распределение бегущей волны Е_х для двух моментов времени t₁ и t₂ = t₁ + Dt.

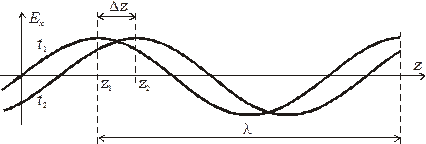
Рис 2.2. Распределение бегущей волны Е_х в моменты времени t₁ и t₂

Скорость перемещения фронта бегущей волны называется фазовой скоростью и определяется из условия равенства фаз двух косинусоид (см. рис. 2.2):

,

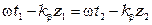Откуда

.

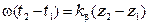Тогда

,

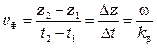поскольку 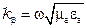, тогда получаем:

,

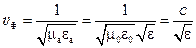где 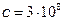– скорость электромагнитной волны в вакууме (скорость света в вакууме), м/с.

Расстояние при прохождении которого волна изменяет стою фазу на 2p, называется длиной волны и определяется из равенства:

.

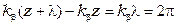Тогда

.

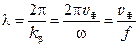Напряженность магнитного поля 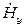определяется из уравнения Максвелла

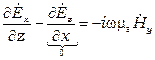
откуда

.

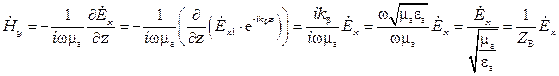Здесь 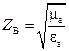– называется волновым сопротивлением.

Для вакуума m = e = 1; Z_В= 376,8 Ом

В общем случае волновое сопротивление комплексная величина.

2.4. ЭМП в диэлектрике (s>>we_а)

Рассмотрим распространение плоской волны в проводящей среде.

Волновое уравнение для напряженности электрического поля 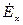запишется:

.

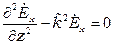Определим :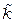

.

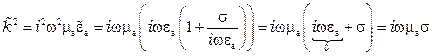Тогда

.

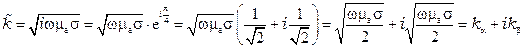Таким образом:

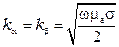
Фазовая скорость электромагнитной волны в проводнике определится по формуле:

.

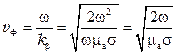Длина волны электромагнитной волны в проводнике определится по формуле:

.

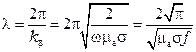Решением волнового уравнения является:

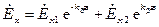
Рассмотрим только прямую волну:

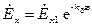
Мгновенное значение напряженности электрического поля запишется:

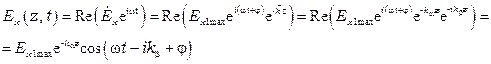
Волна затухающая. Затухание амплитуды пропорционально .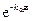

Глубиной проникновения Q называется такое расстояние от поверхности проводящей среды, на котором амплитуда волны уменьшается в 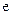раз.

Величина Q определяется из соотношения:

,

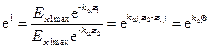Тогда

.

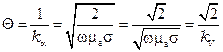Здесь: 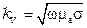– коэффициент вихревых токов.

На рис. 2.3 представлено изменение глубины проникновения в проводящей среде от частоты.

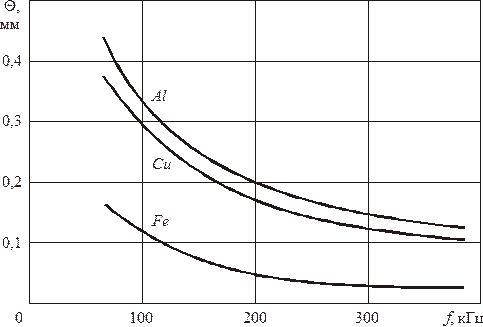
Рис 2.3. Зависимость глубины проникновения в проводящей среде от частоты

Составляющая 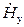определяется из уравнения Максвелла:

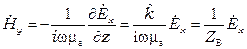
Здесь: .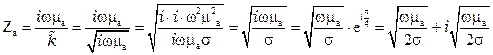

2.5. Классы электромагнитных волн направляющих систем. Исходные принципы
расчета направляющих систем

Классы электромагнитных волн направляющих систем

Характер распространения электромагнитных волн в направляющих системах, структура поля и свойства систем зависят, прежде всего, от типа волны, используемой для передачи энергии.

Существуют следующие классы волн:

1) ТЕМ – поперечно-электромагнитная волна;

2) Е – электрическая волна (или ТМ – поперечно-магнитная);

3) Н – магнитная волна (или ТЕ – поперечно-электрическая);

4) ЕН, НЕ – гибридные смешанные волны (дипольные волны).

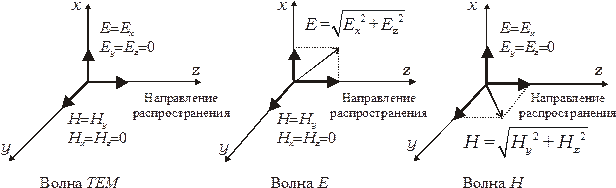
Рис. 2.4. Характеристика электромагнитных волн направляющих систем.
В направлении оси z происходит распространение волны.

Волна ТЕМ содержит только поперечные составляющие поля (продольные составляющие Е_z и Н_z равны нулю), т.е. линии полей Е и Н целиком лежат в поперечных плоскостях и в точности повторяют картину линий поля при статическом напряжении и постоянном токе. Волна ТЕМ существует лишь в линиях, содержащих не менее двух изолированных проводников, находящихся под разными потенциалами. Она используется при передаче энергии в сравнительно ограниченном диапазоне частот по проводным системам, где определяющими являются токи проводимости I_пр, в частности при передаче по симметричным коаксиальным цепям.

Волны Е и Н содержат, кроме поперечных электромагнитных волн (Е_^ и Н_^) по одной продольной составляющей поля, для волн Е поле Е_z ¹ 0 и для волн Н поле Н_z ¹ 0. Поэтому их силовые линии располагаются как в поперечных, так и в продольных сечениях направляющих систем. Продольные составляющие электрического и магнитных полей задают направление движения энергии вдоль линии. Эти волны возбуждаются в весьма высоком диапазоне частот, где определяющими являются токи смещения I_см. Они используются при передаче энергии по металлическим и диэлектрическим волноводам. Процесс передачи основных волн связан с потенциальным полем, а волн высшего порядка Е и Н с вихревыми полями. По волноводу передаются лишь очень короткие волны. Длина волн должна быть такой, чтобы в сечении волновода их уложилось целое число полуволн или хотя бы одна полуволна.

Гибридные или смешанные волны представляют собой сумму волн Е и Н и содержит до шести компонентов поля, в том числе обе продольные составляющие Е_z и Н_z. К числу смешанных волн относятся волны, передаваемые и диэлектрическими волноводами. Гибридные смешанные волны разделяются на два типа. НЕ – с преобладанием в поперечном сечении поля Н, и ЕН - с преобладанием в поперечном сечении поля Е.

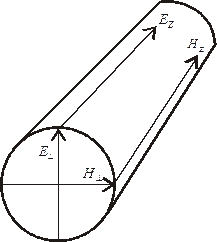
Рис 2.5. Цилиндрический проводник

Исходные принципы расчета направляющих систем.

Уравнения Максвелла дают возможность решить практически любую электродинамическую задачу, включая передачу сигналов связи по различным направляющим системам в различных диапазонах частот. Однако во многих случаях крайне сложно, а подчас и нецелесообразно искать точные решения на базе электродинамики. Существуют приближенные методы решения задач различных классов. Наиболее характерными методами, которые можно считать предельными для электродинамики, явились методы теории электрических цепей и геометрической оптики. В первом случае совершается переход от волновых процессов к колебательным (длина волны l >> D), а во втором - к лучевым (геометрическим) процессам
l << D.

В зависимости от соотношения длины волны и поперечных геометриче­ских размеров D системы можно подразделить на три режима передачи.

1) Квазистационарный режим при l >> D, соответствующий низкочастотному диапазону (l ® ¥). В этом случае передача ведется на поперечно-электромагнитной волне ТЕМ. Здесь волновые уравнения ЭМП вырождаются в уравнения электромагнитостатики и решаются с помощью законов Ома и Кирхгофа, и обычных телеграфных уравнений теории цепей. Это справедливо для частот до 10⁸ ¸ 10⁹ Гц. В данном режиме осуществляется передача по двухпроводным линиям связи: воздушным линиям, симметричным и коаксиальным кабелям.

2) Электродинамический (резонансный) режим при l » D, соответствую­щий волновым процессам, описываемым полными уравнениями электродина­мики – уравнениями Максвелла. В этом режиме передача ведется по направляю­щим системам на волнах типа Е и Н. К таким направляющим системам относятся волноводы, линии поверхностной волны, а также коаксиальные кабели при передачах на сверхвысоких частотах 10¹⁰ ¸ 10¹² Гц (сантиметро­вый и миллиметровый диапазоны). Одномодовые световоды также работают в этом режиме (микронные волны). Этот режим наиболее сложен для исследования, т.к. здесь имеют место резонансные процессы (l»D).

3) В квазиоптическом режиме действуют законы геометрической (лучевой) и волновой оптики. Здесь приходится иметь дело с лазерными системами, диэлектрическими волноводами, световодами, работающими на смешанных гибридных волнах (ЕМ или НЕ) и симметричных волнах Е_0n, Н_0n в оптическом диапазоне 10¹³ ¸ 10¹⁵ Гц (микронные волны).

3 Двухпроводные направляющие системы.

3.1 Основное уравнение однородной кабельной цепи

По физической природе параметры кабеля аналогичны параметрам колебательных контуров, составленных из элементов R, L, и C. Разница состоит лишь в том, что в контурах эти параметры (R, L и C) являются сосредоточенными, а в кабелях они равномерно или неравномерно распределены по всей длине цепи. Если параметры линии распределены равномерно, то такая линия называется однородной, иначе – неоднородной. В общем случае электрическая схема замещения двухпроводной цепи с распределенными параметрами имеет вид, представленный на рис. 3.1. Здесь: 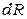– сопротивление токопроводящих жил участка цепи длиной 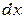; 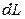– индуктивность участка цепи длиной 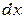; 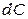– емкость участка цепи длиной 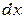; 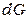– проводимость изоляции участка цепи длиной .

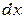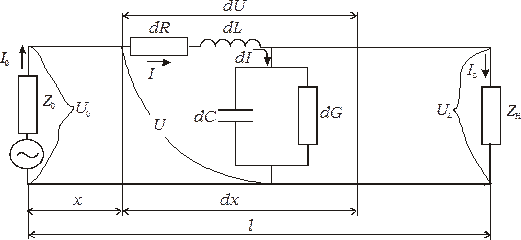
Рис 3.1. Электрическая схема замещения двухпроводной цепи связи

В начале цепи включен генератор с внутренним сопротивлением Z₀, в конце – нагрузка Z_Н. Обозначим напряжение и ток в начале цепи U₀, I₀, в конце – U_l, I_l.

Обозначим силу тока, протекающего по элементу цепи dx, через I и напряжение между проводниками через U. Падение напряжения и утечка тока на участке dx будет определяться по формулам:

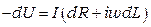, (3.1)

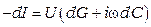. (3.2)

Уравнения (3.1), (3.2) называются телеграфными уравнениями. Знак «–» в этих уравнениях означает, что при продвижении электромагнитной волны по двухпроводной цепи от начала к концу амплитуда напряжения и тока падает.

Для однородных линий можно записать 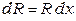, , 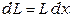, 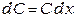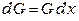. Параметры 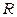, , 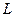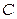и 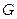называются первичными параметрами цепи. Качество передачи по кабельным линиям связи и их электрические свойства полностью характеризуются: активным сопротивлением R, индуктивностью L, емкостью C и проводимостью изоляции G. Эти параметры определяются конструкцией кабеля, используемыми материалами и частотой тока.

Параметры R и L, включенные последовательно, образуют суммарное сопротивление 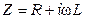, а параметры G и C – суммарную проводимость 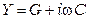. Из указанных четырех первичных параметров кабеля лишь R и G обуславливают потери энергии: R – потери на тепло в ТПЖ и других металлических частый кабеля (экран, оболочка, брони); G – потери в изоляции.

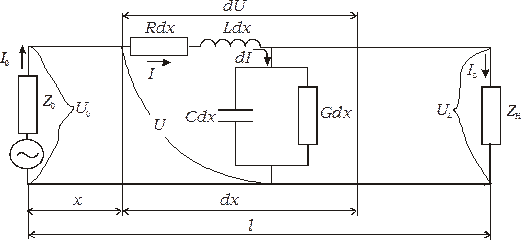
Рис 3.2. Электрическая схема замещения однородной двухпроводной цепи связи

Таким образом, уравнения (3.1), (3.2) для однородной цепи будут иметь вид

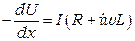, (3.3)

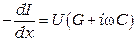. (3.4)

Для решения этих уравнений относительно U и I исключим сначала I из (3.3), взяв вторую производную:

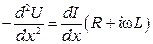. (3.5)

Подставим (3.4) в (3.5), получим:

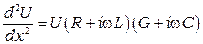. (3.6)

Обозначим:

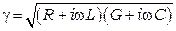. (3.7)

Тогда:

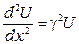. (3.8)

Здесь 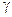– коэффициент распространения двухпроводной цепи, 1/м.

Решение (3.8) имеет вид:

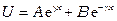. (3.9)

После дифференцирования уравнения (3.9) и подстановки в (3.3), получим выражение для тока:

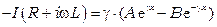. (3.10)

Обозначим

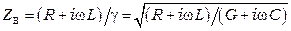. (3.11)

Здесь: 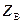– волновое сопротивление, Ом.

Тогда

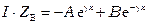. (3.12)

Таким образом, имеется два уравнения с двумя неизвестным А и В:

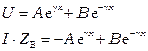. (3.13)

Для нахождения постоянных А и В воспользуемся значениями тока и напряжения в начале цепи (при x = 0) I₀ и U₀. Тогда уравнения (3.13) примут вид:

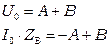. (3.14)

Отсюда:

. (3.15)

Подставив значение А и В в (3.13), получаем:

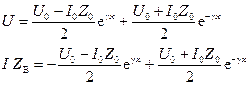, (3.16)

Уравнения (3.16) можно представить в другом виде. С учетом того, что получим:

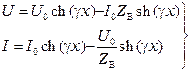. (3.17)

В конце цепи при x = l получим:

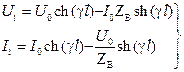. (3.18)

Практически, оказывается, удобно пользоваться выражениями, устанавливающими зависимость напряжения и тока вначале цепи от напряжения и тока в конце цепи. Решив (3.19) относительно U₀ и I₀, получим:

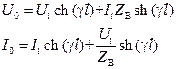. (3.19)

Уравнения (3.16) – (3.19) устанавливают взаимосвязь токов и напряжений с параметрами цепи R, L, C и G или 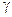и Z_B, позволяя определить напряжение и ток в любой точке цепи. Эти уравнения справедливы при любых нагрузках Z₀ и Z_Н.

При согласованных нагрузках (Z₀ = Z_Н =Z_B) U₀/I₀ = U_l/I_l = Z_B уравнения (3.16) – (3.19) упрощаются и принимают вид:

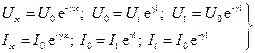(3.20)

Практически наиболее часто пользуются уравнениями в виде:

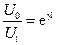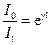; . (3.21)

В этом случае отношение мощностей в начале и конце линии имеет вид:

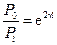. (3.22)

Таким образом, получены уравнения однородной кабельной цепи в общем виде при любых нагрузках по концам и при согласованных нагрузках.

Из приведенных формул следует, что распространение энергии по линии, ток и напряжение в любой точке цепи обусловим двумя параметрами 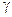и Z_B.

3.2 Вторичные параметры двухпроводных направляющих систем

Вторичными параметрами линии являются волновое сопротивление Z_B и коэффициент распространения g. Они широко используются для оценки эксплуатационно-технических качеств линии связи. При проектировании, сооружении и эксплуатации кабельных линий в первую очередь корректируются и контролируются именно вторичные параметры линии.

3.2.1 Волновое сопротивление

Волновое сопротивление Z_B – это сопротивление, которое встречает электромагнитная волна при распространении вдоль однородной линии без отражения, т.е. при условии отсутствия влияния на процесс передачи несогласованности нагрузок по концам линии. Волновое сопротивление свойственно данному типу кабеля и зависит лишь от его первичных параметров и частоты передаваемого тока.

Количественное соотношение, имеющее место между волной напряжения и волной тока в линии, и есть волновое сопротивление цепи. При этом, как следует из данного определения волнового сопротивления, необходимо рассматривать лишь падающую (движущуюся вперед) электромагнитную волну:

.

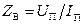Если в линии выделить отдельно отраженную волну, то она, двигаясь к началу линии, также будет встречать сопротивление, равное волновому:

.

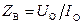Волновое сопротивление рассчитывается по формуле:

.

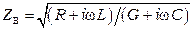По всей физической природе, что также следует и из приведенной формулы, волновое сопротивление Z_B не зависит от длины кабельной линии и для однородной линии постоянно в любой точке цепи.

Выражение для волнового с