Уравнения в полных дифференциалах.
Если левая часть дифференциального уравнения первого порядка
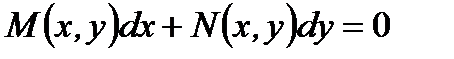 (7.91)
(7.91)
где 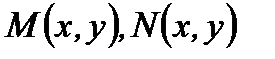 непрерывные функции со своими непрерывными частными производными, является полным дифференциалом некоторой функции
непрерывные функции со своими непрерывными частными производными, является полным дифференциалом некоторой функции 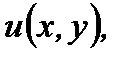 то есть
то есть
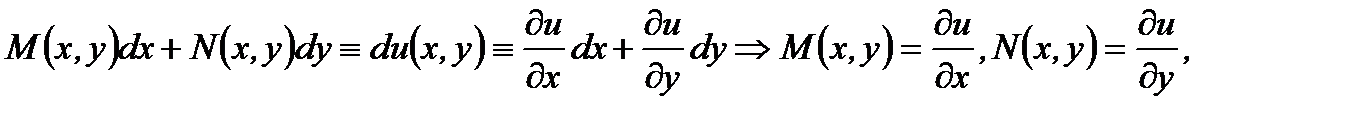 (7.92)
(7.92)
то оно называется уравнением в полных дифференциалах.
Необходимым и достаточным условием того, чтобы уравнение (7.91) было уравнением в полных дифференциалах, является выполнение соотношения
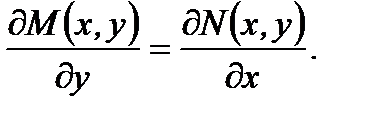 (7.93)
(7.93)
Итак, если уравнение (7.91) есть уравнение в полных дифференциалах, то оно эквивалентно уравнению 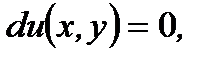 интегрирование которого дает нам общее решение (7.91) в виде
интегрирование которого дает нам общее решение (7.91) в виде
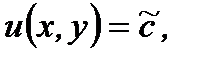 (7.94)
(7.94)
где 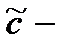 произвольная постоянная.
произвольная постоянная.
Теперь перейдем к нахождению функции 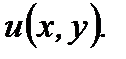 Для этого сначала интегрируем, например, уравнение
Для этого сначала интегрируем, например, уравнение 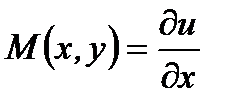 по
по 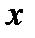 (
( 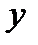 при этом считается постоянным параметром)
при этом считается постоянным параметром)
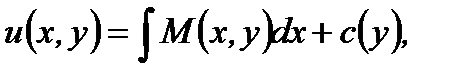 (7.95)
(7.95)
а потом подставляем (7.95) в уравнение 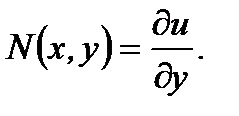 В результате получим
В результате получим
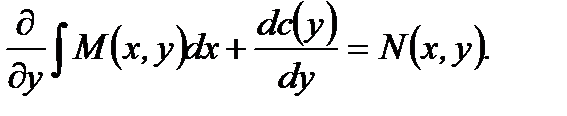 (7.96)
(7.96)
Из (7.96) путем интегрирования по 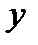 (
( 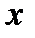 при этом считается постоянным параметром) находим функцию
при этом считается постоянным параметром) находим функцию 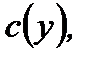 а, следовательно, находим и искомую функцию
а, следовательно, находим и искомую функцию 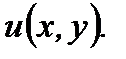 Далее, подставляя найденное выражение для
Далее, подставляя найденное выражение для 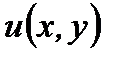 в (7.94), получим общее решение дифференциального уравнения в полных дифференциалах (7.91).
в (7.94), получим общее решение дифференциального уравнения в полных дифференциалах (7.91).
Пример 7.17.Решить уравнение
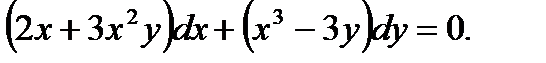 (7.97)
(7.97)
Решение.Поскольку
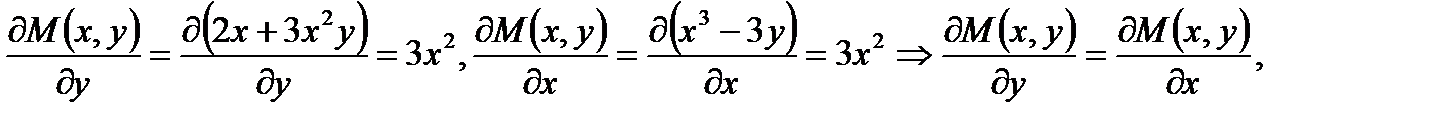 (7.98)
(7.98)
то данное уравнение является уравнением в полных дифференциалах. Интегрируя уравнение
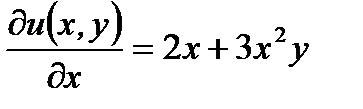 (7.99)
(7.99)
по переменной 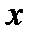 (
( 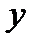 постоянный параметр), получим
постоянный параметр), получим
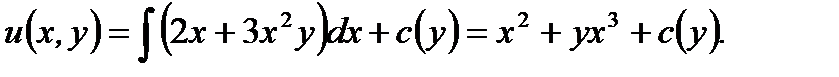 (7.100)
(7.100)
Подставляя полученное выражение для 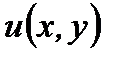 в уравнение
в уравнение
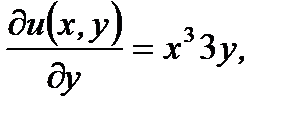 (7.101)
(7.101)
получим
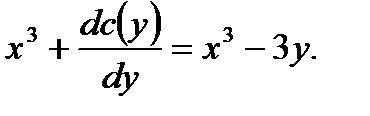 (7.102)
(7.102)
Отсюда
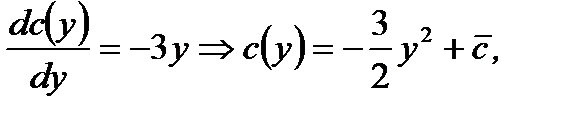 (7.103)
(7.103)
где 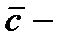 произвольная постоянная. Таким образом, согласно (7.94) с учетом (7.100) и (7.103) общее решение исходного уравнения (7.97) имеет вид
произвольная постоянная. Таким образом, согласно (7.94) с учетом (7.100) и (7.103) общее решение исходного уравнения (7.97) имеет вид
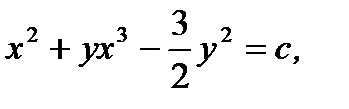 (7.104)
(7.104)
где 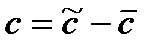 есть новая произвольная постоянная.
есть новая произвольная постоянная.
Ответ: 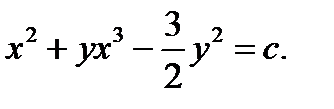
Дата добавления: 2021-05-28; просмотров: 416;











