Линейные неоднородные уравнения первого порядка.
Дифференциальное уравнение вида
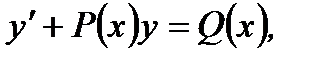 (7.49)
(7.49)
где 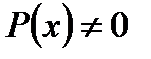 и
и 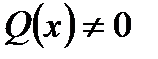 непрерывные функции, называется линейным неоднородным уравнением первого порядка (линейным, так как
непрерывные функции, называется линейным неоднородным уравнением первого порядка (линейным, так как 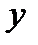 и
и 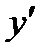 входят в уравнение в первых степенях, неоднородным, так как правая часть уравнения не равна нулю). При
входят в уравнение в первых степенях, неоднородным, так как правая часть уравнения не равна нулю). При 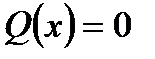 уравнение (7.49) принимает вид
уравнение (7.49) принимает вид
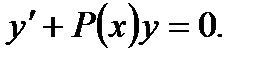 (7.50)
(7.50)
Последнее называется линейным однородным уравнением первого порядка и представляет собой уравнение с разделяющимися переменными. Его общее решение
имеет вид
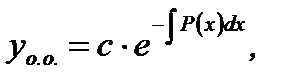 (7.51)
(7.51)
где 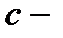 произвольная постоянная.
произвольная постоянная.
Как известно из теории линейных дифференциальных уравнений, общее решение линейного неоднородного уравнения 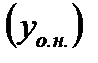 складывается из общего решения соответствующего однородного уравнения (7.50)
складывается из общего решения соответствующего однородного уравнения (7.50) 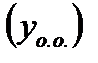 и одного частного решения неоднородного уравнения (7.49)
и одного частного решения неоднородного уравнения (7.49) 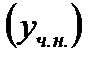 , то есть
, то есть
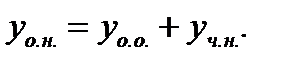 (7.52)
(7.52)
Для нахождения 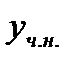 применяем метод вариации произвольной постоянной. Суть метода состоит в том, что одно частное решение неоднородного уравнения ищем в виде (7.51), считая
применяем метод вариации произвольной постоянной. Суть метода состоит в том, что одно частное решение неоднородного уравнения ищем в виде (7.51), считая  неизвестной функцией от
неизвестной функцией от 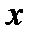 (варьируем постоянную
(варьируем постоянную  ), то есть
), то есть
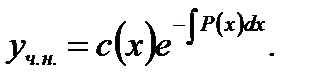 (7.53)
(7.53)
Подставляя (7.53) в (7.49), для определения функции 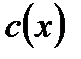 получим дифференциальное уравнение первого порядка с разделяющимися переменными
получим дифференциальное уравнение первого порядка с разделяющимися переменными
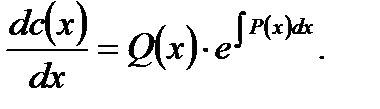 (7.54)
(7.54)
Решая последнее с учетом того, что произвольная постоянная, появившаяся после интегрирования, равна нулю (нам нужно одно частное решение), получим выражение для 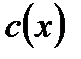 . Подставляя найденное выражение для
. Подставляя найденное выражение для 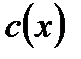 в (7.53) и учитывая (7.52), получим общее решение неоднородного линейного уравнения первого порядка (7.49).
в (7.53) и учитывая (7.52), получим общее решение неоднородного линейного уравнения первого порядка (7.49).
Пример 7.13.Найти частное решение линейного неоднородного уравнения, пользуясь методом вариации постоянной
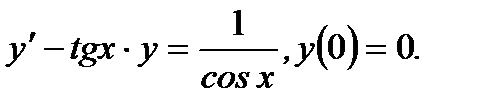 (7.55)
(7.55)
Решение.Решая сначала соответствующее однородное уравнение
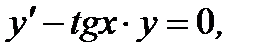 (7.56)
(7.56)
получим
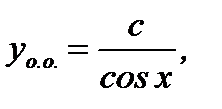 (7.57)
(7.57)
где 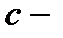 произвольная постоянная. Одно частное решение неоднородного уравнения (7.55) ищем методом вариации постоянной в виде
произвольная постоянная. Одно частное решение неоднородного уравнения (7.55) ищем методом вариации постоянной в виде
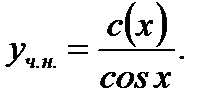 (7.58)
(7.58)
Подставляя (7.58) в (7.55) и учитывая, что
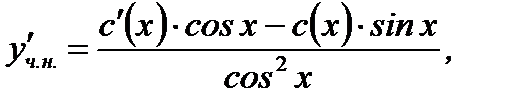 (7.59)
(7.59)
получим
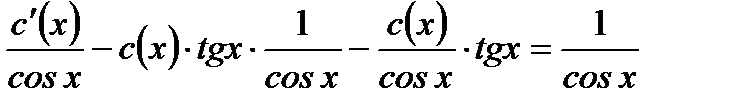 (7.60)
(7.60)
или
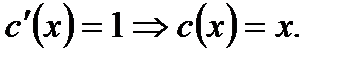 (7.61)
(7.61)
Тогда согласно (7.58) имеем
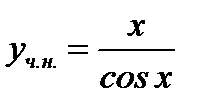 (7.62)
(7.62)
и, следовательно (см. (7.52)), общее решение исходного уравнения имеет вид
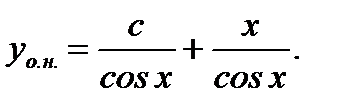 (7.63)
(7.63)
Из общего решения (7.63) выделим частное решение исходного уравнения, имея в виду
начальное условие Коши 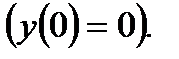 Имеем
Имеем 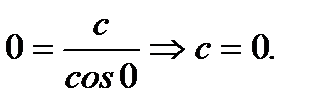 Таким образом, решение задачи Коши имеет вид
Таким образом, решение задачи Коши имеет вид
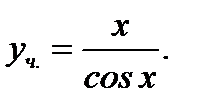 (7.64)
(7.64)
Ответ: 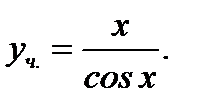
Отметим, что общее решение линейного неоднородного уравнения первого порядка можно найти и методом Бернулли. Суть этого метода состоит в том, что решение уравнения (7.49) ищем в виде
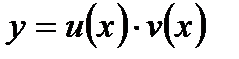 (7.65)
(7.65)
считая, что функция 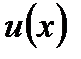 является решением соответствующего однородного уравнения
является решением соответствующего однородного уравнения
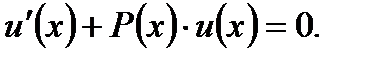 (7.66)
(7.66)
Подставим (7.65) в уравнение (7.49). После некоторых преобразований, получим
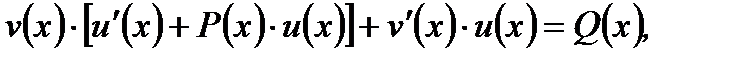 (7.67)
(7.67)
или с учетом (7.66)
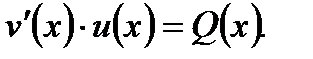 (7.68)
(7.68)
Решая уравнение (7.66), определим 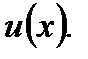 Найденное выражение
Найденное выражение 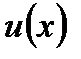 подставим в (7.68). Интегрируя последнее, найдем функцию
подставим в (7.68). Интегрируя последнее, найдем функцию 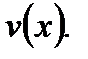 Подставляя найденные функции
Подставляя найденные функции 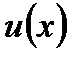 и
и 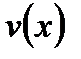 в (7.65), получим общее решение исходного уравнения (7.49).
в (7.65), получим общее решение исходного уравнения (7.49).
Пример 7.14.Найти общее решение линейного неоднородного уравнения
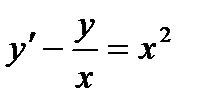 , (7.69)
, (7.69)
пользуясь методом Бернулли.
Решение.Полагая 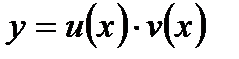 и учитывая, что
и учитывая, что 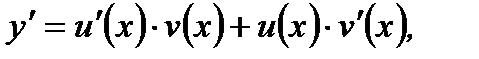 уравнение (7.69) преобразуем к виду
уравнение (7.69) преобразуем к виду
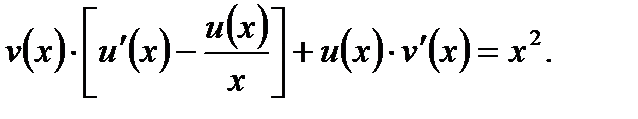 (7.70)
(7.70)
Согласно (7.66) имеем
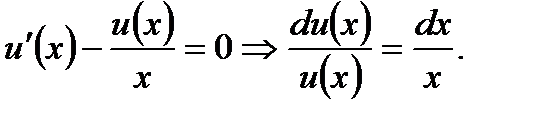 (7.71)
(7.71)
Интегрируя последнее, получим
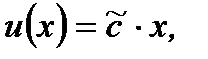 (7.72)
(7.72)
где 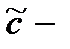 произвольная постоянная. Подставляя (7.72) в (7.70), получим
произвольная постоянная. Подставляя (7.72) в (7.70), получим
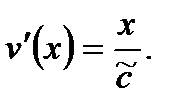 (7.73)
(7.73)
Отсюда
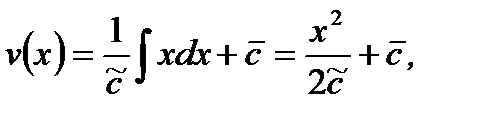 (7.74)
(7.74)
где 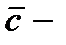 произвольная постоянная. Таким образом, общее решение уравнения (7.69) имеет вид
произвольная постоянная. Таким образом, общее решение уравнения (7.69) имеет вид
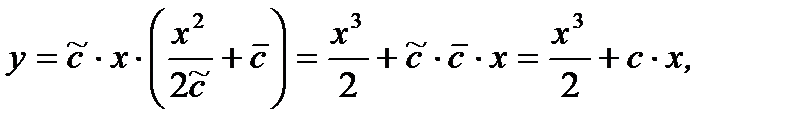 (7.75)
(7.75)
где 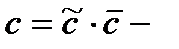 новая произвольная постоянная.
новая произвольная постоянная.
Ответ: 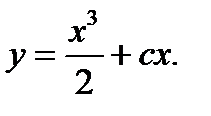
Дата добавления: 2021-05-28; просмотров: 459;











