Дифференциальные уравнения
Дифференциа́льное уравне́ние — уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами). Порядок входящих в уравнение производных может быть различен (формально он ничем не ограничен). Производные, функции, независимые переменные и параметры могут входить в уравнение в различных комбинациях или все, кроме хотя бы одной производной, отсутствовать вовсе. Дифференциальное уравнение порядка выше первого можно преобразовать в систему уравнений первого порядка, в которой число уравнений равно порядку исходного уравнения.
Порядок, или степень дифференциального уравнения — наивысший порядок производных, входящих в него.
Решением (интегралом) дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные 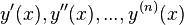 до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Задача об интегрировании дифференциального уравнения считается решённой, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде через известные функции или нет.
до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Задача об интегрировании дифференциального уравнения считается решённой, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде через известные функции или нет.
Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных.
В зависимости от комбинаций производных, функций, независимых переменных дифференциальные уравнения подразделяются на линейные и нелинейные, с постоянными или переменными коэффициентами, однородные или неоднородные. В связи с важностью приложений в отдельный класс выделены квазилинейные (линейные относительно старших производных) дифференциальные уравнения в частных производных.
Решения дифференциальных уравнений подразделяются на общие и частные решения. Общие решения включают в себя неопределенные постоянные, а для уравнений в частных производных — произвольные функции от независимых переменных, которые могут быть уточнены из дополнительных условий интегрирования (начальных условий для обыкновенных дифференциальных уравнений, начальных и граничных условий для уравнений в частных производных). После определения вида указанных постоянных и неопределенных функций решения становятся частными.
Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения, зависящие от одной независимой переменной; они имеют вид
F(x,y,  или F(x,y,
или F(x,y, 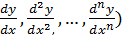
где 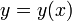 — неизвестная функция, зависящая от независимой переменной
— неизвестная функция, зависящая от независимой переменной 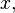 штрих означает дифференцирование по
штрих означает дифференцирование по 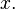 Число
Число 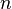 называется порядком дифференциального уравнения. Наиболее практически важными являются дифференциальные уравнения первого и второго порядка.
называется порядком дифференциального уравнения. Наиболее практически важными являются дифференциальные уравнения первого и второго порядка.
Дифференциальное уравнение первого порядка.
Содержат:1) независимую переменную х; 2) зависимую переменную у (функцию); 3) первую производную функции: 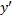 .
.
Решить дифференциальное уравнение – это значит, найти множество функцийy=f(x)+C, которые удовлетворяют данному уравнению. Такое множество функций называется общим решением дифференциального уравнения.
Пример 1
1. Решить дифференциальное уравнение 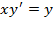
В первую очередь нужно переписать производную немного в другом виде. Вспоминаем громоздкое обозначение производной: 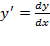 .
.
Итак, на первом этапе переписываем производную в нужном нам виде:
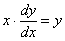
На втором этапе всегда смотрим, нельзя ли разделить переменные? Что значит разделить переменные? Грубо говоря, в левой части нам нужно оставить только «игреки», а в правой части организовать только «иксы». Разделение переменных выполняется с помощью «школьных» манипуляций: вынесение за скобки, перенос слагаемых из части в часть со сменой знака, перенос множителей из части в часть по правилу пропорции и т.п.
Дифференциалы dy и dx – это полноправные множители и активные участники боевых действий. В рассматриваемом примере переменные легко разделяются перекидыванием множителей по правилу пропорции: 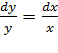
Переменные разделены. В левой части – только «игреки», в правой части – только «иксы».
Переменные разделены. В левой части – только «игреки», в правой части – только «иксы».
Следующий этап – интегрирование дифференциального уравнения. Всё просто, навешиваем интегралы на обе части: 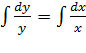
Решениеv дифференциального уравнения является 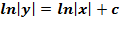 ,то есть, – это общий интеграл или можно так представить: ln
,то есть, – это общий интеграл или можно так представить: ln 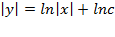
Представим функцию в явном виде: ln 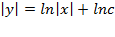 или
или 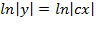 или у=Сх
или у=Сх
Пример 2
Найти частное решение дифференциального уравнения 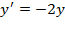 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 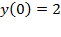
По условию требуется найти частное решение, удовлетворяющее начальному условию. Такая постановка вопроса также называется задачей Коши.
Сначала находим общее решение. В уравнении нет переменной «икс», но это не должно смущать, главное, в нём есть первая производная.
Переписываем производную в нужном виде: 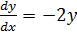
Очевидно, что переменные можно разделить: 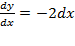
Интегрируем уравнение:
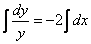
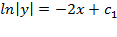
Общий интеграл получен. Здесь константа помечена индексом 1. но её легко преобразовать в другую константу. В данном случае можно записать y= 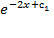 или
или 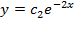
На завершающем этапе нужно найти частное решение, удовлетворяющее заданному начальному условию 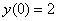 . В чём состоит задача? Необходимо подобрать такое значение константы
. В чём состоит задача? Необходимо подобрать такое значение константы 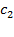 , чтобы выполнялось заданное начальное условие y
, чтобы выполнялось заданное начальное условие y 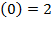 .
.
Оформить можно по-разному, но понятнее всего, пожалуй, будет так. В общее решение вместо «икса» подставляем ноль, а вместо «игрека» двойку, т.е. 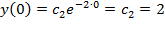
В общее решение 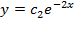 подставляем найденное значение константы
подставляем найденное значение константы 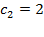
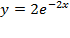 – это и есть нужное нам частное решение.
– это и есть нужное нам частное решение.
Пример 3
Решить дифференциальное уравнение 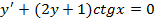
Решение: Переписываем производную в нужном нам виде:
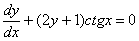
Оцениваем, можно ли разделить переменные? Можно. Переносим второе слагаемое в правую часть со сменой знака:
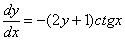
Перекидываем множители по правилу пропорции:
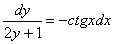
Переменные разделены, интегрируем обе части:
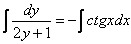
Интеграл левой части легко найти методом подведения функции под знак дифференциала, с интегралом от котангенса расправляемся стандартным приемом, переписываем его как отношение cosx на sinx:
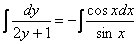
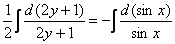
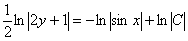
В правой части у нас получился логарифм, согласно технической рекомендации, в этом случае константу тоже следует записать под логарифмом.
Теперь пробуем упростить общий интеграл. Поскольку у нас одни логарифмы, то от них вполне можно (и нужно) избавиться. Максимально «упаковываем» логарифмы. И получаем решение в виде: 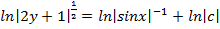 или окончательно общее решение
или окончательно общее решение 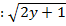 =
= 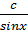
Дата добавления: 2016-06-05; просмотров: 3670;











