Поправка за высоту точки стояния прибора.

Наблюдения с гравиметром обычно проводятся на неровном рельефе земной поверхности. При этом значение силы тяжести зависит от высоты точки наблюдения – с увеличением высоты значения силы тяжести уменьшается. Для того, чтобы рельеф поверхности наблюдения не вносил ошибок в наблюденные данные, результаты гравиметрической съемки приводят к уровню моря (или редуцируют на уровень моря). Если представить себе, что между уровнем моря и поверхностью наблюдения нет горных пород, а находится только воздух, то, учитывая формулу нормального вертикального градиента силы тяжести Vzz, зависимость между абсолютной отметкой точки наблюдения (Н) и приращением силы тяжести на этой высоте (Dg_с.в.) можно записать в виде:

Dg_с.в. = 0,3086·Н. (2.64)

Эта поправка называется поправкой за высоту точки стояния в свободном воздухе, или редукцией Фая.

2. Поправка за плотность пород промежуточного слоя.

Поправка за высоту определяется из предположения, что между уровнем моря и поверхностью наблюдений ничего нет. На самом же деле в пространстве между уровнем моря и рельефом поверхности съемки находятся горные породы с плотностью σ_п.с. (так называемая плотность пород промежуточного слоя) (рис. 2.24).

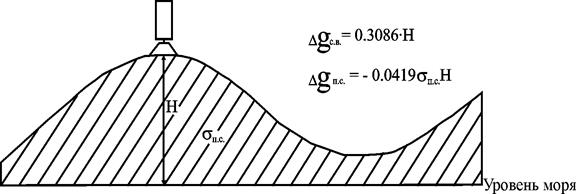
Рис. 2.24. Поправки за высоту точки стояния и плотность пород

промежуточного слоя

Поправка за плотность промежуточного слоя определяется, согласно теории, также из простого соотношения:

Dg_п.с. = - 0,0419σ_п.с.Н (2.65)

Минус в формуле поставлен из-за того, что породы плотностью σ_п.с. завышают значение силы тяжести, поэтому поправка всегда отрицательна. В практике обработки обычно обе эти поправки объединяются в одну и суммарная поправка называется поправкой (или редукцией ) Буге:

Dg_б = Dg_с.в. + Dg_п.с. = (0,3086 – 0,0419σ_п.с.) Н (2.66)

Кроме того, для целей разведочной геофизики необходимо знать аномальное поле, а его невозможно вычислить, не зная нормального поля. Как известно, фигуру Земли определяет геоид – геометрически сложная поверхность равных значений потенциала силы тяжести, совпадающая с невозмущенной поверхностью мирового океана и продолженная под континентами. Из теории гравитационного потенциала следует, что геоид очень близок к сфероиду с малым сжатием. Поле силы тяжести на поверхности сфероида или трехосного эллипсоида определяется из теоремы Клеро:

g₀= g_э(1 + b·sin²j - b₁·sin²2j), (2.67)

где j - географическая широта точки, g_э – значение силы тяжести на экваторе. Для определения коэффициентов b и b₁ следует измерять значения силы тяжести в большом числе точек, равномерно распределенных на земной поверхности. Таким образом можно составить столько уравнений типа (2.67), сколько сделано наблюдений. В правые части уравнений подставляют координаты j точек наблюдений, в левые – значения g₀, полученные из наблюдений и редуцированные к уровню моря. Затем, если полученную систему уравнений решить по способу наименьших квадратов, можно получить уравнение (2.67) в численном виде. Имеется множество формул нормального распределения силы тяжести, выведенных различными авторами. Для нашей страны наилучшим образом представляет Землю эллипсоид О.Н. Красовского, имеющий сжатие 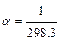. Эллипсоиду О.Н. Красовского наиболее соответствует формула нормального поля, полученная Гельмертом (1901–1909гг.):

g₀ = 978030 (1+0,005302 sin²j - 0,000007 sin²2j) – 14 (мгл). (2.68)

Аномальное значение (g_а) вычисляется как разность наблюденного значения силы тяжести в редукции Буге и значения нормального поля (g₀) в каждой точке наблюдения:

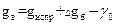, (2.69)

где Dg_б определяется по формуле (2.66).

Согласно инструкции по гравиразведке, при проведении гравиразведочных работ необходимо вычислять редукцию Буге с тремя плотностями:

s₁ = 2,67 г/см³ (средняя плотность верхней части земной коры);

s₂ = 2,3 г/см³ (средняя плотность осадочного слоя)

и s₃ – реальная средняя плотность пород района.

Значение g_а, вычисленное по формуле (2.69), называют аномальным значением силы тяжести в неполной топографической редукции, так как здесь ещё не учтено гравитационное влияние окружающего рельефа.