Пример расчета коэффициента корреляции Пирсона.

Допустим, что в результате лечения 12 больных с артериальной гипертензией в результате суточного мониторирования систолического артериального давления (САД) до лечения и после месячного лечения были получены следующие результаты:

№	САД до ( 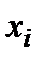)	САД после ( )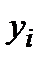
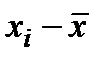
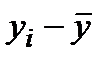
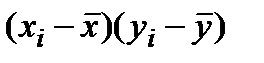
			-9,6	-7,5
			-19,6	-17,5
			-14,6	-12,5	182,5
			-4,6	7,5	-34,5
			0,4	12,5
			5,4	12,5	67,5
			-9,6	-7,5
			10,4	7,5
			15,4	12,5	192,5
			0,4	-7,5	-3
			5,4	-2,5	-13,5
			20,4	2,5

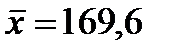
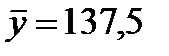
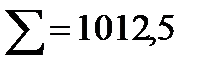
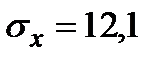
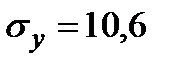
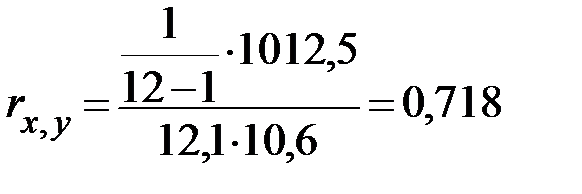
Итак, коэффициент корреляции получился равным 0,718.

Определим, достоверно ли он отличается от нуля. Для этого используем Таблицу 10 приложения. У нас 12 пар измерений, поэтому входим в Таблицу по 12 строке. На пересечении 12 строки и столбца Р=0,05 стоит число 0,576. Полученный коэффициент корреляции (0,718) больше этого числа. Следовательно, на этом уровне коэффициент корреляции достоверно отличается от нуля, то есть связь есть. На пересечении этой же строки и столбца Р=0,01 стоит число 0,708. Поскольку коэффициент корреляции больше и этого числа, следовательно, мы можем говорить, что связь существует и на этом более значимом уровне. Итак, ответ на первый вопрос таков: существование связи высоко достоверно. Далее, поскольку получено положительное значение коэффициента корреляции, мы заключаем, что связь прямая. Используя Таблицу 2 данного раздела, мы приходим к заключению, что связь сильная.

Найдем коэффициент детерминации:

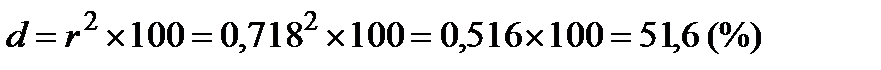
Таким образом, систолическое артериальное давление после лечения на 51,6 % определяется систолическим артериальным давлением до лечения, а на 48,4 % другими факторами.