ФУНКЦИОНАЛЬНАЯ, СТАТИСТИЧЕСКАЯ И КОРРЕЛЯЦИОННАЯ СВЯЗИ
Две случайные величины X и Y могут быть связаны функциональной зависимостью, статистической или быть независимыми. Как мы помним из курса математики, функциональной зависимостью называется такая зависимость, когда с помощью какого-либо закона (функции) заданному значению Х ставится в соответствие одно (или несколько) значений Y. Как отмечалось выше, точная функциональная зависимость в медицине практически не реализуется, так как обе величины X и Y или одна из них могут быть подвержены действию случайных факторов, в том числе и общих для них. В таком случае возникает статистическая связь.
Рассмотрим две случайные величины X и Y. Как мы уже знаем из предыдущего рассмотрения, для каждой из них существует свой закон распределения. Допустим далее, что Y зависит от X.
Статистической связью называется связь между величинами X и Y, при которой изменение одной из величин вызывает изменение закона РАСПРЕДЕЛЕНИЯ другой. Если мы имеем дело со случайными величинами, распределенными по нормальному закону, то это означает, что изменение Х может приводить к изменению или дисперсии или среднего (или того и другого) случайной величины Y. Рассмотрим ситуацию, когда изменяется среднее.
Хорошо известной является статистическая связь веса и роста. Выберем четырех людей одного роста, равного 165 см (то есть зададим х=165 см). Измерим их вес. Допустим, у нас получилось четыре значения: 62, 68, 59 и 65 килограмм. Найдем среднее арифметическое этих величин: 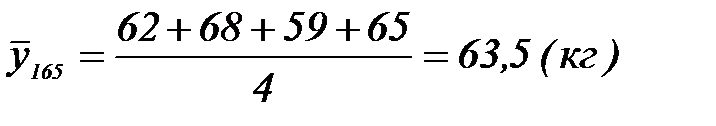
Число 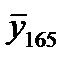 называется условным средним; черта над y есть обозначение среднего арифметического, а число 165 показывает, что рассматриваются те значения Y, которые соответствуют x=165 см. Таким образом, условным средним
называется условным средним; черта над y есть обозначение среднего арифметического, а число 165 показывает, что рассматриваются те значения Y, которые соответствуют x=165 см. Таким образом, условным средним 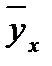 называется среднее арифметическое значений
называется среднее арифметическое значений 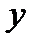 , соответствующих значению Х=х.
, соответствующих значению Х=х.
Если каждому значению х соответствует одно значение условной средней, то условная средняя есть функция х. В этом случае говорят, что случайная величина Y связана с Х корреляционно.
Итак, корреляционной зависимостьюY от Х называетсяфункциональная зависимостьусловной средней 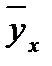 от х:
от х:
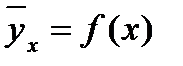 (1)
(1)
Дата добавления: 2016-06-05; просмотров: 2737;











