Элементы линейной алгебры

Системы линейных алгебраических уравнений.Дана система n линейных уравнений с n неизвестными:

a₁₁x₁+a₁₂x₂+…+a_1jx_j+…+a_1nx_n=b₁

a₂₁x₁+a₂₂x₂+…+a_2jx_j+…+a_2nx_n=b₂

…………………………………..

a_i1x₁+a_i2x₂+… +a_ijx_j+… +a_inx_n=b_i

…………………………………..

a_n1x₁+a_n2x₂+…+a_njx_j+…+a_nnx_n=b_n

В матричной форме эта система уравнений будет иметь вид:

,

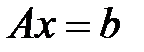где

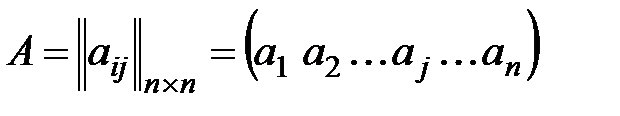- основная матрица системы уравнений размерности n на n;

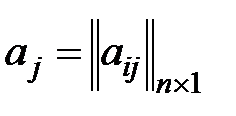- j-й вектор столбец основной матрицы системы уравнений;

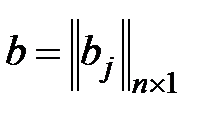- вектор столбец свободных членов системы уравнений;

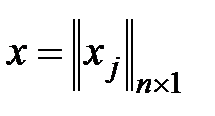- вектор столбец неизвестных системы уравнений;

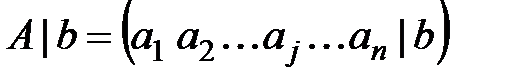- расширенная матрица системы уравнений.

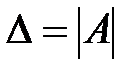- определитель основной матрицы системы уравнений;

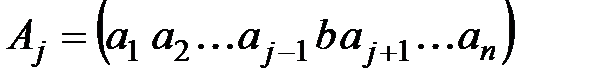- матрица, полученная из основной матрицы системы заменой j-го столбца (j-го вектора столбца 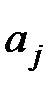) на вектор свободных членов ;

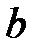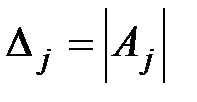- определитель матрицы, полученной из основной матрицы заменой j-го столбца (j-го вектора столбца 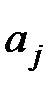) на вектор свободных членов .

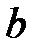Система линейных уравнений, имеющая хотя бы одно решение, называется совместной.

Система линейных уравнений, не имеющая ни одного решения, называется несовместной.

Система совместна и определена, если она имеет единственное решение.

Система совместна и не определена, если она имеет бесконечное множество решений.

Правило (теорема) Крамера. Если определитель основной матрицы системы уравнений 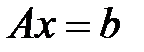отличен от нуля 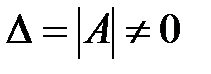, то система уравнений совместна и определена, т.е. она имеет единственное решение, определяемое для 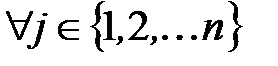как

.

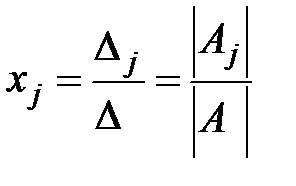Если определитель основной матрицы системы уравнений 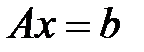равен нулю 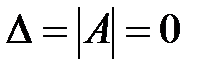и найдется хотя бы один определитель 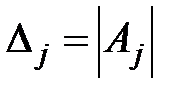отличный от нуля ( 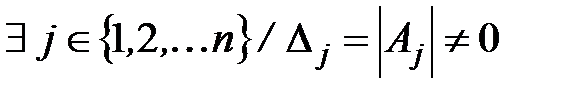), то система уравнений несовместна.

Если определитель основной матрицы системы уравнений 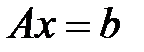равен нулю 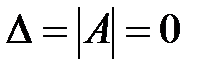и определители 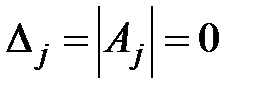для 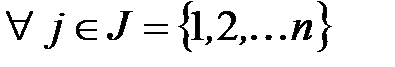), то система не определена и может иметь бесконечное множество решений или быть несовместной.

Свойства определителей.При расчете определителей необходимо учитывать следующие его свойства:

Свойство 1. Определитель не меняется при транспонировании матрицы.

Свойство 2. Если одна из строк (столбцов) состоит из нулей, то определитель равен нулю.

Свойство 3. Перестановка двух строк (столбцов) определителя изменяет его знак.

Свойство 4.Определитель, содержащий две одинаковые строки равен нулю.

Свойство 5. Если все элементы некоторой строки (столбца) определителя умножить на некоторое число k, то сам определитель умножится на число k.

Свойство 6. Определитель, содержащий две пропорциональные строки, равен нулю.

Свойство 7. Если все элементы i-й строки (столбца) определителя n-го порядка представлены в виде суммы двух слагаемых a_ij=b_j+c_j, то определитель равен сумме двух определителей, у которых все строки, кроме i-й, - такие же, как и в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов b_j, а в другом – из элементов c_j.

Свойство 8. Если одна из строк (столбцов) определителя равна линейной комбинации его других строк, то определитель равен нулю.

Свойство 9.Определитель не меняется, если к элементам одной из ее строк (столбцов) прибавляются соответственные элементы другой строки, умноженные на одно и то же число.

Свойство 10. Если все элементы определителя, расположенные по одну сторону от главной диагонали, равны нулю, то этот определитель равен произведению элементов, стоящих на главной диагонали.

Метод Жордана-Гаусса решения систем линейных алгебраических уравнений.Пусть имеется система линейных алгебраических уравнений:

A^.x=b

Если эту систему уравнений умножить слева на обратную матрицу:

A^{-1. A.} x=A^{-1 .} b,

то, учитывая, что A^-1А = Е - единичная матрица, получим:

x = A^-1. b

Таким образом, для того чтобы решить систему уравнений, необходимо одним из методов вычислить обратную матрицу и умножить ее на вектор правых частей системы.

Этот метод удобен в тех случаях, когда система уравнений решается при различных правых частях. Тогда необходимо один раз вычислить обратную матрицу, а затем, меняя правые части, вычислять произведение этой матрицы на столбец.

Алгоритм метода.

1. Выбирают первый слева столбец матрицы, в котором есть хоть одно отличное от нуля значение.

2. Если самое верхнее число в этом столбце ноль, то меняют всю первую строку матрицы с другой строкой матрицы, где в этой колонке нет нуля.

3. Все элементы первой строки делят на верхний элемент выбранного столбца.

4. Из оставшихся строк вычитают первую строку, умноженную на первый элемент соответствующей строки, с целью получить первым элементом каждой строки (кроме первой) ноль.

5. Далее проводят такую же процедуру с матрицей, получающейся из исходной матрицы после вычёркивания первой строки и первого столбца.

6. После повторения этой процедуры 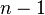раз получают верхнюю треугольную матрицу.

7. Вычитают из предпоследней строки последнюю строку, умноженную на соответствующий коэффициент, с тем, чтобы в предпоследней строке осталась только 1 на главной диагонали.

8. Повторяют предыдущий шаг для последующих строк. В итоге получают единичную матрицу и решение на месте свободного вектора (с ним необходимо проводить все те же преобразования).

Пример

Для решения следующей системы уравнений:

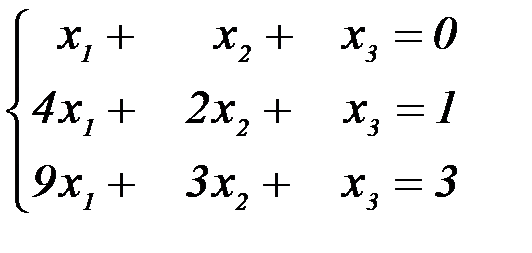
Запишем её в виде матрицы 3×4, где последний столбец является свободным членом:

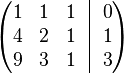
Проведём следующие действия:

· К строке 2 добавим: −4 × Строку 1.

· К строке 3 добавим: −9 × Строку 1.

Получим:

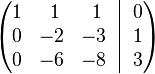
· К строке 3 добавим: −3 умноженную на Строку 2.

· Строку 2 делим на −2

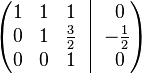
· К строке 1 добавим: −1 × Строку 3.

· К строке 2 добавим: −3/2 × Строку 3.

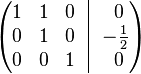
· К строке 1 добавим: −1 × Строку 2.

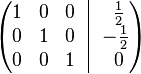
В правом столбце получаем решение:

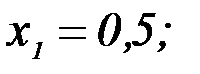
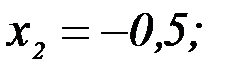
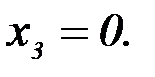
Методы решения задач линейного программирования.Существует довольно много типов задач линейного программирования и специфических методов их решения (рис. 2.2).

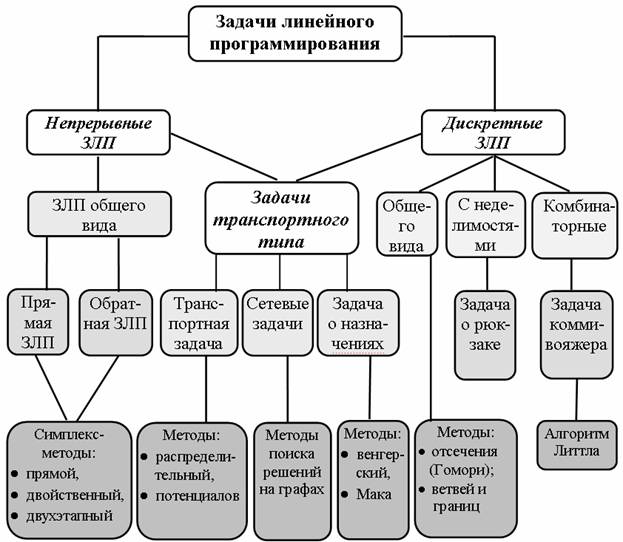
Рис.2.2. Задачи и методы линейного программирования

Все методы решения задач линейного программирования обычно разбиваются на две группы. Методы первой группы относят к конечным методам, то есть методам, обеспечивающим поиск оптимального решения задачи за конечное число шагов. Вторая группа – методы, реализующие итерационные процедуры поиска оптимума и приводящие к нахождению приближенного решения задачи. Конечные методы, в свою очередь, подразделяют на три основных класса:

1. Методы последовательного улучшения плана – симплексный метод решения задачи линейного программирования.

2. Методы последовательного уточнения оценок.

3. Методы последовательного сокращения невязок.

Методы последовательного улучшения плана по сути представляет собой применение метода Жордана-Гаусса к системе линейных алгебраических уравнений с количеством переменных большим количества уравнений. Такая система в общем случае имеет бесконечное множество решений, из которых с применением регулярной процедуры на каждом следующем шагенаходятся решения, улучшающие значение функционала задачи до тех пор, пока не будет достигнут оптимум.

Укрупненный алгоритм этого метода представлен на рис. 2.3.

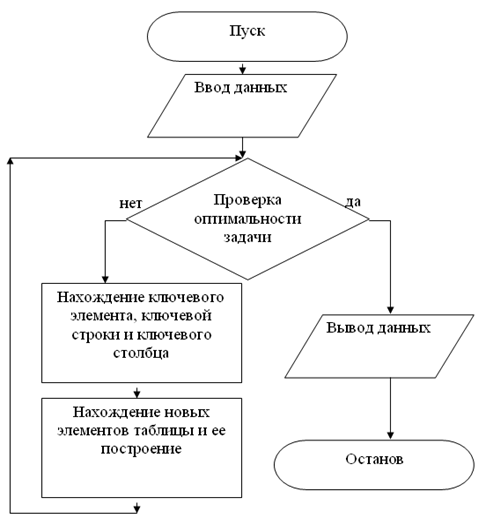
Рис. 2.3. Укрупненный алгоритм симплексного метода решения задачи ЛП

Глава 3. Планирование производства продукции на действующем промышленном предприятии