ВОЛНОВАЯ ОПТИКА. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

С точки зрения волновой оптики свет, или оптическое излучение, представляет собой совокупность поперечных монохроматических электромагнитных волн, распространяющихся в вакууме со скоростью света. Поперечность электромагнитной волны означает, что вектора напряженностей электрического и магнитного полей колеблются перпендикулярно направлению распространения волны, причем, как следует из уравнений Максвелла, векторы 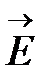, 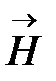и направление распространения волны образуют правовинтовую систему. Монохроматичность волны говорит о гармонической временной зависимости колебаний напряженности поля (то есть волна описывается тригонометрическими функциями – синусом или косинусом от частоты).

Простейшую математическую форму имеет плоская электромагнитная волна с линейной поляризацией (рис.1)

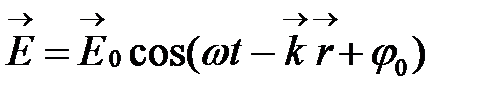
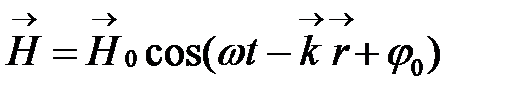(1)

где 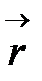– радиус-вектор точки пространства, в которой определяются поля; 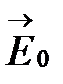и 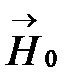– амплитуды колебаний электрического и магнитного полей; 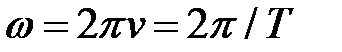= круговая (циклическая) частота, {\displaystyle f} 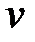– частота колебаний, Т– период колебаний; 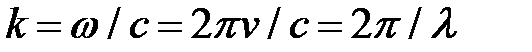– волновое число, 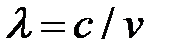– длина волны, 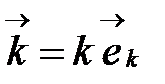– волновой вектор, 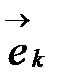– единичный вектор нормали к волновому фронту совпадающий с направлением скорости; с – скорость света. Аргумент периодической функции 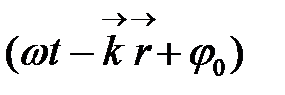называется фазой волны{\displaystyle T=1/f,}, 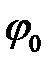– начальной фазой колебаний.

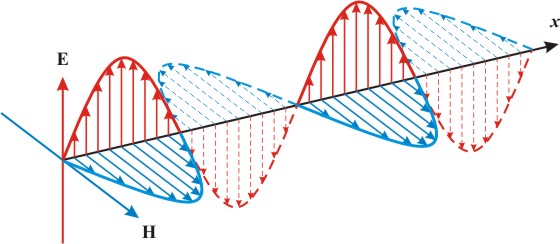
Рис. 1. Плоская линейно поляризованная электромагнитная волна

Определения.Волновой поверхностью называется геометрическое место точек, заданное уравнением 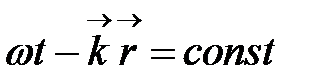, в которых колебания происходят в одинаковой фазе. По геометрии волновой поверхности различают плоские, сферические, цилиндрические, спиральные волны и др. Для плоской волны волновая поверхность является плоскостью, для сферической волны – сферой. Поверхность, до которой дошёл волновой процесс к данному моменту времени называется волновым фронтом. Различие между волновой поверхностью и волновым фронтом заключается в том, что в каждый момент времени существует лишь один волновой фронт и бесконечное (несчетное) количество волновых поверхностей. Нормаль к волновому фронту совпадает с направлением волнового вектора и направлением распространения волны в данной точке, а линия, касательная к которой в каждой точке совпадает с нормалью к волновым поверхностям, называется лучом волны. Плоской волне соответствует пучок параллельных прямых лучей, сферической волне – радиально расходящийся пучок лучей. Если на волновом фронте значения амплитуды волны одинаковы, то волна называется однородной. Примерами однородных волн являются плоские и сферические волны.

Уравнения Максвелла в вакууме и для небольших амплитуд колебаний электромагнитного поля в веществе, сравнимых, например, с напряженностью Е ~ 10³ В/м световых волн от Солнца на поверхности Земли, линейны. Это означает, что выполняется принцип суперпозиции: результирующий эффект процесса наложения друг на друга нескольких полей одной физической природы представляет собой алгебраическую сумму этих полей. То есть, есл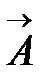и и 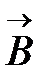являются решениями уравнений Максвелла, то решением будет и сумма 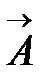+ 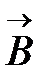. Не являясь законом природы, а свойством уравнений, этот принцип универсален, поэтому и «работает» не только в электростатике и магнитостатике, но и в оптике, акустике, и квантовой механике, т.е. во всех разделах физики, где используются линейные уравнения. А причина линейности уравнений Максвелла кроется в том, что при малых значениях напряженностей электромагнитных полей они не взаимодействует друг с другом. {\displaystyle {\vec {P}}}

Запишем уравнение плоской волны в экспоненциальной форме

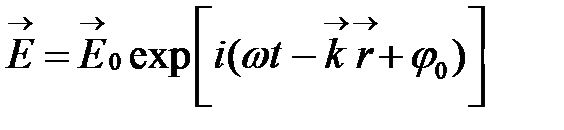
и, воспользовавшись принципом суперпозиции, найдем результирующее поле 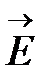, образованное наложением двух плоских монохроматических волн 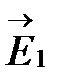и

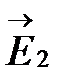
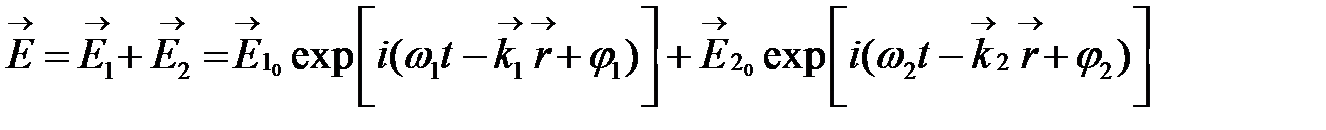(2)

Интенсивность суммарной волны 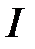равна квадрату амплитуды

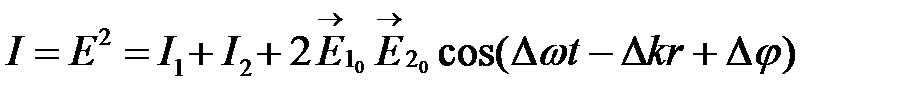(3)

{\displaystyle E^{2}=E_{1_{0}}^{2}+E_{2_{0}}^{2}+2{\mathbf {E} }_{1_{0}}{\mathbf {E} }_{2_{0}}\cdot \cos(\Delta \omega t+\Delta {\mathbf {kr} }+\Delta \varphi )}где 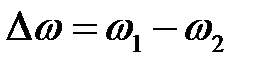{\displaystyle \mathbf {} \Delta \omega ={\omega }_{1}-{\omega }_{2}}, 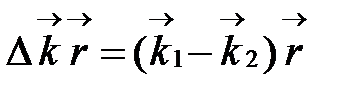, 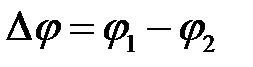{\displaystyle \Delta {\mathbf {kr} }={\mathbf {k} }_{1}{\mathbf {r} }_{1}-{\mathbf {k} }_{2}{\mathbf {r} }_{2}}.

{\displaystyle \Delta \varphi ={\varphi }_{1}-{\varphi }_{2}}

2. ИНТЕРФЕРЕНЦИЯ

Если 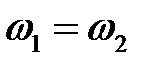, то разность частот 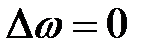, т.е. в уравнении (3) третье слагаемое становится стационарным, не зависящим от времени, а разность фаз 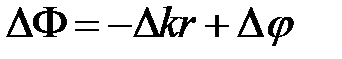– функцией только от точки пространства. Волны, у которых одинаковые частоты (длины волн), а разность фаз неизменна во всех точках области пространства, в которых происходит наложение волн, называются когерентными. В случае, когда в формуле (3) скалярное произведение 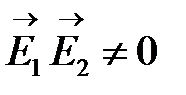, наложение когерентных волн приводит к перераспределению интенсивности, за которое отвечает третье слагаемое называемое интерференционным членом. Пространственное перераспределение интенсивности света в результате наложения (суперпозиции) нескольких когерентных световых волн называется интерференцией. В результате перераспределения интенсивности на экране или фотопленке возникает интерференционная картина из чередующихся светлых и темных полос. Интерференционные картины от двух когерентных точечных источников при увеличении расстояния между ними (по горизонтали) и увеличении частоты волны (по вертикали) изображены на рис. 2. Область пространства, в которой наблюдается интерференционная картина, называется полем интерференции.

Рис. 2. Интерференционные картины когерентных сферических волн от двух точечных источников

Есл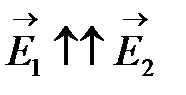и и 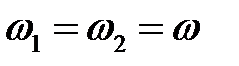, то из формулы (3) получаем хорошо известное соотношение для интенсивностей

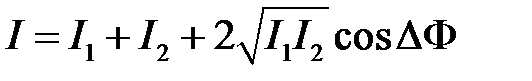(4)

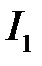где и 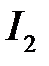– интенсивности интерферирующих волн, 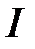– суммарная интенсивность. Так как значения косинуса изменяются в зависимости от фазы от 1 (DF = 0) до -1 (DF = p), то из формулы (4) следует, что при равенстве интенсивностей интерферирующих волн 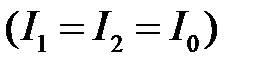и

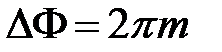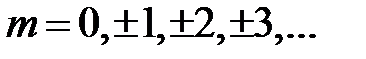, (5)

мы будем наблюдать интерференционные максимумы, в которых результирующая интенсивность будет 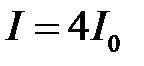, т.е. в четыре раза выше интенсивностей первоначальных волн, а при

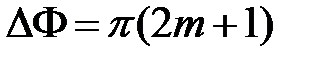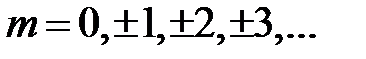, (6)

результатом наложения будет нулевая интенсивность I = 0, т.е. будут наблюдаться интерференционные минимумы.

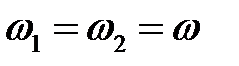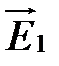
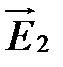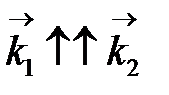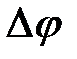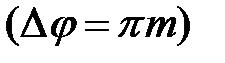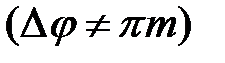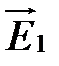
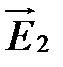
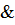
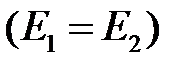
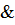
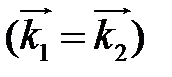
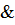
Если и , то есть плоскости поляризации волн перпендикулярны, принцип суперпозиции выполняется, но интерференционный член равен нулю и интерференция не возникает. Если при этом дополнительно выполняется условие , то, в зависимости от разности фаз образуется либо новая линейно поляризованная волна , либо эллиптически поляризованная волна . При выполнении условий 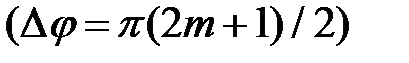, где & - конъюнкция, логическое «и», возникает волна с круговой (циркулярной) поляризацией.

Интерференция не наблюдается также и при суперпозиции падающей перпендикулярно зеркалу и отраженной волны ( 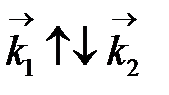), так как при этом образуется стоячая волна (рис. 3).

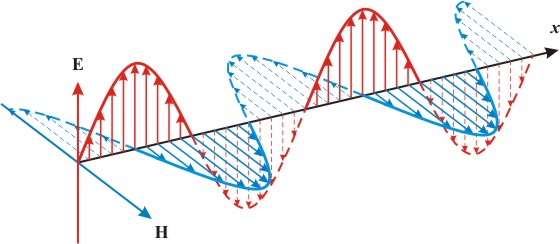
Рис. 3. Стоячая электромагнитная волна

Условия монохроматичности световых волн – их бесконечность и гармоничность – являются идеализацией. Отдельные атомы испускают свет за время Dt ~ 10^-9–10^-10 с и при более длительных временных интервалах когерентность излучения нарушается. Для описания процессов излучения конечной длительности вводят понятие волнового пакета, или цуга волн – «отрезка» квазимонохроматической волны конечной длины и шириной спектральной лини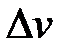и (или 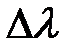). Мерой монохроматичности волнового пакета служит величина М = l/Dl. Длительность цуга 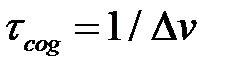{\displaystyle \tau _{coh}}называется временем когерентности, а длина 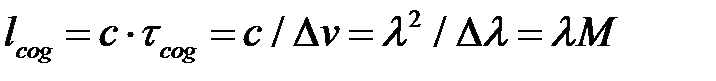{\displaystyle l_{coh}=c\tau _{coh}}– длиной когерентности, где {\displaystyle c}c – скорость распространения света, а l - средняя длина волны. Для квазимонохроматического света после пробегания одного гармонического цуга через выделенную точку пространства, он заменяется другим, примерно с той же частотой, но другой фазой. Это приводит к тому, что интерференционный член при наложении квазимонохроматических волн от разных источников хаотически осциллирует и его усредненное значение становится равным нулю, т.е. интерференции не возникает. Поэтому долгое время интерференцию в оптике удавалось наблюдать лишь в случае когерентных волн, получаемых путём либо деления волнового фронта (билинза Бийе, бипризма Френеля, зеркала Френеля, зеркало Ллойда, схема Юнга, дифракционные решетки и др.), либо делением амплитуды (тонкие плёнки, тонкие слои, полупрозрачные зеркала и др.). Только после появления лазеров стало возможным наблюдать интерференцию от независимых источников и в оптическом диапазоне, поскольку время их когерентности может достигать 10^-2 с и более.

2.1. Опыт юнга

Рассмотрим условия возникновения интерференционной картины, ее максимумов и минимумов в вакууме (показатель преломления n = 1) или воздухе (n » 1). Пусть на экран Э падают две когерентные волны 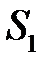и 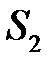, полученные делением излучения от одного источника S по схеме Юнга (рис.4), что позволяет исключить влияние начальной фазы 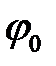. Источник волны S образован дифракцией плоской волны на экране с одним круглым отверстием.

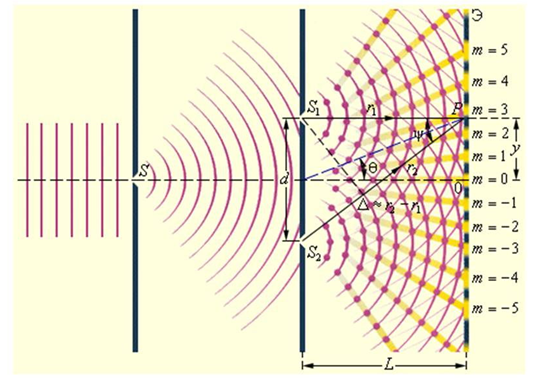
Рис. 4. Схема Юнга получения двух когерентных волн от одного источника

Допустим, один из полученных лучей прошел от источника излучения до определенной точки y на поверхности экрана путь 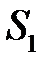, а второй – 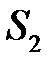(рис. 5).

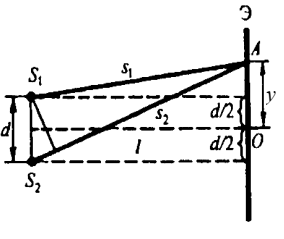
Рис. 5. Нахождение геометрической разности хода волн

Геометрическая разность хода волн равна

.

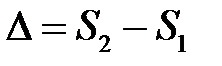Воспользовавшись теоремой Пифагора, выразим квадраты геометрических путей согласно рис. 5:

,

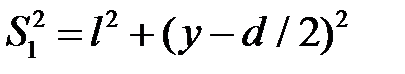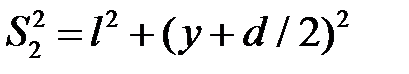(7)

Вычитая из второго уравнения первое и пренебрегая членом d²/4, получим:

.

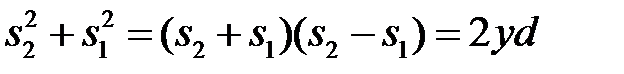Откуда:

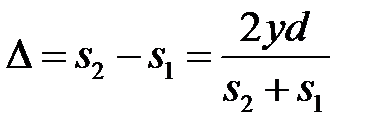(8)

Из условия следует 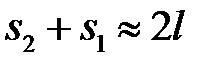, поэтому геометрическая разность хода в точке A равна

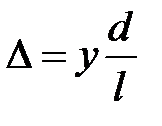(9)

Подставив выражение для разности хода (9) в условие наблюдения максимума (5) и минимума (6), получим выражение для расстояний от центра 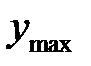и 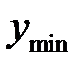для максимумов и минимумов интенсивности света:

положение максимумов при 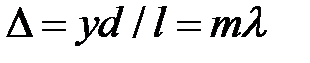отсюда:

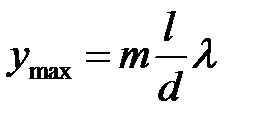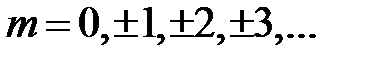, ( ) (10)

положение минимумов при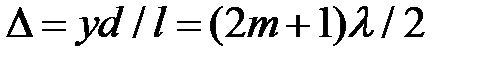

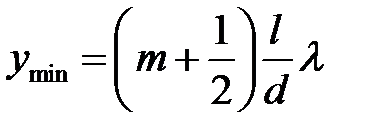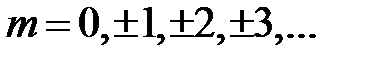, ( ) (11)

При распространении квазимонохроматических волн в среде с коэффициентом преломления 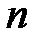скорость волн уменьшается в 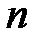раз по сравнению с вакуумом и на той же геометрической разности хода укладывается в 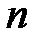раз больше длин волн l. Поэтому для нахождения условий максимума и минимума в среде вводится понятие оптической разности хода 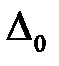, равной произведению геометрической разности хода на коэффициент преломления среды

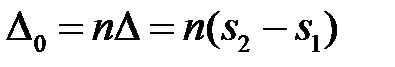
При расчетах оптической разности хода необходимо также учитывать сдвиг волны на половину ее длины при ее отражении от оптически более плотной среды, т.е. среды с бóльшим коэффициентом преломления:

.

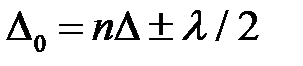2.2. Оптика тонких слоев

Оптика тонких слоев является разделом волновой оптики, в котором изучается прохождение света через один или несколько слоев непоглощающего вещества, толщина которых соизмерима с длиной световой волны. Специфика этого раздела заключается в том, что в ней главную роль играет интерференция света между частично отражаемыми на верхних и нижних границах слоев световыми волнами. В результате интерференции происходит усиление или ослабление проходящего или отражаемого света, причём эффект зависит от вносимой оптической толщиной слоев разности ходалучей, длины волны света, угла его падения и т. д. К эффектам оптики тонких слоев относятся полосы равного наклона, полосы равной толщины и кольца Ньютона.

2.2.1. Полосы равного наклона

Полосами равной толщины называются интерференционные полосы, наблюдаемые при освещении тонких оптически прозрачных слоев (плёнок) переменной толщины пучком параллельных лучей и обрисовывающие линии равной оптической толщины. Полосы равной толщины возникают, когда интерференционная картина локализована на самой плёнке, поэтому они видны невооруженным глазом, например, в случае интерференции в тонких плёнках. Полосами равного наклона называется интерференционная картина, возникающая при освещении плоскопараллельной пластины постоянной толщины рассеянным светом в результате интерференции лучей, отражённых от верхней и нижней её поверхностей и выходящих параллельно друг другу. Для наблюдения полос равного наклона надо собрать эти параллельные лучи на экране, находящемся в фокальной плоскости линзы.

Рассмотрим интерференцию в тонких пластинках. Пусть из воздуха ( 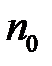= 1) на плоскопараллельную прозрачную пластинку с показателем преломления n и толщиной d от источника S под углом 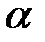падает плоская монохроматическая волна (рис. 6).

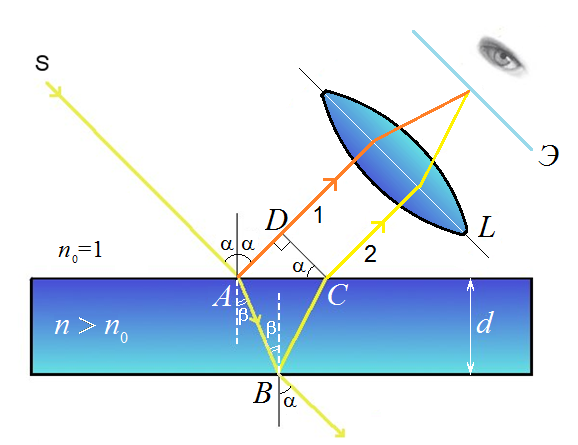
Рис. 6. Интерференция на плоскопараллельной пластинке: a – угол падения, b – угол преломления, луч 2 отстанет от луча 1, они сводятся линзой L на экране Э в один и интерферируют

В точке 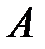луч частично отразится, а частично преломится под углом 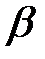, и, после отражения на нижней поверхности пластины в точке В, выйдет из пластины в точке С. Эффектами многократного отражения и преломления от внутренних поверхностей пластинки можно пренебречь из-за слабой интенсивности этих лучей.

Для наблюдения интерференционной картины лучи 1 и 2 собирают с помощью линзы L на экран Э или фотопластинку. Полученная интерференционная картина создается оптической разностью хода между параллельными когерентными лучами:

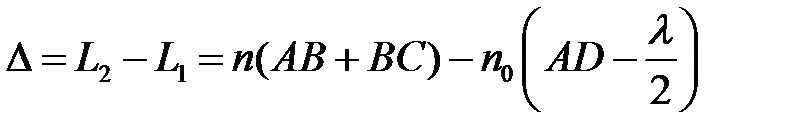(12)

В формуле учтено то, что при отражении света от более плотной среды ( 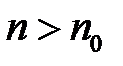) фаза изменяется на π, что равносильно потере полуволны. Из рисунка видно, что

,

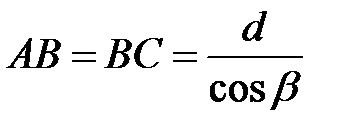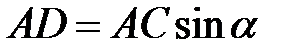
Учитывая закон преломления (закон Снеллиуса):

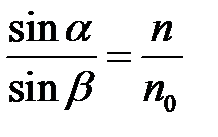
получим:

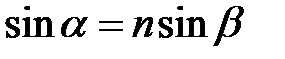
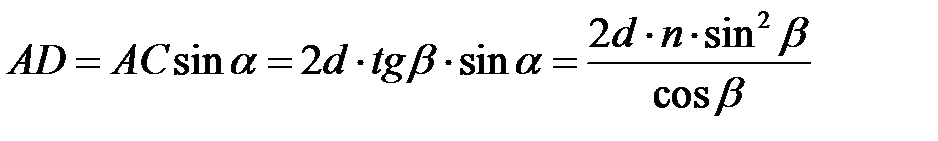
Подставляем полученные значения в {\displaystyle \ (1)}(12), получим оптическую разность хода

.

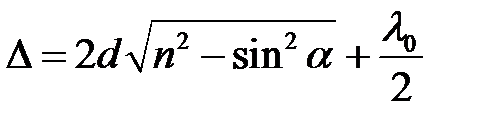Наложение двух лучей даст максимум, если 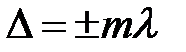и минимум, если 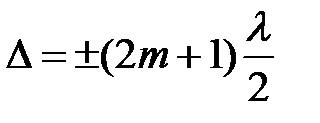. Таким образом, условие максимума интенсивности света при интерференции на плоскопараллельной пластинке запишется в виде

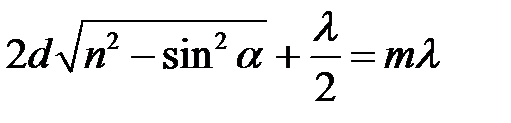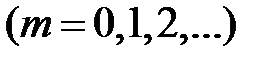, (13)

а условие минимума интенсивности света для полос равного наклона примет вид

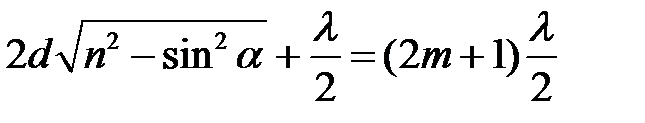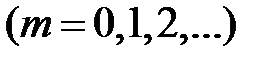, (14)

где m – порядок интерференции.

2.2.2. Полосы равной толщины. Кольца ньютона

Кольцами Ньютона называются интерференционные полосы равной толщины в форме колец, расположенных концентрически вокруг точки касания двух линз или линзы и стеклянной пластинки (рис. 7) и являются одним из случаев интерференции света на тонких пленках.

Кольца Ньютона наблюдаются и в проходящем, и – более отчётливо – в отражённом свете. При освещении монохроматической светом длины волны l кольца Ньютона представляют собой чередующиеся тёмные и светлые полосы (рис. 8). Светлые возникают в местах, где разность фаз между прямым и дважды отражённым лучом (в проходящем свете) или между лучами, отражёнными от обеих соприкасающихся поверхностей (в отражённом свете), равна 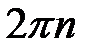(п = 1, 2, 3, ...) (т. е. оптическая разность хода D_m равна чётному числу полуволн).

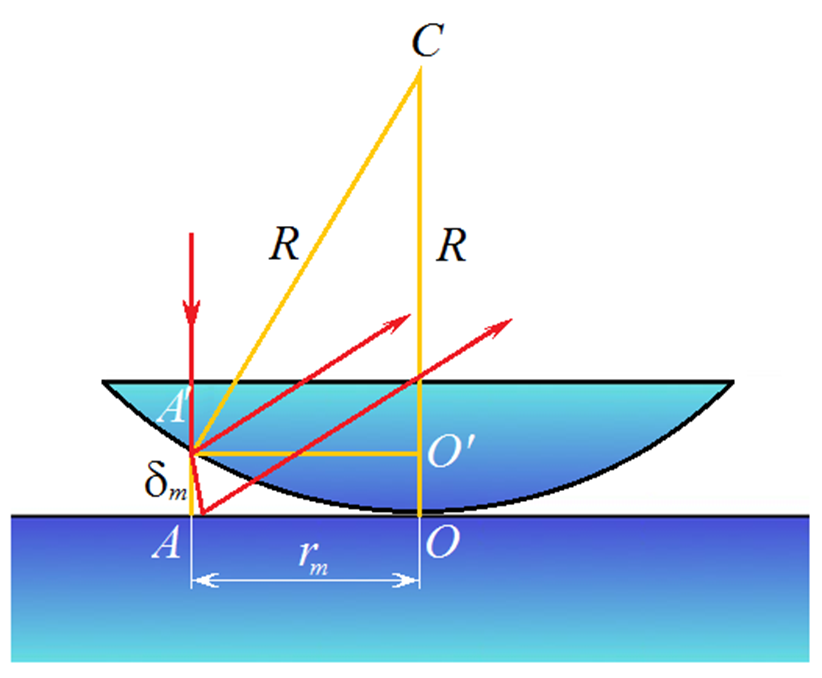
Рис. 7. Экспериментальная установка для наблюдения колец Ньютона в отраженном свете

Тёмные кольца образуются там, где разность фаз равна (2n + 1)p. Разность фаз лучей определяется толщиной зазора 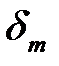с учётом изменения фазы световой волны при отражении. Так, при отражении от границы воздух - стекло фаза меняется на 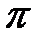, а при отражении от границы стекло - воздух фаза остаётся неизменной. Поэтому в случае двух стеклянных поверхностей (рис. 6), с учётом различий в условиях отражения от нижней и верхней поверхностей зазора (потеря полуволны), т-е тёмное кольцо образуется при толщине зазора 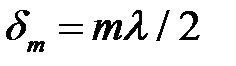, т.е. если

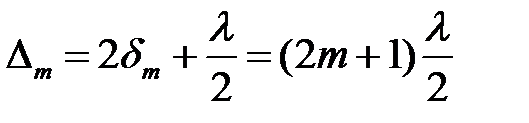
Радиус 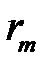т-го кольца определяется из треугольника А¢О¢С

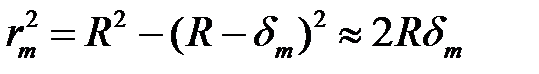
так как 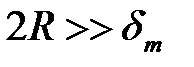. Откуда для тёмного m-го кольца

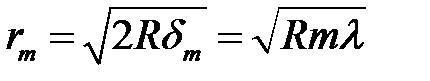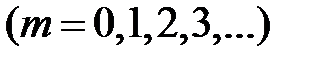, (15)

Аналогичный расчёт можно провести для светлых колец. Радиусы светлых колец:

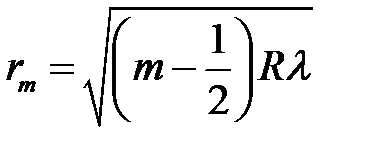(16)

Рис. 8. Кольца Ньютона

Эти соотношения позволяют с хорошей точностью определять 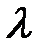по измерениям 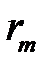. Если 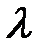известна, кольца Ньютона можно использовать для измерения радиусов кривизны линз и контроля правильности формы сферических и плоских поверхностей.

При практических расчетах определение радиуса кривизны линзы по одному измерению дает значительную погрешность из-за неточного определения радиуса колец (интерференционные кольца несколько размыты). Более точным является метод определения R по двум измерениям – для колец m и k порядков. Запишем формулу для m-го и k-го кольца:

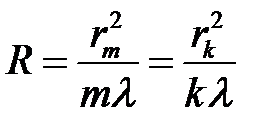
Решая эти уравнения, получим:

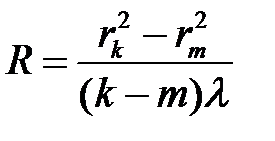
При выполнении опыта удобнее измерять диаметры D колец по шкале микроскопа, поэтому формулу необходимо привести к более удобному для расчета виду:

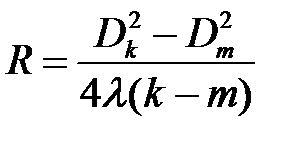(17)

При освещении белым светом кольца Ньютона становятся цветными.

III. ДИФРАКЦИЯ

Под дифракцией света в узком смысле понимается огибание световыми волнами контура непрозрачных тел, т.е. проникновение света в область геометрической тени; в широком смысле – проявление волновых свойств света в условиях, близких к условиям применимости геометрической оптики. Явление дифракции можно объяснить и рассчитать на основе принципа Гюйгенса-Френеля: каждая точка волнового фронта в определенный момент времени является источником вторичных сферических волн, огибающая которых становится фронтом исходной волны в следующий момент времени (Гюйгенс), причем амплитуда волны в любой точ­ке пространства является результатом интерференции когерентных вторичных волн (Френель). На рис. 9 изображено распространение фронтов плоской (а) и сферической (б) волны в оптически однородной среде и среде с непрерывно изменяющимся от точки к точке коэффициентом преломления (в), когда вторичные волны за одно и то же время проходят разные расстояния.

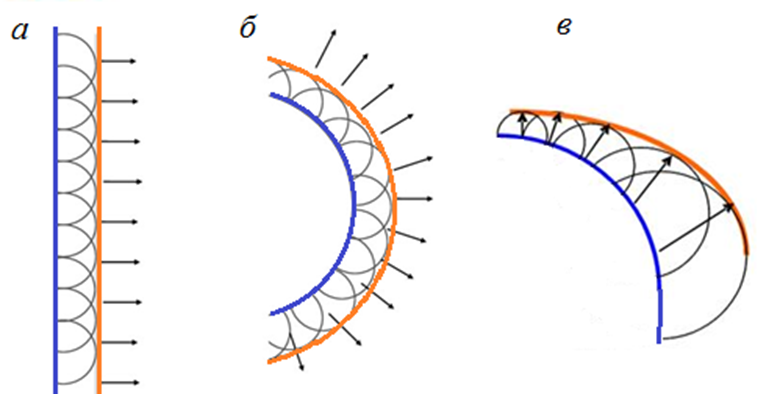
Рис. 9. Принцип Гюйгенса в случае распространения плоской (а) и сферической (б) волн в однородных средах и распространение волны в оптически неоднородной среде (в)

Г. Кирхгоф придал принципу Гюйгенса-Френеля строгий математический вид, представив вклад в амплитуду световой волны, который дает в точке Р излученная элементом dS поверхности волнового фронта вторичная волна в форме:

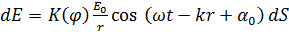(18)

где E₀ – амплитуда волны на поверхности волнового фронта, r – расстояние от элемента dS до точки Р на экране, j – угол между нормалью 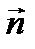к dS и 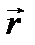, а коэффициент 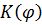монотонно изменяется от 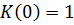до 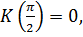не давая возможности вторичным волнам распространяться по направлению к источнику света (рис. 10).

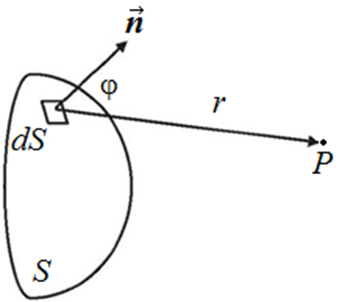
Рис. 10. К математической формулировке принцип Френеля-Гюйгенса

Различают два вида дифракции света. Дифракция вближней зоне (дифракционная картина образуется сходящимися лучами), носит название дифракции Френеля. Дифракция вдальней зоне (дифракционная картина образуется параллельными лучами) называется дифракцией Фраунгофера.

3. Дифракция

3.1. Дифракция френеля

На основе уточненного принципа Гюйгенса Френелем был разработан приближенный метод зон для расчета амплитуды колебаний электрического поля световой волны в некоторой точке пространства Р (рис. 11). Для наблюдения дифракции необходимо иметь источник света S, который будем считать точечным и монохроматическим, экран с круглым отверстием и экран для наблюдения. Размер отверстия определяет радиус 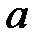сферической волновой поверхности.

По методу Френеля волновая поверхность разбивается на полуволновые зоны так, чтобы расстояния от границ соседних зон до точки наблюдения отличались одно от другой на половину длины волны 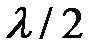(1, 2, ..., m - номера зон Френеля).

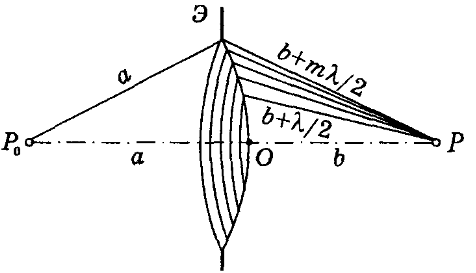
Рис. 11. Зоны Френеля

Квадрат радиуса m-ой зоны Френеля можно найти из теоремы Пифагора для левого треугольника (рис. 12):

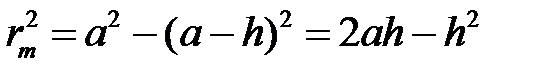
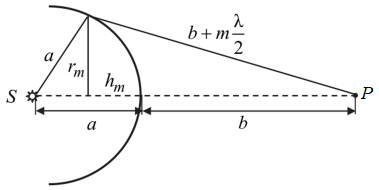
Рис. 12. Расчет радиуса m-ойзоны Френеля

С другой стороны, этот же радиус можно найти из геометрических соотношений для правого треугольника:

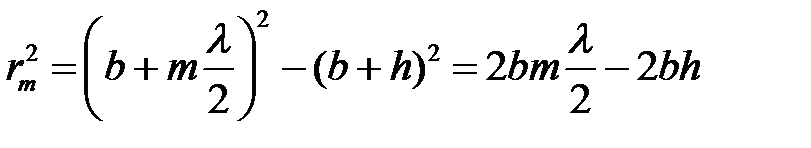
Так как и , при решении полученной системы уравнений можно пренебречь малыми членами 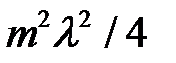и h². Выразим из первого уравнения h, подставим во второе и решим его относительно .

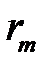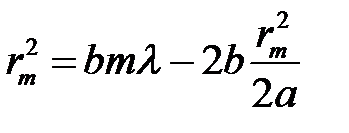
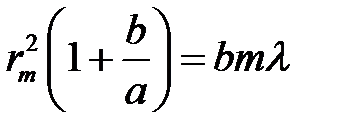
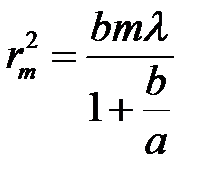(19)

Откуда получим выражение для радиуса m-ой зоны:

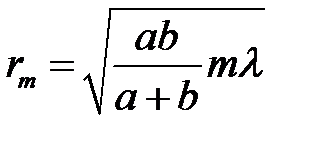(20)

Заметим, что, если падающая на данное отверстие волна является плоской ( 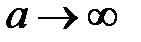), то радиус зоны рассчитывается по формуле

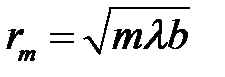
так как

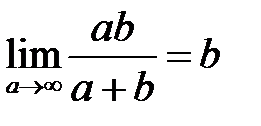
Из формулы (20) следует формула для числа полуволновых зон Френеля m

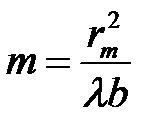
Таким образом, число полуволновых зон пропорционально квадрату радиуса отверстия ( 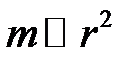) и обратно пропорционально расстояния от отверстия до экрана ( 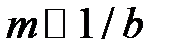). Это значит, что число зон увеличивается при увеличении радиуса отверстия, но уменьшается при увеличении расстояния от отверстия до экрана.

Сделаем оценку размера зон Френеля. При 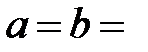10 см и 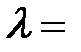500 нм радиус первой зоны 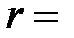0,158 мм. Следовательно, распространение света от S к Р происходит так, будто световой поток распространяется внутри очень узкого канала вдоль SР, т.е. прямолинейно. Таким образом, принцип Гюйгенса-Френеля позволяетобъяснить прямолинейное распространение света в однородной среде.

Волны от соседних зон приходят в точку Р в противофазе и осла­бляют друг друга. Поэтому результирующая амплитуда Е волны складывается (с учетом фаз) из амплитуд 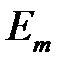волн, приходящих в данную точку из всех открытых зон Френеля:

.

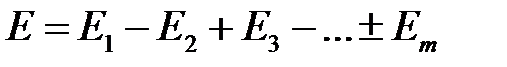Если на открытой части волновой поверхности укладывается неболь­шое нечетное число зон Френеля, то в точке Р будет наблюдаться све­тлое пятно (дифракционный максимум). Если на открытой части вол­новой поверхности укладывается четное число зон - в точке Р будет темное пятно (дифракционный минимум). Если увеличивать размер отверстия ( 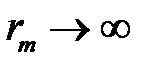r), то на волновой поверхности укладывается все большее число зон Френеля, а амплитуда в точке Р будет стремиться к половине амплитуды, созданной первой зоной, что легко показать, перегруппировав слагаемые знакопеременного ряда так, что он превратится в сумму положительных величин:

,

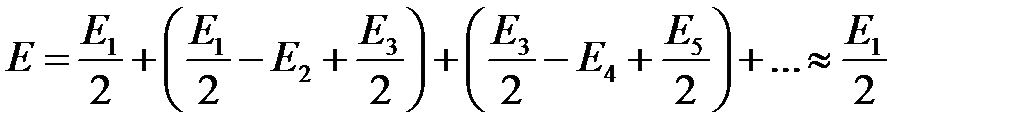так какусловие монотонного убывания амплитуд 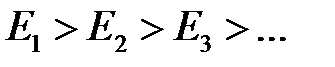приводит к тому, что все выражения в скобках практически равны нулю.

В случае дифракции Френеля на непрозрачном диске или шаре (рис. 13) в области геометрической тени возникает светлое пятно Пуассона (рис. 14), так как половина вклада в амплитуду первой открытой m-ой зоны Френеля не компенсируется вкладами остальных зон

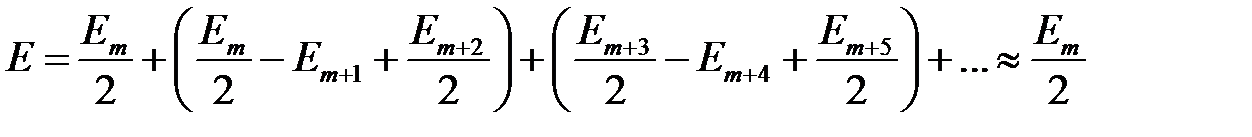
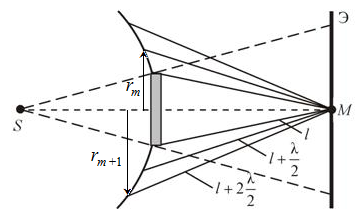
Рис. 13. Дифракция Френеля на непрозрачном диске

Существование этого пятна предсказал теоретически в 1818 году С.Д. Пуассон, пытаясь опровергнуть этим абсурдным, с точки зрения здравого смысла, теорию дифракции О. Френеля. Однако проведенный Д. Араго эксперимент подтвердил наличие этого пятна, что стало важным аргументом в пользу волновой теории света.

Рис.14. Фотография пятна Пуассона

Эффект появления пятна Пуассона противоположен рассмотренному выше эффекту возникновения темного пятна в центре освещенного круга при дифракции на отверстии при четном количестве открытых зон Френеля.

3.2. Дифракция фраунгофера плоской волны на щели

Рассмотрим дифракцию Фраунгофера, при которой дифракционная картина наблюдается на таком расстоянии от экрана со щелью, шириной b, что число открытых зон Френеля {\displaystyle F\ll 1} m <1. При этом условии падающая на щель волна является практически плоской. Кроме того, будем считать, что световая волна падает перпендикулярно на экран со щелью. Это означает, что волновая поверхность совпадает с плоскостью экрана. Параллельные диафрагируемые лучи из разных точек щели сводятся линзой на экран, расположенный в фокальной плоскости линзы. Так как световые лучи, собираемые линзой таутохронны, т.е. параллельные лучи, одновременно пересекающие перпендикулярную им плоскость затрачивают одинаковое время для достижения фокуса, то для расчета разности фаз от разных точек щели достаточно нахождения геометрической разности пути хода лучей, испущенных от центра щели 0 и точки 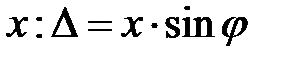, где 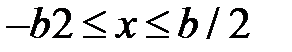(рис. 15):

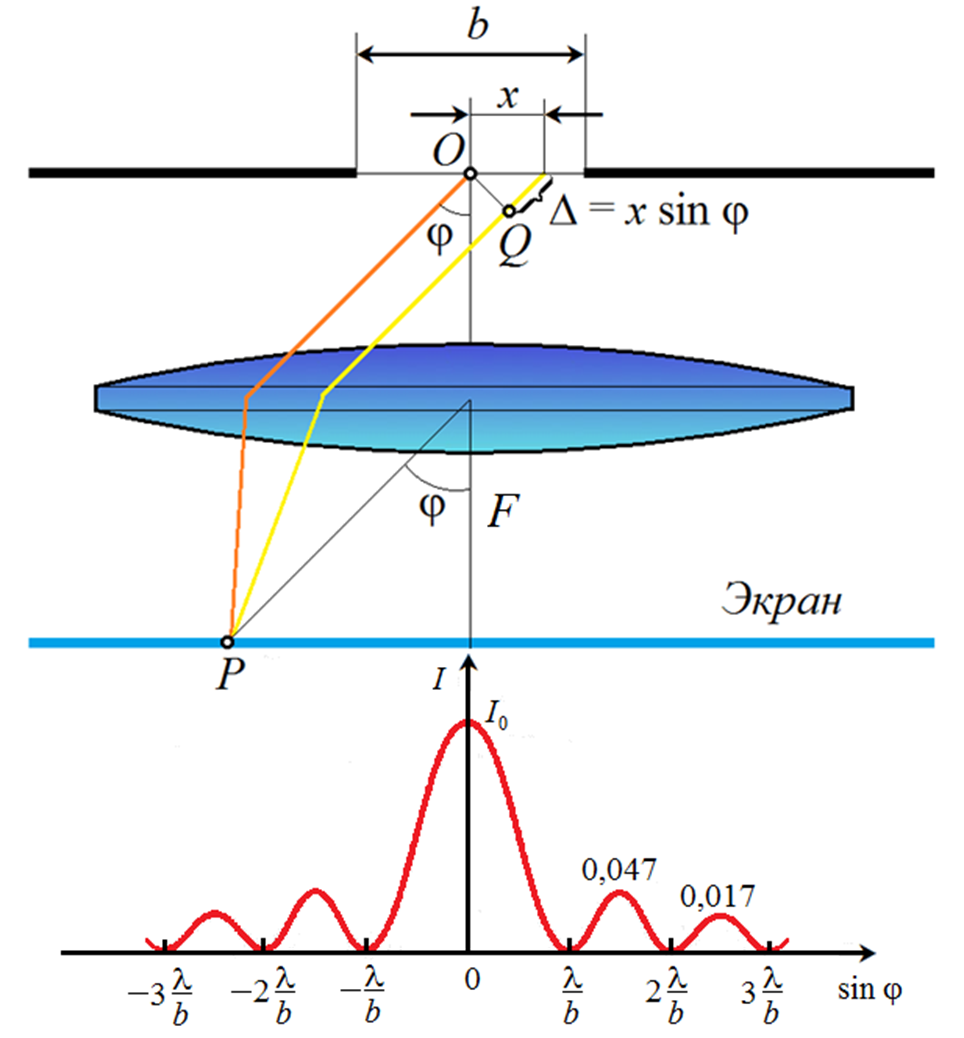
Рис. 15. Дифракция Фраунгофера на щели

Используя математическую форму принципа Гюйгенса-Френеля (18) и связь между амплитудой и интенсивностью 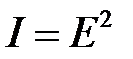легко получить формулу интенсивности света на экране в зависимости от угла j для дифракции Фраунгофера

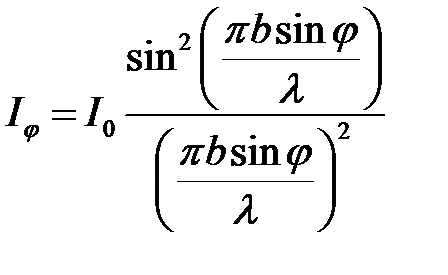(21)

При выполнении условия

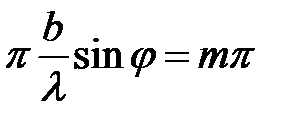
числитель формулы (21) обращается в ноль, из чего следует условие дифракционного минимума 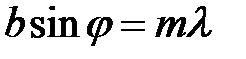. Наибольший максимум наблюдается, когда

,

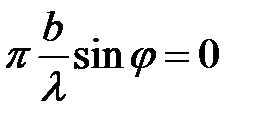т.е. когда 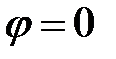, при этом 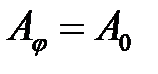. Другие условия максимумов являются решением трансцендентного уравнения

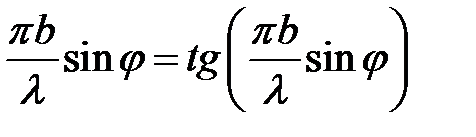
и определяются численными методами

,

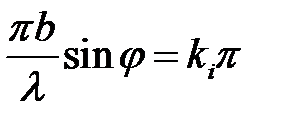где k₁ = 1,43, k₂ = 2,46, k₃ = 3,47, k₄ = 4,47 и т.д.

3.3. Дифракция на решетке

Дифракционной решёткой называется оптическое устройство, представляющее совокупность большого числа регулярно расположенных элементов, таких как щели, штрихи, канавки или выступы, на которых происходит дифракция света. По типу поверхности, на которую нанесены регулярные элементы различают плоские и вогнутые (сферические), прозрачные и отражательные, а в зависимости от того, на какую характеристику оптического излучения влияет решетка – амплитуду или фазу, различают амплитудные и фазовые дифракционные решетки. Простейшая пропускательная амплитудная дифракционная решетка, которая рассматривается в этом разделе, представляет собой ряд щелей на непрозрачном экране. Расстояние между центрами соседних щелей называют постоянной решетки d. В видимой области света применяют решетки, имеющие d от 0,5 мкм до 0,05 мм, в рентгеновской – от 16 мкм, а инфракрасной – до 4 мм.

Дифракционная картина, полученная с помощью такой дифракционной ре­шетки, определяется двумя факторами:

а) дифракцией света на отдельной щели;

б) интерференцией света от всех освещенных щелей.

Рассмотрим влияние первого фактора. При достаточно узких щелях решетки распределение главных максимумов на экране не зависит от количества щелей N и полностью определяется дифракцией Фраунгофера на одной из них по формуле (21). Однако малость углов j при работе с дифракционной решеткой вносит определенные коррективы в определение главных максимумов, поэтому нам потребуется простые дополнительные соображения.

Пусть плоская волна падает нормально на дифракционную решетку (рис. 16). Рассмотрим лучи, дифрагированные щелями решетки под некоторым угломj. Они попадут в определенную точку экрана, расположенного в фокальной плоскости линзы, так как линза собирает на ней все параллельные между собой лучи. Разность хода между лучами возникает на участке между решеткой и линзой, сама линза дополнительной разности хода не вносит. Разность хода между лучами, идущими из соседних щелей:

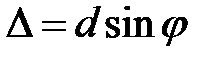(22)

Если на D укладывается целое число длин волн, то волны будут усиливать друг друга, и в точках экрана, где выполняется это условие, будут наблюдаться главные максимумы:

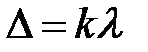(23)

Приравнивая формулы (22) и (23), получим условие главных дифракционных максимумов для решетки:

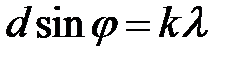(24)

где k = 0, 1, 2, ..порядок дифракционного максимума.

Из формулы (24) следует, что синус угла, под которым наблюдается дифракционный максимум, пропорционален l. Следовательно, при освещении дифракционной решетки белым светом наиболее сильно отклоняются длинноволновые красные лучи. При этом главный максимум нулевого порядка (k = 0 и 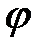= 0) не зависит от длины волны, то есть он представляет собой белое изображение источника, в то время как остальные максимумы будут окрашены от фиолетового на внутреннем крае спектра до красного цвета на внешнем. Спектры первого, второго и т.д. порядков располагаются симметрично по обе стороны от нулевого.

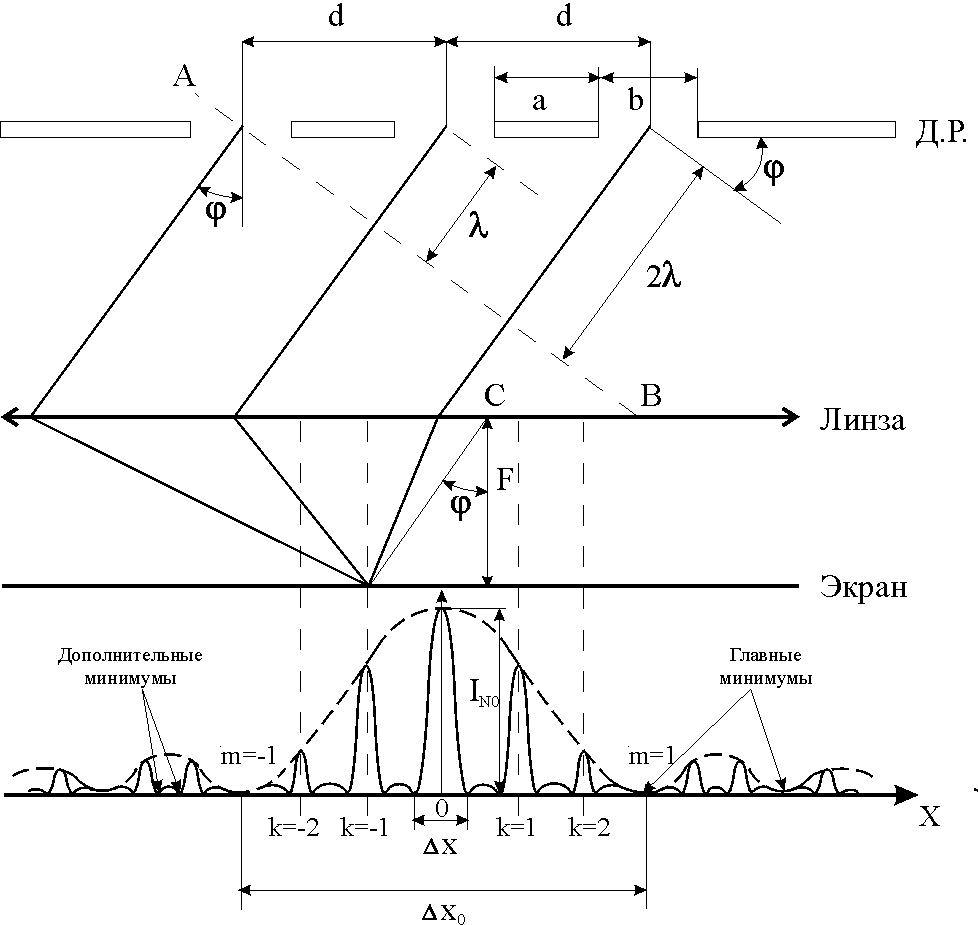
Рис. 16. Схема, иллюстрирующая принцип действия амплитудной щелевой дифракционной решётки

Условие главных дифракционных минимумов решетки соответствует условию минимума при дифракции света на щели, рассмотренной в предыдущем разделе

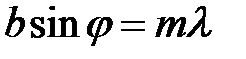(25)

Углы дифракции 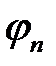, при которых наблюдаются максимумы интенсивности n-го и минимумы интенсивности k-го порядков находятся по формулам

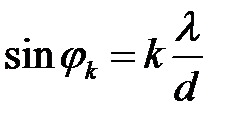
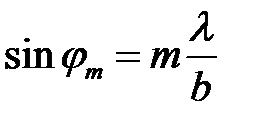(26)

где k, m = 0, ±1, ±2, ±3, … .

При малых углах дифракции координаты минимумов или максимумов на экране наблюдения можно найти из геометрических соображений по приближённой формуле: