Энергетическая светимость (интенсивность излучения)

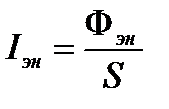, (35)

где 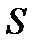– площадь поверхности, перпендикулярной к направлению распространения излучения, через которую переносится поток , т. е. представляет собой поверхностную плотность потока излучения. Единица энергетической светимости – ватт, делённый на метр в квадрате (Вт/м²).

Энергетическая сила света (сила излучения) 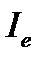определяется с помощью понятия о точечном источнике света – источнике, размерами которого можно пренебречь по сравнению с расстоянием до места наблюдения. Энергетическая сила света 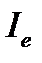– величина, равная отношению потока излучения источника к телесному углу ,в пределах которого это излучение распространяется:

. (36)

Единица энергетической силы света – ватт, делённыйна стерадиан (Вт/ср).

Энергетическая яркость (лучистость) 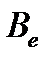– величина, равная отношению энергетической силы света 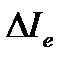элемента излучающей поверхности к площади 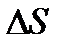проекции этого элемента на плоскость, перпендикулярную направлению наблюдения:

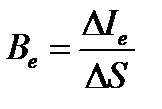. (37)

Единица энергетической яркости – ватт, делённый на стерадиан, умноженный на метр в квадрате (Вт/(ср·м²)).

Энергетическая освещённость (облученность). Энергетическая освещённость 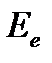, т. е. поверхностная плотность потока, падающая на данную поверхность, определяется по формуле

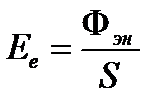. (38)

Энергетическая освещённость характеризует величину потока излучения, падающего на единицу освещаемой поверхности. Единица энергетической освещенности совпадает с единицей энергетической светимости (Вт/м²).

5.2. Световые величины

При оптических измерениях используются различные приемники излучения (например, глаз, фотоэлементы, фотоумножители), которые не обладают одинаковой чувствительностью к энергии различных длин волн, являясь, таким образом, селективными (избирательными). Каждый приемник излучения характеризуется своей кривой чувствительности к свету различных длин волн. Поэтому световые измерения, являясь субъективными, отличаются от объективных, энергетических, и для них вводятся световые единицы, используемые только для видимого света.

Основной световой единицей в СИ является единица силы света кандела(кд). Кандела есть сила света в заданном направлении источника, испускающего монохроматическое излучение частотой 540·10¹² Гц, энергетическая сила которого в этом направлении составляет 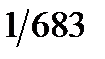Вт/ср (ватт, делённый на стерадиан).

Определение световых единиц аналогично энергетическим.

Световой поток 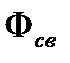определяется как мощность оптического излучения по вызываемому им световому ощущению (по его действию на селективный приемник света с заданной спектральной чувствительностью). Световым потоком , посылаемым источником света в некоторый телесный угол , называют величину, равную произведению силы источника света 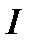на телесный угол, т. е.

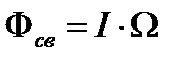. (39)

Единица светового потока – люмен (лм): 1 лм – световой поток, испускаемый точечным источником силой света в 1 кд внутри телесного угла в 1 ср. (при равномерности поля излучения внутри телесного угла) (1 лм = 1 кд∙ср).

Светимость 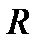определяется соотношением

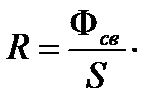(40)

Единица светимости – люмен, делённый на метр в квадрате (лм/м²).

Яркость 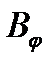светящейся поверхности в некотором направлении есть величина, равная отношению силы света в этом направлении к площади S проекции светящейся поверхности на плоскость, перпендикулярную данному направлению:

(41)

Единица яркости – кандела, делённая на метр в квадрате(кд/м²).

Освещенность Е – величина, равная отношению светового потока ,падающего на поверхность, к площади этой поверхности:

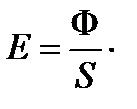(42)

Единица освещенности – люкс (лк): 1 лк – освещенность поверхности, на 1 м² которой падает световой поток в 1 лм (1 лм = 1 лм/м²).

Поток энергии Ф_эн, измеряемый в ваттах, и световой поток Ф_св, измеряемый в люменах, связаны соотношением

,

где А = 1,6 мВт/лм – константа, 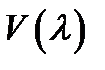– функция видности, определяемая чувствительностью человеческого глаза к излучению различных длин волн. Сила света (измеряется в канделах, кд)

, (43)

где 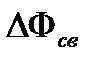– световой поток излучения, распространяющегося в малом телесном угле 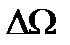. Освещенность(измеряется в люксах, лк):

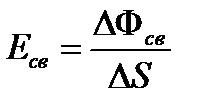, (44)

где – световой поток, падающий на малую поверхность площадью .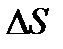

6. КВАНТОВАЯ ОПТИКА

Квантовой оптикой называется раздел оптики, описывающий явления, в которых проявляются квантовые свойства света: тепловое излучение, фотоэффект, эффект Комптона и т. п.

6.1. Тепловое излучение

Излучение, происходящее за счёт энергии теплового хаотического движения молекул вследствие нагревания тела, называется тепловым излучением. Тепловое излучение свойственно всем телам при температуре выше абсолютного нуля, имеет сплошной спектр, положение максимума которого зависит от температуры. При нагревании тела максимум излучения сдвигается с длинных инфракрасных волн в сторону более коротких – видимых и ультрафиолетовых, что проявляется при нагревании в видимой области как эффект изменения цвета тела от красного до фиолетового.

Тепловое излучение – единственный вид излучения, который может быть равновесным.

Количественной характеристикой теплового излучения служит спектральная плотность энергетической светимости (спектральная излучательная способность) тела – энергия, излучаемая за единицу времени с единицы площади поверхности тела в единичном интервале частот, измеряемая в Дж/м²:

,

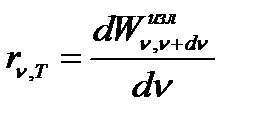где – энергия электромагнитного излучения, испускаемого за единицу времени (мощность излучения) с единицы площади поверхности тела в интервале частот от 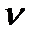до .

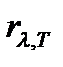Можно ввести аналогичную функцию длины волны , которая связана с формулой

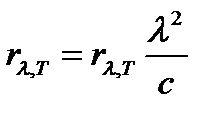
Здесь 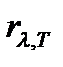– энергия, излучаемая за единицу времени с единицы площади поверхности тела в единичном интервале длин волн, измеряемая в Дж/(с м³).

Зная спектральную плотность энергетической светимости, можно вычислить энергетическую светимость (интегральную излучательную способность тела), просуммировав по всем возможным частотам:

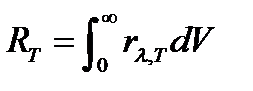
Способность тел поглощать падающее на них излучение характеризуется спектральной поглощательной способностью:

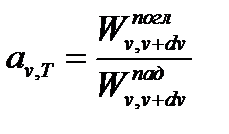
Спектральная поглощательная способность – величина безразмерная, она показывает, какая доля энергии, приносимой за единицу времени на единицу площади поверхности тела падающими на нее электромагнитными волнами с частотами от 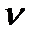до , поглощается телом. Величины 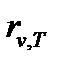и 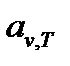зависят от природы тела, его термодинамической температуры и частоты излучения.

Тело, поглощающее все падающее на него излучение любой частоты, называется абсолютно черным телом (АЧТ). Его поглощательная способность всегда равна единице ( ). Такое тело является идеализацией. Абсолютно черных тел в природе нет, но есть тела, которые в определенном интервале частот имеют свойства, близкие к свойствам АЧТ (например, сажа, чёрный бархат, Солнце).

Моделью абсолютно черного тела является замкнутая оболочка с небольшим отверстием, внутренняя поверхность которой зачернена (рис. 38). Луч света, попавший внутрь такой полости, испытывает многократные отражения от стенок, в результате чего интенсивность вышедшего излучения оказывается практически равной нулю. Оболочка тем ближе по своим свойствам к свойствам АЧТ, чем меньше отношение площади отверстия к площади оболочки. Зрачок человеческого глаза, узкий вход в пещеру, окно здания и т. п. в некоторой степени приближаются по свойствам к такой оболочке, а значит к АЧТ.

Рис. 38. Модель абсолютно-чёрного тела

Тепловое излучение подчиняется законам Кирхгофа, Стефана-Больцмана и Вина.

Закон Кирхгофа: отношение спектральной плотности энергетической светимости тела к его спектральной поглощательной способности не зависит от природы тела, т. е. одинаково для всех тел, и для всех тел является универсальной функцией (функцией Кирхгофа) частоты (или длины волны) и температуры:

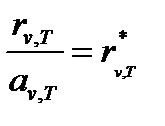(45)

Из закона Кирхгофа для АЧТ (с учётом, что 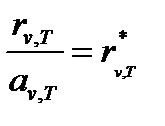) вытекает, что универсальная функция Кирхгофа 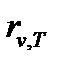есть не что иное, как спектральная плотность энергетической светимости абсолютно черного тела. Следовательно, согласно закону Кирхгофа, для всех тел отношение спектральной плотности энергетической светимости к спектральной поглощательной способности равно спектральной плотности энергетической светимости абсолютно черного тела при той же температуре и частоте. Cпектральная плотность энергетической светимости любого тела всегда меньше спектральной плотности энергетической светимости черного тела (при тех же значениях 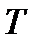и ).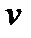

Зная поглощательную способность тела 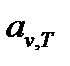и функцию Кирхгофа 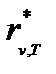, можно найти энергетическую светимость любого тела по формуле

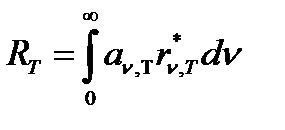. ( 46 )

Кроме АЧТ в физике теплового излучения существует понятие серого тела. По своим свойствам к серому телу близка Земля. Серое тело – это тело, поглощательная способность которого одинакова на всех частотах, следовательно, в последней формуле поглощательная способность может быть вынесена из-под знака интеграла, и энергетическая светимость серого тела может быть найдена по формуле

,

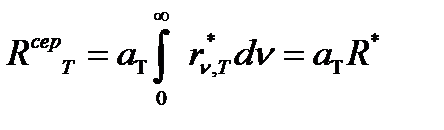где = 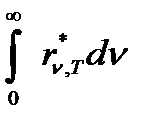– энергетическая светимость АЧТ.

Поиск вида функции Кирхгофа стал основной задачей теории теплового излучения. Но прежде, чем эта функция была установлена, был открыт закон Стефана-Больцмана, согласно которому энергетическая светимость абсолютно черного тела пропорциональна четвертой степени его термодинамической температуры:

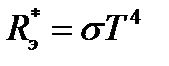(47)

где = 5,67 10^-8 Вт/(м² К⁴) – постоянная Стефана-Больцмана

Зависимость спектральной излучательной способности абсолютно чёрного тела 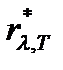от спектрального состава была установлена экспериментально и имела вид (рис. 39):

Рис. 39. Экспериментальные зависимости спектральной излучательной способности АЧТ от длины волны

На зависимости 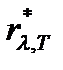есть максимум при определённой длине волны. Вин установил зависимость этой длины волны от температуры:

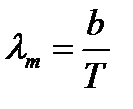, (48)

т. е. длина волны 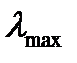, соответствующая максимальному значению спектральной плотности энергетической светимости 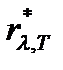черного тела, обратно пропорциональна его термодинамической температуре, b – постоянная Вина; ее экспериментальное значение равно 2,9 10^-3 м К. Этот закон (48) называют законом смещения Вина, поскольку он показывает смещение положения максимума функции 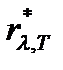по мере возрастания температуры в область коротких длин волн. Закон Вина объясняет, почему при понижении температуры нагретых тел в их спектре все сильнее преобладает длинноволновое излучение (например, переход белого каления в красное при остывании металла).

Правильное, согласующееся с опытными данными выражение для спектральной плотности энергетической светимости черного тела было найдено в 1900 г. немецким физиком М. Планком. Для этого ему пришлось отказаться от установившегося положения классической физики, согласно которому энергия любой системы может изменяться непрерывно, т. е. может принимать любые сколь угодно близкие значения. Согласно выдвинутой Планком квантовой гипотезе, атомы (квантовые осцилляторы) могут излучать энергию не в любом количестве, а определенными порциями – квантами, причем энергия кванта пропорциональна частоте осциллятора:

, (49)

где h=6,625 10^-34 Дж с – постоянная Планка.

Частица, уносящая такую энергию, называется фотоном, а энергия частицы – энергией фотона.

Планк вывел для универсальной функции Кирхгофа формулу

Или через частоту:

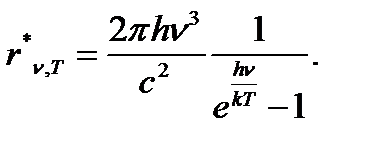(50)

Из этой формулы можно вывести закон Стефана-Больцмана, взяв интеграл (46), и можно вывести закон Вина, исследовав функцию 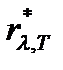на максимум.

Законы теплового излучения используются для измерения температуры раскаленных и очень удаленных самосветящихся тел (например, звезд). Совокупность методов таких измерений, использующих зависимость спектральной плотности энергетической светимости или интегральной энергетической светимости тел от температуры, называется оптической пирометрией. Приборы для измерения температуры нагретых тел по интенсивности их теплового излучения в оптическом диапазоне спектра называются пирометрами.

6.2. Фотоэффект

Различают фотоэффект внешний, внутренний и вентильный.

Внешним фотоэффектом называется выбивание электронов из вещества под действием света. Электроны, вылетающие из вещества при внешнем фотоэффекте, называются фотоэлектронами, а образуемый ими ток называется фототоком.

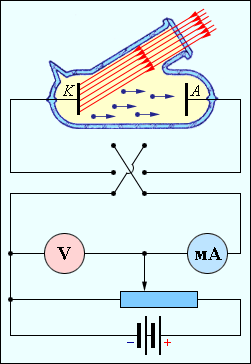
Рис. 40. Схема Столетова для наблюдения внешнего фотоэффекта

С помощью схемы Столетова (рис. 40) была получена следующая зависимость фототока от приложенного напряжения при неизменном световом потоке Ф (вольт-амперная характеристика (рис. 41)):

Рис. 41. Вольт-амперная характеристика фотоэффекта

При некотором напряжении фототок достигает насыщения 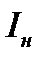. При этом все электроны, испускаемые катодом за секунду, достигают анода, следовательно, сила тока насыщения 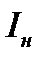определяется количеством электронов, испускаемых катодом в единицу времени под действием света. Число высвобождаемых фотоэлектронов пропорционально числу падающих на поверхность катода квантов света. А количество квантов света определяется световым потоком Ф, падающим на катод.

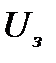– задерживающее напряжение – напряжение, при котором ни одному электрону не удается долететь до анода. Для этого случая можно записать закон сохранения энергии: энергия вылетающих электронов равна задерживающей энергии электрического поля (работе поля по торможению).

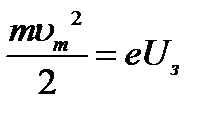. (51)

Отсюда, можно найти максимальную скорость вылетающих фотоэлектронов 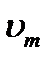по формуле

.

Первый закон внешнего фотоэффекта (закон Столетова): при фиксированной частоте падающего света фототок насыщения пропорционален падающему световому потоку:

.

Второй закон внешнего фотоэффекта: максимальная начальная скорость 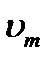фотоэлектронов не зависит от интенсивности падающего света Ф, а определяется только его частотой .

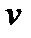Третий закон внешнего фотоэффекта: для каждого вещества существует «красная граница» фотоэффекта, то есть минимальная часто-та 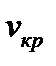, зависящая от химической природы вещества и состояния его поверхности, при которой ещё возможен внешний фотоэффект.

Второй и третий законы фотоэффекта нельзя объяснить с помощью волновой природы света (или классической электромагнитной теории света). Согласно этой теории, вырывание электронов проводимости из металла является результатом их «раскачивания» электромагнитным полем световой волны. При увеличении интенсивности светового потока (Ф) должна увеличиваться энергия, передаваемая электроном металла, следовательно, должна увеличиваться 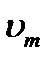, а это противоречит 2-му закону фотоэффекта.

Так как по волновой теории энергия, передаваемая электромагнитным полем, пропорциональна интенсивности светового потока (Ф), то свет любой частоты, но достаточно большой интенсивности должен был бы вырывать электроны из металла, то есть красной границы фотоэффекта не существовало бы, что противоречит 3-му закону фотоэффекта.

Внешний фотоэффект является безынерционным. А волновая теория не может объяснить его безынерционность.

В 1905 году А. Эйнштейн объяснил фотоэффект на основании квантовых представлений. Согласно Эйнштейну, свет не только испускается квантами в соответствии с гипотезой Планка, но и распространяется в пространстве и поглощается веществом в виде квантов. Уравнение Эйнштейна (закон сохранения энергии для внешнего фотоэффекта):

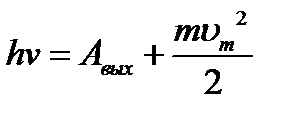. (52)

Энергия падающего фотона 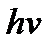расходуется на вырывание элек-трона из металла, то есть на работу выхода 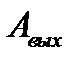, и на сообщение вы-летевшему фотоэлектрону кинетической энергии .

Наименьшая энергия, которую необходимо сообщить электрону для того, чтобы удалить его из твердого тела в вакуум, называется работой выхода. 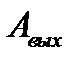зависит от рода вещества и температуры. Кроме того, работа выхода очень чувствительна к чистоте поверхности.

Уравнение Эйнштейна позволяет объяснить все три закона внешнего фотоэффекта.

1-й закон: каждый квант света поглощается только одним электроном. Поэтому число вырванных из вещества за время 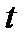фотоэлектронов должно быть пропорционально числу падающих на вещество в единицу времени фотонов, т. е. интенсивности светового потока Ф:

.

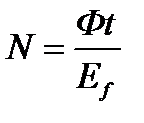2-й закон: максимальная скорость 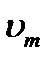вырванных светом фотоэлектронов зависит от частоты света , и т. к. работа выхода электронов из вещества 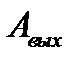не зависит от интенсивности светового потока Ф, то и максимальная скорость фотоэлектронов 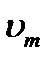не зависит от Ф:

.

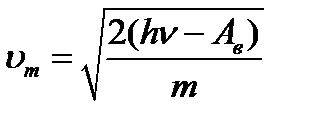3-й закон: при уменьшении частоты света ν уменьшается и максимальная скорость фотоэлектронов 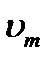, и при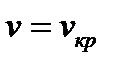 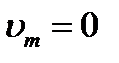. При этом 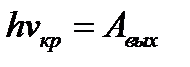, следовательно, . Т. е. существует минимальная частота, начиная с которой, фотоэффект прекращается.

На рис. 42 показана зависимость кинетической энергии фотоэлектронов от энергии падающих фотонов.

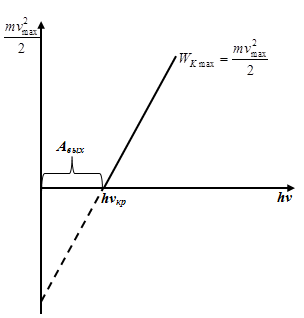
Рис. 42. Зависимость кинетической энергии фотоэлектронов от энергии падающих фотонов

Внутренний фотоэффект – это вызванные электромагнитным излучением переходы электронов внутри полупроводника или диэлектрика из связанных состояний в свободные без вылета наружу. В результате концентрация носителей тока внутри тела увеличивается, что приводит к возникновению фотопроводимости (повышению электропроводности полупроводника или диэлектрика при его освещении) или к возникновению ЭДС.

Вентильный фотоэффект, являющийся разновидностью внутреннего фотоэффекта – возникновение ЭДС (фото-ЭДС) при освещении контакта двух разных полупроводников или полупроводника и металла (при отсутствии внешнего электрического поля). Вентильный фотоэффект открывает, таким образом, пути для прямого преобразования солнечной энергии в электрическую.

На явлении фотоэффекта основано действие фотоэлектронных приборов, получивших разнообразное применение в различных областях науки и техники. В настоящее время практически невозможно указать отрасли производства, где бы не использовались фотоэлементы – приемники излучения, работающие на основе фотоэффекта и преобразующие энергию излучения в электрическую.

6.3. Свойства фотонов. Корпускулярно-волновой дуализм света

Согласно гипотезе о световых квантах Эйнштейна, свет испускается, поглощается и распространяется дискретными порциями (квантами), названными фотонами.

Энергия фотона

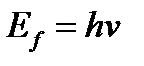(53)

Его масса 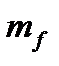находится из закона взаимосвязи массы и энергии:

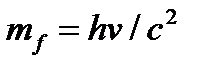(54)

Фотон – элементарная частица, которая всегда движется со скоростью света с = 3 10⁸ м/с и имеет массу покоя, равную нулю в отличие от электрона, протона и нейтрона, которые обладают отличной от нуля массой покоя и могут находиться в состоянии покоя.

Помимо энергии и массы, фотон обладает импульсом . В общей теории относительности получена связь между энергией и импульсом:

,

где – масса покоя, т. к. для фотона , то , следовательно,

.

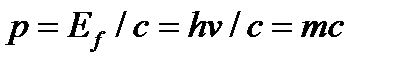Учитывая, что волновое число , , .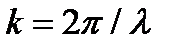

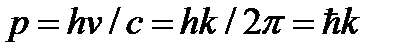Из сказанного выше следует, что фотон, как любая другая частица, обладает энергией, импульсом и массой и эти корпускулярные характеристики фотона связаны с волновой характеристикой света – частотой (длиной волны).

Более детальное рассмотрение оптических явлений приводит к выводу, что свойства непрерывности, характерные для электромагнитного поля световой волны, не следует противопоставлять свойствам дискретности, характерным для фотонов. Свет, обладая одновременно корпускулярными и волновыми свойствами, обнаруживает определенные закономерности в их проявлении. Так, волновые свойства света проявляются в закономерностях его распространения, интерференции, дифракции, поляризации, а корпускулярные – в процессах взаимодействия света с веществом. Чем больше длина волны, тем меньше энергия и импульс фотона и тем труднее обнаруживаются квантовые свойства света (с этим связано, например, существование красной границы фотоэффекта). Наоборот, чем меньше длина волны, тем больше энергия и импульс фотона и тем труднее обнаруживаются волновые свойства света (например, волновые свойства рентгеновского излучения (дифракция) обнаружены лишь после применения в качестве дифракционной решетки кристаллов).

6.4. Давление света

Экспериментальным доказательством наличия у фотона импульса является световое давление. Излучение, падающее на поверхность тела, оказывает на него давление. Электрическое поле световой волны напряжённостью 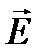приводит в упорядоченное движение элементарные заряды в веществе, а магнитное поле напряжённостью 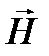действует на эти заряды с силой Лоренца (рис. 43).

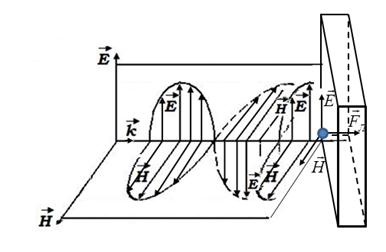
Рис. 43. Действие электрического и магнитного поля световой волны

на элементарные заряды вещества

Сила Лоренца оказывается направленной в сторону распространения излучения. Равнодействующая всех этих сил воспринимается как давление, оказываемое излучением на тело. Это объяснение давления с волновой точки зрения. С точки зрения квантовой теории давление света на поверхность обусловлено тем, что каждый фотон при соударении с поверхностью передает ей свой импульс.

Пусть свет падает по нормали к поверхности. Если в единицу времени (t = 1с) на единицу площади (S = 1м²) поверхности тела падает N фотонов, то при коэффициенте отражения ρ света от поверхности ( 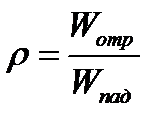) N фотонов отразится, а (1 – ρ) N – поглотится. Каждый фотон, поглощенный поверхностью, передаст ей импульс:

,

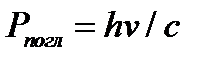а каждый отраженный:

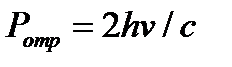
Давление света на поверхность равно импульсу, который передают поверхности в 1 с N фотонов:

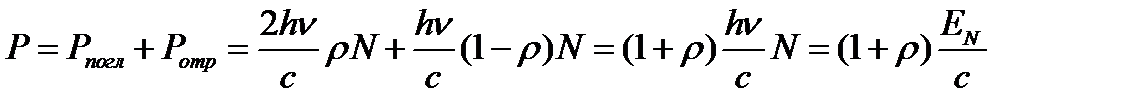
где – энергия всех фотонов, падающая на единицу поверхности в единицу времени.

Давление света, если свет падает под углом і,

.

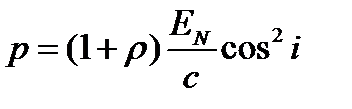6.5. Эффект Комптона

Эффект А. Комптона (1923 г.) является ещё одним эффектом, в котором проявляются корпускулярные свойства света (рис. 44). Эффект заключается в изменении длины волны рентгеновского излучения, рассеянного легкими атомами вещества (парафин, графит, бор).

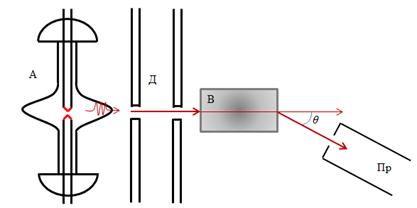
Рис. 44. Схема опыта Комптона

В опыте Комптона монохроматические рентгеновские лучи, создаваемые рентгеновской трубкой А, проходят через диафрагмы Д и узким пучком направляются на легкое рассеивающее вещество В. Лучи, рассеянные на угол 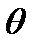, регистрируются приемником рентгеновских лучей 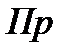– рентгеновским спектрографом, в котором измеряется длина волны рассеянных рентгеновских лучей. Опыты Комптона показали, что длина волны 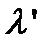рассеянного света больше длины волны 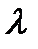падающего света, причем разность зависит только от угла рассеяния :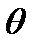

,

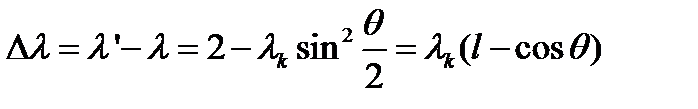где 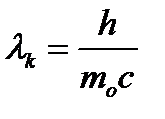= 2,43·10^-12 м – комптоновская длина волны электрона.

Объяснение эффекта Комптона дано на основе квантовых представлений о природе света. В легких атомах электроны слабо связаны с ядрами, поэтому электроны можно считать свободным. Тогда эффект Комптона – результат упругого столкновения рентгеновских фотонов со свободными электронами (рис. 45).

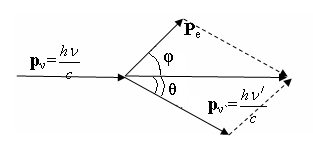
Рис. 45. Импульсы фотона ( 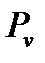и ) и 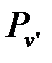электрона Рe при эффекте Комптона

Для упругого столкновения выполняется закон сохранения полной энергии и закон сохранения импульса. Будем до взаимодействия считать электрон покоящимся, после – релятивистским.

Закон сохранения энергии для эффекта Комптона (энергия системы до взаимодействия равняется энергия системы после взаимодействия):

,

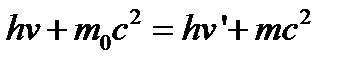где –энергия падающего фотона,

– энергия покоящегося электрона,

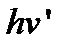– энергия рассеянного фотона,

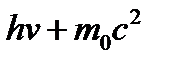– энергия системы фотон–электрон до взаимодействия.

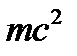– энергия движущегося электрона

Закон сохранения импульса для эффекта Комптона:

,

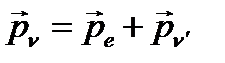или

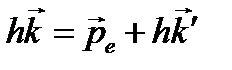
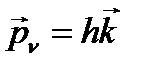– импульс падающего фотона;

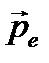– импульс электрона отдачи;

– импульс рассеянного фотона.

Решая совместно эти два уравнения, с учётом релятивистского соотношения между энергией и импульсом для электрона отдачи, получим окончательно

.

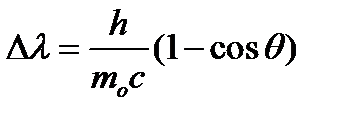7. Элементы квантовой механики и атомной физики

7.1. Модель атома Резерфорда

Э. Резерфорд в 1909 г. провел эксперименты по прохождению α-частиц сквозь тонкие металлические пластинки золота и платины (рис. 46). (α-частицы возникают при радиоактивных превращениях).

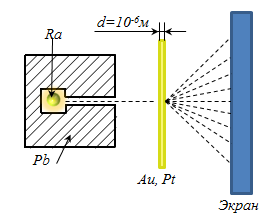
Рис. 46. Схема опыта Резерфорда

Заряд 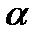-частицы равен двум зарядам электрона: = 2e = 2·1,6·10^-19 Кл, масса – четырем массам протона: 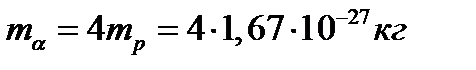. 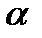-частицы испускались радием, помещенным внутри свинцовой полости с каналом так, чтобы все частицы, кроме движущихся вдоль канала, поглощались свинцом (рис. 46). Узкий пучок попадал на фольгу из золота перпендикулярно её поверхности. α-частицы, прошедшие сквозь фольгу и рассеянные ею, вызывали вспышки (сцинтилляции) на флуоресцирующем экране.

Опыты показали, что в большинстве случаев α-частицы после прохождения через фольгу сохраняли прежнее направление или отклонялись на очень малые углы. Однако некоторые 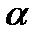-частицы (приблизительно одна из 20 000) отклонялись на большие углы, порядка 135 ÷ 150°. Т. к. электроны не могут существенно изменять движение 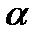-частицы, то Э. Резерфорд предположил, что весь положительный заряд атома сосредоточен в его ядре – области, занимающей весьма малый объём по сравнению со всем объёмом атома. Остальная часть атома представляет собой облако отрицательно заряженных электронов, полный заряд которых равен положительному заряду ядра. Эта модель атома была предложена Резерфордом в 1911 г. и получила название планетарной модели атома, т. к. она напоминает солнечную систему: в центре системы находится «солнце» – ядро, а вокруг него по орбитам движутся «планеты» – электроны (рис. 47).

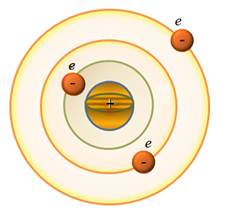
Рис.47. Модель атома Резерфорда

Противоречия модели Э. Резерфорда с наблюдаемыми фактами:

1. Электроны в планетарной модели не могут быть неподвижными, т. к. под действием силы Кулона они бы притянулись и «упали бы» на ядро. Уравнение движения электрона:

.

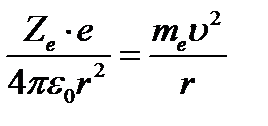В этой модели существует бесконечно много значений радиусов орбит электрона и соответствующих им значений скорости. Откуда следует, что радиус и скорость могут изменяться непрерывно, т. е. может испускаться любая порция энергии, и, следовательно, спектр атома должен быть сплошным. В действительности же опыт показывает, что атомы имеют линейчатые спектры.

2. При r ≈10^-10 м, ≈ 10⁶ м/с нормальное ускорение

.

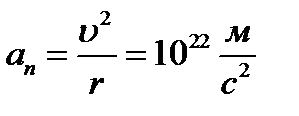Согласно электродинамике, электроны, движущиеся с ускорением, должны излучать электромагнитные волны и вследствие этого непрерывно терять энергию. И тогда электрон будет по спирали приближаться к ядру и через 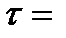10^-10 с должен упасть на него. С другой стороны, частота излучения должна непрерывно изменяться вследствие непрерывного изменения радиуса, частоты и периода обращения (r, ν, T). Следовательно, атом должен, опять же, давать непрерывный частотный спектр.

Попытки построить модель атома с использованием законов классической механики, электричества и оптики привели к противоречию с экспериментальными данными:

модель – а) неустойчивость атома; б) сплошной спектр;

эксперимент – а) атом устойчив; б) излучает при определенных условиях; в) линейчатый спектр.

Так светящиеся газы дают линейчатые спектры испускания, состоящие из отдельных спектральных линий. Спектр – совокупность частот гармонических составляющих или длин волн. Когда свет проходит через газы возникают линейчатые спектры поглощения – каждый атом поглощает те спектральные линии, которые сам может испускать.

Первым был изучен спектр самого простого элемента – атома водорода. Шведский учёный И. Ридберг установил, что длины волн известных в то время девяти линий спектра водорода могут быть вычислены по формуле

Эта формула называется формулой Бальмера – Ридберга.

= 10973731 м^-1 – постоянная Ридберга ( = 1,1·10⁷ м^-1).

Поскольку 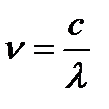, то можно записать:

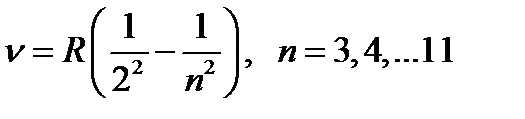(55)

где 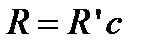= 3,29·10¹⁵ c^-1 – тоже постоянная Ридберга.

В настоящее время известно большое число спектральных линий водорода, длины волн которых с высокой степенью точности удовлетворяют формуле Бальмера – Ридберга (55). Из формулы Бальмера – Ридберга видно, что спектральные линии, отличающиеся различными значениями n, образуют группу или серию линий. С ростом n спектральные линии серии сближаются друг с другом.

В видимой части спектра расположена Серия Бальмера. Она была обнаружена первой.

В начале XX века в спектре атома водорода было обнаружено ещё несколько серий в невидимых частях спектра.

Таким образо