Средняя и мгновенная скорость. Среднее и мгновенное ускорения. Полное ускорение

Быстроту перемещения материальной точки в пространстве характеризует скорость.

Средней скоростью называется векторная величина, равная по модулю отношению перемещения ко времени, за которое это перемещение произошло:

.

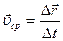Направление вектора 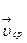совпадает с вектором перемещения .

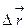Движение с постоянной скоростью ( 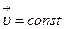)называют равномерным.

При неравномерном (переменным) движении быстроту движения тела характеризует мгновенная скорость.

Мгновенная скорость – величина численно равная производной перемещения по времени:

.

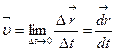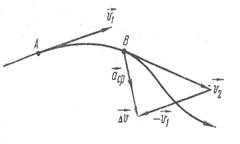
Вектор мгновенной скорости направлен по касательной к траектории движения (рис.4).

Быстроту изменения скорости со временем характеризует ускорение.

Средним ускорением называется векторная величина, равная отношению изменения скорости ко времени, за кото-

Рис. 4 рое это изменение произошло: .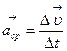

Вектор а_ср. направлен так же, как и вектор 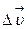(рис.5).

Движение с постоянным ускорением 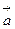называется равнопеременным.

При а > 0 - движение ускоренное, при а < 0 – замедленное.

Мгновенным ускорением называют предел:

,

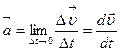т.е. ускорение – это производная скорости по времени.

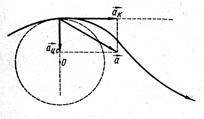
В ряде случаев ускорение удобнее представить в виде двух взаимно перпендикулярных составляющих, одна из которых отражает изменение скорости по величине (тангенциальная) 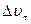вторая – по направлению (нормальная или центростреми-

Рис. 5тельная) : ,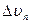

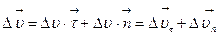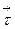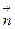где и - единичные векторы, направленные первый – по касательной; второй – перпендикулярно ей в каждой точке траектории.

Таким образом: ,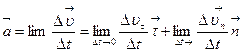

или с учетом обозначени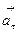й и 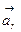запишем: .

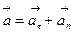В абсолютных значениях полное ускорение равно: .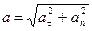

В свою очередь каждое из них определяется следующим образом:

; ,

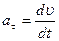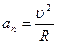где R - радиус искривления траектории.