Интерпретация полевых материалов МПП.

Решение обратной задачи МПП для полевых условий представляет значительную сложность ввиду того, что временная характеристика вторичного поля e(t_x) зависит не только от характеристик проводника, но и от взаимного расположения петли и проводника.

Ввиду этого особо важную роль играет моделирование. На сравнении результатов моделирования и полевых наблюдений и построена их интерпретация.

Тождественность результатов полевых измерений и моделирования вытекает из уравнений Максвелла при соблюдении критерия подобия:

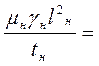
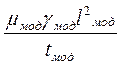. (151)

Рассмотрим результаты моделирования для наиболее простых проводников – шара, цилиндра, полупространства.

1. Вторичное поле проводящего шара зависит от радиуса шара,

его электропроводности g, радиуса петли R и расстояний между центрами петли и шара по вертикали Z и горизонтали Х. Зависимость эта выражается сложной формулой, содержащей полиномы Лежандра (рис. 43).

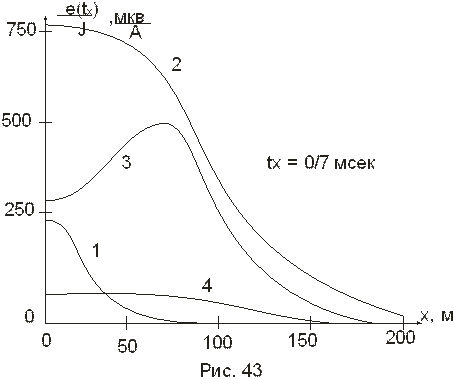
1 – R = 20 м, а = 30 м, Z = 50 м;

2 – R = 100 м, а = 50 м, Z = 30 м;

3 – R = 100 м, а = 20 м, Z = 70 м.

О геометрическом строении поля шара в какой-либо заданный момент времени t = 0.7 мсек, дают преставление графики вдоль эпицентральной линии. Если радиус шара а больше радиуса петли R, то ЭДС в заданный момент времени t_x имеет максимум только над центром тела при любой глубине его залегания (кривая 1). То же самое имеет место и при случае а/R < 1, но при достаточно больших Z (кривая 2). Небольшой шар на малой глубине, когда а/R < ¼ и а/Z ³ 2, дает 2 максимума, соответствующих прохождению провода петли непосредственно над телом (кривая 3). С увеличением глубины залегания тела эти максимумы исчезают и кривая принимает форму графика 4 с одинаковым значением ЭДС в центральной части аномалии. Ширина аномалии увеличивается с увеличением размеров шара и петли. По зависимости от х можно установить величину Z по формуле: Z = x₀ – R (где Z – глубина до центра шара, х₀ – координата при которой функция принимает значении 8% от ее значения в точке х = R (R – радиус петли).

2. Вторичное поле бесконечного цилиндра (рис. 44).

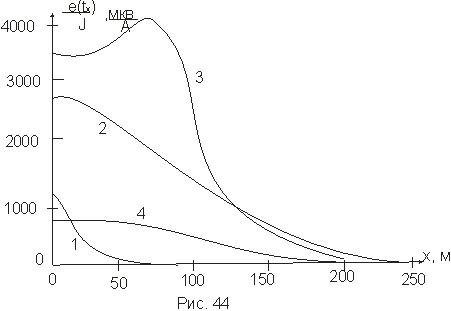
1 – R = 20 м, а = 20 м, Z = 30 м;

2 – R = 100 м, а = 50 м, Z = 80 м;

3 – R = 100 м, а = 20 м, Z = 30 м;

4 – R = 100 м, а = 20 м, Z = 70 м.

О распределении поля вдоль профиля (ось х) проходящего перпендикулярно оси цилиндра (ось у), можно судить по его кривым при t_x = 0.7 мсек. Основные закономерности распределения поля имеют те же характерные черты, что и для шара. При а/R << 1 кривая в точках х = R – а принимает максимальные значения. По сравнению с шаром эти максимумы менее выражены, что объясняется тем, что длина цилиндра превышает размеры петли. Глубина до центра цилиндра для большинства реальных соотношений a/R и Z/R определяется по той же эмпирической формуле, что и для шара.

Вторичное поле полубесконечной проводящей пластины (рис. 45).

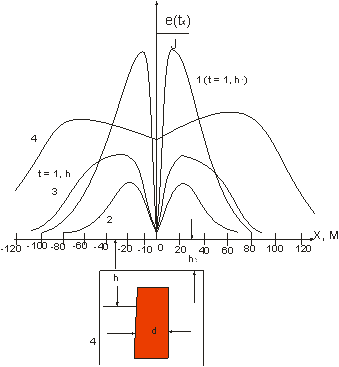
Рис. 45.

Величина зависит от g пластины, ее мощности и расположения относительно петли. Графики их более резко выражены, чем у шара и цилиндра и более сложны. Над тонкой вертикальной пластиной кривые = 0, по обе стороны от пластины – кривые симметричны, а прямо над пластиной – нули, независимо от глубины залегания h верхней кромки. Кривые 1 и 2 построены для разных времен (t = 1, 4). С увеличением h кривые выполаживаются и максимумы раздвигаются (кривая 3). При R << h расстояние между максимумами = 2h. С увеличением мощности пластины уже не равняется нулю над центром пластины (кривая 4).

При изменении угла падения пластины от 90⁰ до 0⁰ кривая становится все более ассиметричной. Максимум по падению тела резко возрастает, а со стороны лежачего бока убывает (рис. 46).

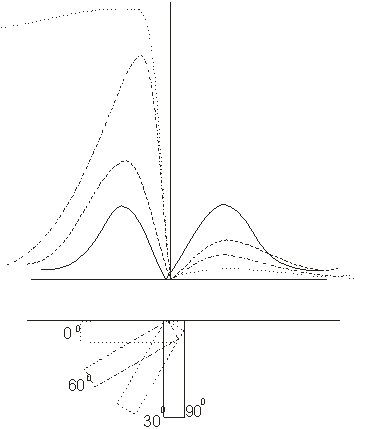
Рис. 46.

Зная формы графиков над различными телами, полученными в процессе моделирования можно приступать к интерпретации материалов полевых наблюдений.

По плану изолиний на разных временах t_x = 1 – 2 мсек, полученных при измерениях с петлей 200 х 200 м, можно оконтурить области с рыхлыми поверхностными отложениями повышенной проводимости. Воспользовавшись формулой
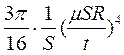= (152) можно определить продольную проводимость наносов S = d·g (где R – радиус петли). Если известна средняя электропроводность наносов g_ср в районах, то по S можно определить их мощность: d = S/g = Sρ.

С другой стороны, если известна мощность наносов, легко определить их удельное сопротивление.

По планам изолиний на поздних временах можно судить о протяженности и простиранию проводящего объекта. Если тело вытянуто, оно может быть аппроксимировано цилиндром или же пластиной. Для выяснения этого вопроса нужно использовать временные характеристики вдоль поперечных профилей. Если они практически не меняются вдоль всей аномальной зоны, то тело имеет форму, близкую к цилиндру, т.е. размеры по падению сопоставимы с мощностью тела и значительно меньше размеров по простиранию.

Если временные зависимости резко меняются, проводник можно уподобить пластине, размеры по падению которой значительно превышают ее мощность.

Проекция кромки цилиндра располагается в области максимальных значений вдоль профиля.

Проекция кромки тонкого крутопадающего пласта находится между двумя максимумами . При пологом падении тела максимум со стороны лежачего бока может быть очень слабо выражен. В этом случае проекция кромки будет вблизи более резкой ветви кривой . Аналогично определяется проекция верхней кромки мощной пластины.

Если установлено, что проводящее тело можно уподобить пластине, определяется угол падения по формуле:

α = p/2 – φ = p/2 – 0.85lg 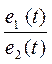, рад. (153)

Расстояние h от пластины до поверхности определяется с точностью 30 – 40%, как половина расстояния между двумя максимумами. Это прием пригоден при R << h, что выполняется при проведении детализационных работ. Чем меньше t, тем точнее h.

Для изометрических тел глубина до центра тела находится графическим способом. На графиках вдоль эпицентрального профиля до центра аномалии откладывается расстояние, равное радиусу петли или половине стороны квадратной петли. Соответствующее этому расстоянию значение принимается за 100%. Расстояние от этой точки до точки, где = 8%, с точностью до 20 – 30% равно Z (рис. 47). Аналогичным образом определяется Z для вытянутых аномалий, вызываемых телами, близкими по форме цилиндру.

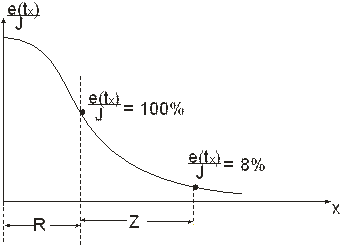
Рис. 47.

Столь же простым графическим приемом можно приближенно оценить мощность пластообразного крутопадающего проводника. По графику вдоль линии, проходящей в крест простирания, определяют:

А = 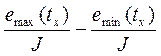. (153)

Расстояние между точкой, где величина минимальна, и точкой, где 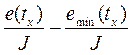= 0.16А, (154) равно с точностью до 20 – 30% мощности пласта.

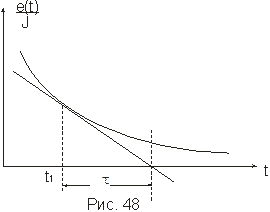
Важнейшим параметром является τ – постоянная времени переходного процесса. τ = gmQ сек. Один из способов ее определения заключается в следующем. Строят временную характеристику. В точке, соответствующей выбранному моменту времени t₁, проводят касательную к кривой . Отрезок по оси времени между t₁ слева и точкой пересечения касательной с осью времени (справа), равен τ(t) (рис. 48).

Определение g_к: τ_к = 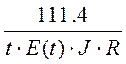, (155)

g_к = 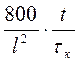, (156) где t – время регистрации переходного процесса, l - ½ стороны петли.

13.О представлении результатов наблюдений в индуктивных методах в виде ρ_к.

В методах электроразведки, использующих постоянные электрические поля, обычно измеряется разность потенциалов, которая приводится к единице силы тока. Это частное 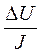умноженное на коэффициент К, который выбирается так, чтобы в однородной среде новая функция равнялась удельному сопротивлению. Затем применяя ту же установку, с тем же выбранным таким образом коэффициентом К, в неоднородной среде, получают кажущееся сопротивление этой неоднородной среды 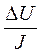К = ρ_к.

В неоднородных средах величина ρ_к, измеренная разными установками, будет различаться. Однако, кажущееся сопротивление является параметром (или приведенной функцией наблюдаемого поля) удобным при решении задач картирования и поисков полезных ископаемых.

В индуктивных методах, использующих переменные поля, измеряются те или иные компоненты поля: амплитуды Н_i, E_i, фазы φ_i^H, φ_i^E вещественной и мнимой компонент поля, большая и малая полуоси эллипса поляризации а и b, и наклон большой полуоси к горизонту φ_а, угол наклона полного вектора магнитного поля к горизонту, отношения амплитуд компонент поля и т.д. Иными словами, в большинстве случаев методы переменного тока являются чисто индикационными. Они служат для выявления осей проводимости, проводящих зон и т.п. на основании графиков перечисленных выше компонент.

Это снижает отдачу методов, не позволяет использовать все возможности, заложенные в них, прежде всего, для решения задач геологического картирования в связи с детальными поисковыми работами.

В методах переменного тока, как уже в некоторых случаях видели, аналогично тому как это делается в методах постоянного тока – целесообразно результаты наблюдений представлять в виде некоторых приведенных параметров типа кажущееся сопротивление.

При выборе параметров необходимо придерживаться основного условия: для однородного и изотропного полупространства, приведенные параметры должны по размерности и численно совпадать с удельным сопротивлением ρ. Тогда для неоднородного пространства получим параметр отвечающий ρ_к.

Как и в случае постоянного тока, в методах переменного тока вычисленное значение ρ_к будет зависеть от типа установки и ее размеров, и кроме того, от характера источника тока и даже от компоненты поля, используемой для вычисления ρ_к.

А.В. Вещев, впервые предложивший вычислять в методах переменного тока так называемый эффективный параметр, рекомендует обозначать соответствующую величину значком 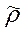, освободив место у ρ для индексов, характеризующих источник поля и измеряемую компоненту, например, 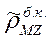, 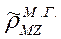обозначают кажущееся сопротивление, определенное по вертикальной составляющей магнитного поля (индексы внизу), соответственно, в поле бесконечно длинного кабеля и магнитного горизонтального диполя (индексы вверху).

Вычисление 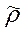в методах переменного тока несколько сложнее, чем вычисление ρ_к в методах постоянного тока. В случаях, когда источником тока является электрический или магнитный диполи, или бесконечно длинный кабель – вектор-потенциал и составляющие поля имеют сложную зависимость от приведенного расстояния р = ϰr, где ϰ – волновое число среды, r - расстояние между источником поля и точкой наблюдения.

Если точки смещения играют незначительную роль, т.е. ϰ² можно считать мнимой величиной, то в условной системе единиц:

р = 0.4p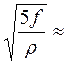r 2.81r 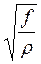, где r – в км, f – в гц, ρ – в Омм.

В случаях, когда источник имеет линейные размеры:

р^/ = рl = 0.4p·r·l· 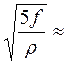2.81·r·l· 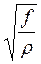, где l – характерная длина питающей линии в км.

В написанных выше формулах величины r (расстояние), частота f, длина l всегда известны. Поэтому, зная р и р₁ можно найти величину кажущегося удельного сопротивления 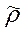. Но для вычисления 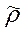необходимо наличие однозначной зависимости между измеряемыми величинами компонент поля и приведенными расстояниями р и р^/. Это условие не во всех интервалах частот и других характеристик соблюдается. Для разных источников поля и различных компонент поля однозначная зависимость от р и р^/ может лежать в разных интервалах f, r и .

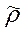Рассмотрим возможность определения 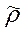в методах, использующих магнитные диполи.

Нормальное поле вертикального и горизонтального магнитного диполей на поверхности однородного проводящего полупространства рассчитаны и рассмотрены нами в соответствующих местах для отдельных компонент поля.

1. Для вертикального магнитного диполя.

H_i = 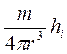, Е_i = 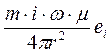(в системе СИ).

В цилиндрической системе координат имеются составляющие H_z, H_r, E_φ.

2. Для горизонтального магнитного диполя.

H_i = 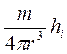. В цилиндрической системе координат есть составляющие H_z, H_φ, H_r (E_i – отсутствует).

В этих формулах, связывающие компоненты магнитного поля с соответствующими магнитными числами, величина 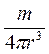характеризует поле диполя в воздухе (первичное поле), а безразмерные величины h_i (i = z, r, φ) и e_φ – выражают изменения поля вследствие применения переменного тока (это так называемые магнитные и электрические числа).

Как видно из соответствующих таблиц, графиков, рассмотренных ниже, для каждой составляющей поля магнитные числа h_i являются многозначными функциями приведенного расстояния р. Они имеют экстремумы. Но вместе с тем, в большинстве случаев возможно определение р по одному из магнитных чисел (h_z, h_r или φ).

Для этого нужно при полевых работах использовать такие расстояния и частоты, при которых весь возможный диапазон изменения 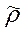приходится на интервал монотонного изменения магнитных чисел (без экстремумов). Из 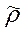= 7.9 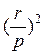f. В случае такого выбора расстояний r и частот f легко определяется 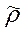по h_i.

А.В. Вещевым выбран другой параметр, откладываемый по горизонтальной оси при расчетах зависимостей h_i от р. Берется 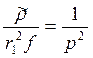с точностью до множителя 7.9, т.е. h_i = f( 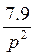), вместо
h_i = f(р²) по Светову.

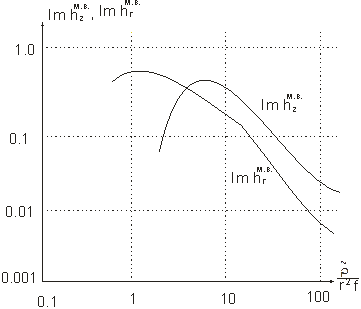
Рис. 49.

Из двух примеров на рис. 49 для поля вертикального магнитного диполя видно, что очевидно, в случае измерения h_z нужно подбирать такие r и f, чтобы 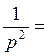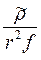лежало в пределах примерно от 10 до 100, при измерении h_r – от 2 – 3 до 100. Очевидно, построение кривых зависимости h_i от 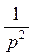удачнее, чем от р², ибо здесь можно сразу получить величину 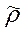с точностью до множителя 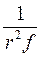, который является постоянным и выбирается исполнителем.

Таким образом, рассмотренные графики позволяют сразу по величине магнитного числа определить .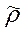

Как показывают формулы и расчеты, увеличение частоты применяемого поля сдвигает диапазон возможных изменений 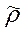в сторону высоких сопротивлений.

Для составляющих Re h_r^М.В. , |h_r|^М.В. диапазон однозначной зависимости составляет от 0.2 до 1000 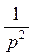, т.е. является широким: 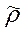может меняться в 1000 раз, не нарушая зависимости однозначной h_i от .

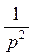Рассчитаны такие же зависимости для высот 50 м и 100 м над поверхностью земли, т.е. для аэроэлектроразведки. При этом оказывается, что при аэроэлектроразведки интервалы однозначной зависимости расширяются в сторону низких сопротивлений. Вычисление 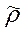на примере метода индукции рассмотрено нами ранее.

Наиболее удобен для вычисления 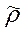низкочастотный интервал. При обычных расстояниях между диполями (r = 50 – 200 м) и ρ среды от единиц до сотен Омм, частоты f не должны превышать 7 – 8 Кгц (в аэроэлектроразведке частоты можно увеличить в 1.5 – 2 раза).

Если говорить об упрощении методики полевых работ при вычислении 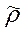, то для этого удобны амплитудные значения |h_r^М.В.| или |h_z^М.В.|. Можно ограничиться измерениями в поле вертикального магнитного диполя – радиальной составляющей магнитного числа h_r, в поле горизонтального магнитного диполя – h_z.

Рассмотрим вариант определения 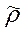по результатам измерения низкочастотных электрических полей в поле электрического диполя.

При определении 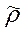используется величина ρ_w = К 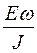, где Е_w - вещественная или мнимая компонента напряженности электрического поля с круговой частотой w или же модуль напряженности электрического поля частоты w. J - сила тока в питающей линии. К – коэффициент, определяемый геометрией установки.

При малых значений приведенных расстояний р имеем:

ρ_w = ρ_к (для постоянного тока в неоднородных средах);

ρ_w = ρ (для постоянного тока в однородных средах).

При больших значениях ρ величина ρ_w не равна ρ и ρ.

Рассмотрим горизонтальный электрический диполь.

E_{r w} = E_r·e_r, E_{φ w} = E_φ·e_φ, e_{i=r, φ} = Re e_i + i·Im e_i, где E_{r w} и E_{φ w} - радиальная и азимутальная составляющие напряженности электрического поля горизонтального электрического диполя, питаемого постоянным током силы J, e_r и e_φ – соответствующие электрические числа, исправляющие E_{r w} и E_{φ w} за счет переменного тока круговой частоты w.

Сопоставляя все эти выражения с выражением для

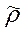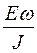= К =К 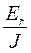, видим 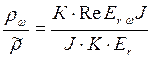= = 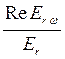=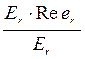Re e_r

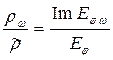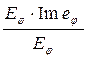= = Im e_φ и т.д.

Рассчитаны кривые Re e_r и Im e_r, Re e_φ и Im e_φ в зависимости от
р = | ϰ |r или также от = .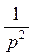

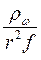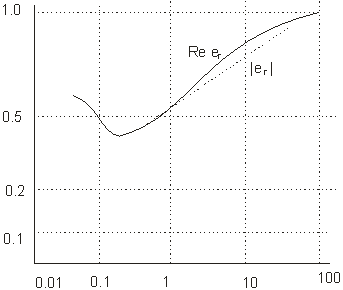
Рис. 50.

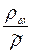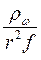Из рис. 50 видно, что зависимость между и , определенные по модулю |e_r| т вещественной компоненте Re E_r, имеют очень близкие значения: в указанном на рисунке интервале 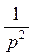они отличаются не более, чем на 5%. При больших значениях 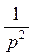отношение 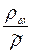>> 1, т.е. можно пользоваться формулами для постоянного тока. Это означает, что здесь ρ_w в пределах точности наблюдений совпадает с удельным сопротивлением ρ.

Совершенно аналогично ведут себя зависимости 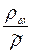от 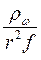для модуля |e_φ| и вещественной компоненты Re E_φ.

Это значит, что модули и вещественные компоненты e_r и e_φ можно использовать для определения 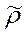во всем диапазоне измерения 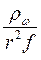, на участках однозначной зависимости (например, на рис. 50 для 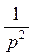от 0.2 до 100).

Отличительной особенностью метода НП является однородность первичного магнитного поля и ослабленность первичного электрического поля в средней части петли, а также медленное убывание первичного поля с глубиной и, следовательно, высокая глубинность исследования. Первичное магнитное поле внутри петли направленно практически вертикально, поэтому наилучшие условия в методе НП создаются для выявления горизонтально- или пологозалегающих проводящих объектов.

Первичное поле вне петли кроме вертикальной составляющей имеет и горизонтальную, значительно превосходящую первую по интенсивности. Поэтому за пределами петли создаются благоприятные условия для выявления крутопадающих проводящих объектов.

Благодаря индуктивному возбуждению полей, однородности первичного поля и измерению в ближней зоне проводящие объекты характеризуются аномалиями магнитного типа, что зачастую делает возможным решение обратной задачи.

Как правило, площадная съемка проводится внутри квадратных петель с длиной сторон 0.5 – 2 км. Различные параметры поля измеряются по параллельным профилям, расположенным на расстоянии 20 – 100 м друг от друга. Профили наблюдений располагаются в крест простирания горных пород и заканчиваются на расстоянии 200 м от токонесущего провода. Расстояние между соседними точками наблюдений меняются от 10 до 50 м и должны быть меньше предполагаемой глубины залегания разведываемых объектов. После отработки планшета петли перемещаются таким образом, чтобы либо один из крайних профилей, либо в нескольких точках наблюдения всех профилей наблюдения повторялись при двух положениях петли.

Поисковые работы по методу НП выполняются в 2 этапа: площадная съемка и детализация аномалий.

При площадной съемке обычно проводятся одночастотные измерения магнитного поля. Рабочая частота выбирается в результате опытных работ и на основании анализа частотных характеристик. Она должна быть такой, чтобы величины амплитудных аномалий приближались к своему асимптотическому значению, а аномалии фазы располагались в области экстремума своей частотной характеристики. Параметры аномалии р в этом случае должны быть в пределах 5 – 10.

На этапе детализации исследуются перспективные в отношении оруденения аномальные участки на 3 – 5 частотах для более точной оценки параметра аномалии и геометрической характеристики объекта.

В результате съемки строятся графики, карты графиков различных параметров поля для одной или нескольких частот. На аномальных точках строятся частотные характеристики.

Интерпретация данных съемки НП делится на качественную, которая сводится к визуальному анализу выявленных аномалий, корреляции их по профилям и сопоставлению их с геологическими данными, и количественную. Количественная интерпретация начинается с определения параметра аномалии р путем сопоставления экспериментальной частотной характеристики с теоретическими графиками вторичного поля. Поделив найденную величину на ω, можно определить величину τ = γμа² проводящего объекта. Нередко τ является основным результатом интерпретации, позволяющим судить о связи аномалии с хорошо проводящим оруденением. Так, значения τ > 0.02 с практически однозначно указывает на наличие массивного сульфидного рудного тела. На достаточно низких частотах аномалии НП могут интерпретироваться как обычные магниторазведочные аномалии при вертикальном намагничении тела. В случае тел простой формы возможно решение обратной задачи – определение его глубины, размеров, проводимости, элементов залегания.