Нормальное поле бесконечно длинного кабеля.

При теоретических расчетах и анализе физических явлений в методе ДК в качестве источника поля принимают весьма длинные заземленные линии, а анализ поля проводят вблизи кабеля. Нормальное поле такого длинного кабеля можно используют при количественной интерпретации.

Особый интерес представляет поле бесконечно длинного кабеля, расположенного на поверхности Земли. Токами смещения в Земле и в воздухе пренебрегают. Ось х совпадает с направлением кабеля. На поверхности Земли (z = 0) рассчитывают потенциал поля А_х, вертикальную составляющую магнитного поля Н_z, горизонтальные составляющие магнитного Н_у и электрического Е_х полей, обусловленные наличием электрического тока в нижнем проводящем полупространстве.

Потенциал и компоненты электромагнитного поля бесконечно длинного кабеля на поверхности Земли (z = 0) определяются по формулам:

Е_х = 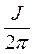wmf(ϰ, y); (107)

H_z = 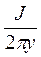f₁(ϰ, y); (108)

H_y = 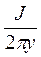f₂(ϰ, y); (109)

A_х = 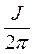f₃(ϰ, y); (110)

где f(ϰ, y), f₁(ϰ, y) - комплексные функции Струве, f₂(ϰ, y), f₃(ϰ, y) – комплексные функции Бесселя.

Для анализа удобно ввести электрические и магнитные числа электромагнитного поля в виде:

e_х = f(ϰ, y) = 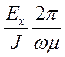; (111) h_z = f₁(ϰ, y) = 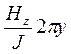; (112)
h_y = f₂(ϰ, y) = 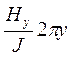. (113)

Рассчитаны и построены графики их амплитуд и фаз (т.е. модулей и аргументов) в зависимости от квадрата приведенного расстояния, т.е. от параметра р² = |ϰ²y²|, где у – расстояние от точки наблюдения до кабеля на поверхности Земли (рис. 16).

На рис. 16 представлены также графики амплитуды А^* и сдвига фаз φ^* для потенциала поля.

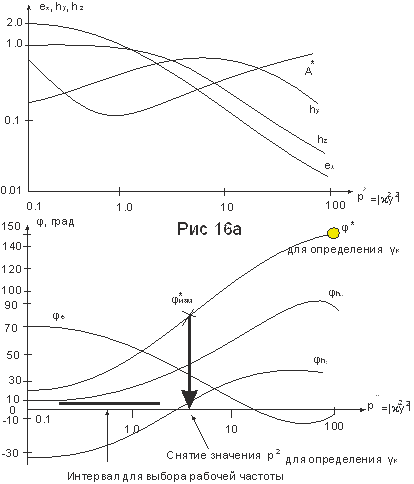
Рис. 16б. Графики амплитуд и фаз потенциала, электрических и магнитных чисел компонент электромагнитного поля БДК.

Рассмотрим поведение поля кабеля в области, где |ϰy| << 1 и где |ϰy| >> 1.

Принято называть зону |ϰy| << 1 ближней или индукционной, а зону |ϰy| >> 1 – дальней или волновой. В воздухе, где ϰ₀ ≈ 0, величина |ϰ₀y| в обеих зонах остается очень малой, поэтому поле на земной поверхности и в воздухе лишено характерных волновых черт не только в ближней, но и в дальней зоне. Приведенная классификация зон имеет реальный смысл только в земле, где в ближней зоне поле квазистационарное, а в дальней зоне, оно приближается к полю плоской волны, распространяющейся вертикально сверху вниз. По графикам электрических и магнитных чисел и их асимптотическим выражениям можно определить основные закономерности поведения поля кабеля.

При |ϰy| << 1 электрическое поле Е_х и вертикальная составляющая магнитного поля Н_z ведут себя также, как в однородном пространстве. При уменьшении расстояния до кабеля величина Е_х растет как логарифм расстояния, а величина Н_z обратно пропорциональна расстоянию, фазовый сдвиг между ними стремится к p/2.

Составляющая магнитного поля Н_у, отсутствующая в однородном пространстве, при убывании расстояния до кабеля стремится к постоянной величине 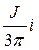ϰ и сдвинута относительно тока в кабеле на угол p/4. При увеличении частоты поля величина Н_у растет пропорционально .

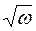При |ϰy| >> 1 компоненты Е_х и Н_z убывают по экспоненциальному закону, горизонтальный компонент магнитного поля Н_у убывает как 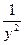, т.е. медленнее, его фаза стремится к углу p/4.

Рассчитаны и построены графики величин, получаемых по методике эллиптически поляризованного поля (рис. 17).

На этих графиках изображены магнитные числа большой и малой полуосей (а^* и b^*), угол наклона большой полуоси эллипса к горизонту (α) и ее фаза (φ_а) относительно тока в источнике. Магнитные числа большой и малой полуосей эллипса поляризации связанны с самими полуосями соотношениями:

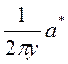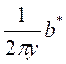а = и b = , (114)

Приведенные величины полностью определяют эллиптически поляризованное тело. При малых значениях р² большая полуось эллипса поляризации наклонена под углом 90⁰ к горизонту, а при увеличении р² величина α стремится к нулю (α ® 0).

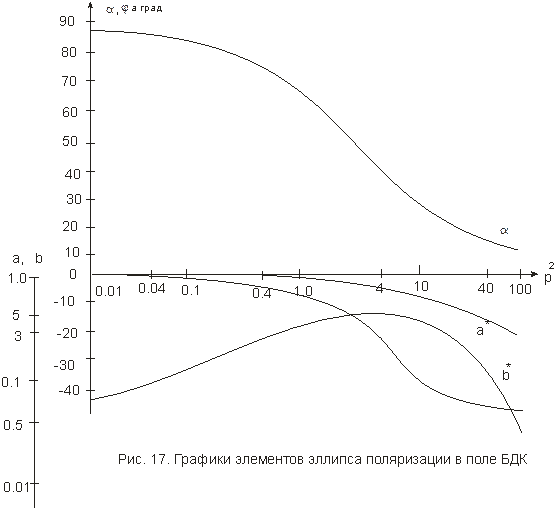
При малых р² величина фазы большой полуоси эллипса поляризации φ_а синфазная с питающим током, а при р² ® 100 величина фазы φ_а ® 45⁰ по отношению к фазе питающего тока.