Круговой цилиндрический проводник в поперечном магнитном поле.

Рассмотрим основные закономерности поведения локального проводника, возбуждаемого низкочастотным гармоническим электромагнитным полем.

Круговой цилиндр радиуса а и проводимости g помещен в однородное переменное магнитное поле напряженностью Н₀, перпендикулярное к оси цилиндра. Во внешней, по отношению к цилиндру области, будет наблюдаться суммарное магнитное поле, которое складывается из первичного внешнего магнитного поля Н₀ и вторичного магнитного поля Н_вт, которое создает проводящий цилиндр. Компоненты напряженности суммарного магнитного поля в цилиндрической системе координат (ось z – совмещена с осью цилиндра) имеют вид:

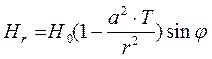, (92)

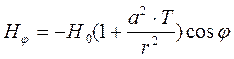, H_z = 0, (93)

Т = J₂(ϰ,a)/J₀(ϰ,a), (94)

где J₀(x), J₂(x) – цилиндрические функции Бесселя 1-го рода нулевого и второго порядка,

φ – угол, отсчитываемый от направления, перпендикулярного к Н₀.

Магнитные проницаемости цилиндра и вмещающей среды положим равными m₀.

Вторичное магнитное поле от цилиндра определяется величиной Т·а², зависящей от параметров проводника, частоты поля и координат точки наблюдения.

Из приведенных на рис. 5 графиков видно, что в области малых параметров α вторичное магнитное поле сдвинуто по фазе на p/2 и растет пропорционально частоте. При повышении частоты мнимая часть напряженности магнитного поля достигает экстремума при α = 12, а затем убывает. При больших значениях α убывание Im Н_вт обратно пропорционально .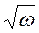

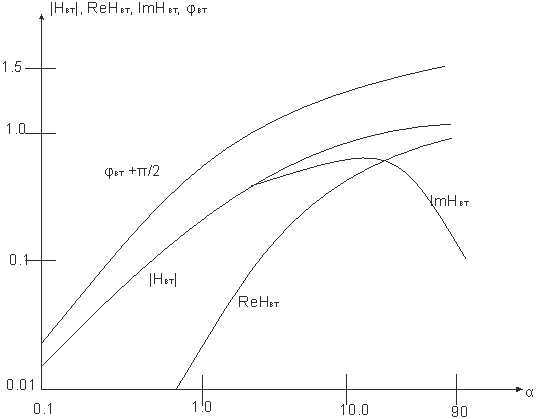
Рис. 5.

Действительная часть напряженности магнитного поля Re H_вт в области больших значений α стремится к 1. При увеличении частоты вторичное магнитное поле становится противофазным с возбуждающим магнитным полем Н₀.

Все отмеченные выше закономерности можно качественно описать формулой:

Н_вт = ϰ · 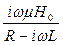, (95)

где R – эквивалентное омическое сопротивление цилиндра,

L – индуктивность цилиндра по отношению к вихревым токам в нем.

Определение параметра α по частотным характеристикам вторичного поля.

Для некоторых геометрических тел правильной формы теоретически рассчитаны и построены частотные характеристики вторичного магнитного поля (на рис. 5 приведены частотные характеристики для кругового цилиндра радиуса а и проводимости g).

Как видно из рисунка 5, частотная характеристика амплитуды вторичного поля |H_вт| имеет две асимптоты.

1. В области малых параметров α – асимптота расположена под углом в 45⁰ к оси абсцисс (наблюдается прямо пропорциональная связь вторичного поля с параметром α).

2. В области больших параметров α частотная характеристика выходит на горизонтальную асимптоту. Это значит, что аномалия от любого тела при увеличении частоты, т.е. возрастания α, стремится к аномалии от идеального проводника той же формы.

Частотные характеристики амплитуды вторичного поля |H_в | строятся в билогарифмическом масштабе: по оси абсцисс откладывают параметр α = gmwQ = 2pgmQf = Kf; по оси ординат – амплитуду вторичного поля |H_в |.

Удобство двойного логарифмического масштаба при построении отношений в зависимости от α состоит в следующем.

а) Изменение величины вторичного поля Н_вт за счет изменения точки наблюдения поля или глубины залегания объекта приводит к сдвигу частотной характеристики по вертикали.

б) Изменение одного из сомножителей, входящих в α (например, g) и не влияющих на величину вторичного поля Н_вт приводит к сдвигу частотных характеристик поля по горизонтали.

Две частотные характеристики поля будут считаться совпадающими наилучшим образом, если они совмещаются на билогарифмическом бланке в области обеих асимптот. С этой точки зрения частотные характеристики амплитуды вторичного магнитного поля от тел произвольной формы могут быть совмещены друг с другом, если пренебречь их расхождением в промежуточной части.

Приняв частотную характеристику одного из известных тел за основную и построив ее в зависимости от параметра α = gmwa² (a² = Q) можно на основе совмещения с ней частотных характеристик для тел различной формы найти для них соответствующее выражение Q.

Найденные таким образом параметры α интерпретируют по формулам:

1. α = 1/2gmw 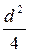- для шара или изометрического проводника.

2. α = gmw 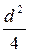- для кругового цилиндра или сильно вытянутого по простиранию проводника с изометрическим сечением.

3. α = 2gmw 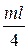- для пласта или сильно вытянутого по простиранию проводника с не изометрическим сечением.

В этих формулах: d – диаметр рассматриваемого шара или цилиндра, m – мощность пласта, l – размер пласта по падению.

Рассмотрим пример интерпретации результатов абсолютных измерений вертикальной составляющей напряженности магнитного поля в методе НП.

Пусть на съемочном планшете в результате многочастотных амплитудно-фазовых измерений выделена аномалия вертикальной составляющей магнитного поля. Из измеренного суммарного магнитного поля необходимо выделить вторичное магнитное поле возбужденное проводником.

При измерении амплитуды вертикальной составляющей магнитного поля в методе НП выражение для вторичного поля можно брать в виде:

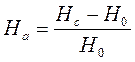, (96)

где Н_с – суммарное магнитное поле; Н₀ – поле принятое за нормальное, которое совпадает с полем применяемого источника в воздухе.

Если нормальное поле известно, то вторичное аномальное поле можно определять построением векторной диаграммы на фоновой плоскости вида:

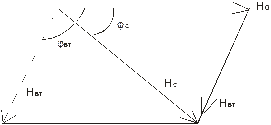
Рис. 6.

Определение амплитуды вертикальной составляющей вторичного магнитного поля производится на каждой частоте, а на основании этих данных строят зависимость |Н_вт| от частоты, т.е. строят частотную характеристику |Н_вт|. Частотную характеристику |Н_вт| строят на таком же логарифмическом бланке, на каком была построена параметрическая кривая |Н_вт| для кругового цилиндра.

По оси абсцисс откладывают частоту поля f, по оси ординат соответствующее значение Н_а = 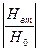. Эта кривая накладывается на палеточную так, чтобы оси были параллельны, и добиваются их совмещения в области асимптот.

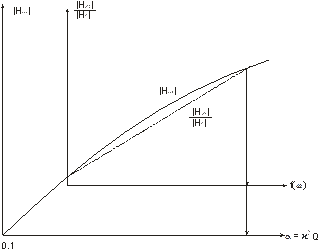
Рис. 7.

Затем устанавливают соответствие между значениями параметров и соответствующими значениями частот, т.е. с оси абсцисс палеточной кривой и практической кривой снимают соответствующие α и f(w).

Важно найти раздельно величины электропроводности g тела и его характерных размеров Q.

Для трех видов тел (шара, цилиндра и пласта) имеем:

α = gmw 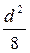; α = gmw 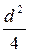; α = gmw 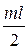(97)

Общая формула: α = gmwQ, где Q = 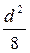- для шара, Q = 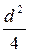- для цилиндра, Q = 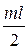- для пласта.

Поэтому дальше из полученного с палетки параметра α исключают частоту и получают приведенный параметр τ:

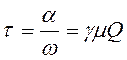. (98)

Само по себе значение еще не позволяет делать выводы о количественных характеристиках аномального объекта, ибо содержит произведение неизвестных физических свойств проводника gm на его размеры Q.

Обычно считают, что m известно, а именно, полагают, что рудные тела немагнитные. Кроме того обычно известны пределы, в которых могут находиться размеры интересующих нас тел и их ориентировочная форма (изометрическое, линзовидное).

Тогда можно определить пределы изменения τ, и по величине τ оценить проводимость аномального объекта.

Иногда величина приведенного параметра τ настолько значительна (τ = 0.02 и более), что практически однозначно указывает на наличие очень высокой проводимости объекта (например, массивных колчеданных руд).

Величина 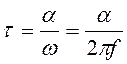имеет размерность времени и является характерным временем для данного аномального объекта.

Значение параметра α можно находить по частотной характеристике Н_а = 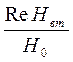. Эта частотная характеристика в области низких значений имеет асимптоту, идущую на логарифмическом бланке под углом 63⁰31^/ к оси абсцисс, что отражает пропорциональность Re H_вт квадрату частоты. В области высоких частот она также выходит на горизонтальную асимптоту.

Для не слишком больших значений аномальных эффектов обычно реальная часть вторичного поля близка по значению амплитудной аномалии вертикальной составляющей магнитного поля НП:

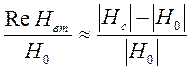. (99)

Это позволяет определять параметр α на основе многочастотных чисто амплитудных измерений.

При этом на каждой частоте находятся величины аномалии

Н_а = 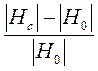, (100)

по которым строится частотная характеристика Н_а. Эта характеристика по ранее приведенным правилам совмещается с палеточной характеристикой 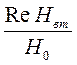кругового цилиндра, после чего устанавливается соответствие частот и параметров.

Точно также может быть использована и частотная характеристика 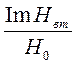. В области высоких частот соответствующая кривая идет под углом -28⁰40^/ к оси абсцисс, т.е. обратно пропорционально 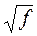. Сопоставление результатов измерений с данной частотной характеристикой производится по приведенным выше правилам.

Для не слишком больших значений аномалий мнимая часть горизонтальной составляющей магнитного поля близка по значению малой полуоси эллипса поляризации (b), а нормальное поле – близко по значению большой полуоси (а).

Поэтому 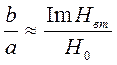(101)

и интерпретация аномалий полученных по методике эллиптически поляризованного поля (ЭПП) может производиться на основе сопоставления частотных характеристик отношений с частотной характеристикой мнимой части вторичного поля.

Можно распространить описанную выше методику интерпретации на методику двух горизонтальных рамок. При этом величина изменяется с частотой как величина 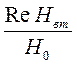, а величина аномалии (φ_с – φ_n) изменяются с частотой как величина . (102)

Для использования частотных характеристик необходимо предварительно перевести отношения амплитуд 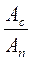из единиц децибел в единицы непры (А_неп = ), а сдвиг фаз из угловых градусов в радианы ( 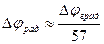) (103).

Пользуясь этими выражениями как декартовыми компонентами вторичного поля, можно графически определить его полярные компоненты, т.е. амплитуду и фазу вторичного поля.

В случае небольших значений аномалий результаты измерений по методике скрещенных рамокможно представить в виде:

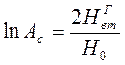, (104)

т.е. результат измерения в методике скрещенных рамок близок к удвоенной величине отношения горизонтальной составляющей вторичного поля к первичному полю.

Имеется также способ определения параметра α по фазе вторичного поля на фиксированной частоте.

Фазовые характеристики величин вторичного поля от тел разной формы довольно сходны между собой, что позволяет и в этом случае ввести обобщенные фазовые характеристики для тел произвольной формы. Определяя по амплитудно-фазовым измерениям фазу вторичного поля на некоторой частоте, можно по обобщенной фазовой характеристике найти соответствующее значение параметра α = 2pgmQf.

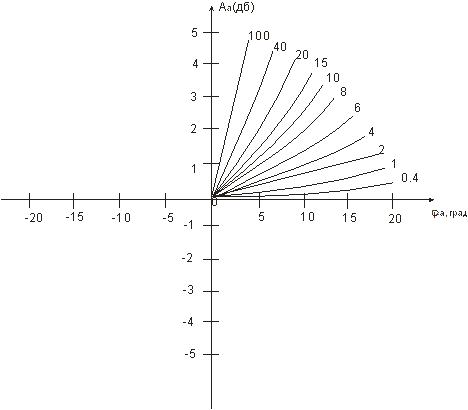
Рис. 8.

Пользуются специальной палеткой, непосредственно по результатам измерений фазы находится параметр вторичного поля α (рис. 8). Кривые на этой палетке индексированы значением параметра α. Наиболее точно параметр определяется в области пропорционального роста φ_вт с частотой, т.е. при значениях α < 10. Данный способ определения параметра α может быть применен к результатам измерений по методикам двух горизонтальных или скрещенных рамок.

Интерпретация результатов электроразведки на переменном токе принципиально отличается от интерпретации других геофизических методов, использующих потенциальные поля (гравиразведка, электроразведка на постоянном токе).

В электроразведке на переменном токе для некоторых случаев (когда объект уподоблен сфере или круговому цилиндру) возможно полное решение обратной задачи, т.е. на основе наблюдений поля незаземленной петли на аномальном участке можно найти электропроводность, характерные размеры и условия залегания аномального объекта.