Нормально поле круглой петли.

При интерпретации результатов наблюдений по методу НП необходимо знать величины горизонтальной составляющей электрического и вертикальной составляющей магнитного полей, для круглой петли радиуса R, лежащей на поверхности однородного проводящего полупространства (z = 0) с волновым числом ϰ.

Внутри петли амплитуды E_φ и H_z с ростом |ϰ²R²| убывают медленнее, чем вне петли. Для малых значений |ϰ²R²| амплитуда электрического компонента растет пропорционально величине r/R (r – расстояние от центра петли до точки измерения).

Сдвиги фаз H_z и E_φ относительно тока J при заданном |ϰ²R²| меняется внутри петли весьма незначительно, а разность фаз составляющих E_φ и H_z для всех значений |ϰ²R²| близка к p/2.

Вне петли разность фаз электрической и магнитной составляющих меняется в довольно широких пределах с изменением |ϰ²R²| и расстояния от петли.

При |ϰR| << 1 и р = | ϰr| ® 0 влияние проводящего пространства уменьшается и поле внутри петли стремится к полю в воздухе (или в высокоомных породах).

Амплитуды электрической и магнитной составляющих поля определяются в виде:

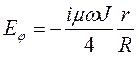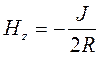; . (82)

Импеданс поля 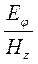выражается формулой:

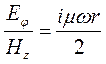. (83)

В центре петли при r = 0 электрическая составляющая поля равна 0, а магнитная составляющая поля определяется в виде:

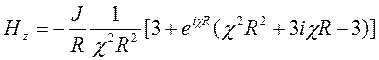. (84)

При малых и больших значениях р = |ϰr| можно пользоваться приближенными выражениями для магнитного числа h_z вертикальной компоненты магнитного поля:

Re h_z = 1- 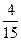p³; Jm h_z = 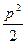при р << 1; (85)

Re h_z = -2p²e^-pcos p; Jm h_z = 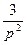при р >> 1; (86)

где h_z = 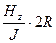- комплексная величина.

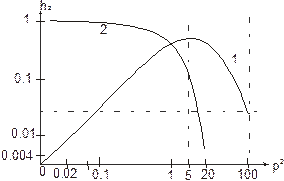Исходя из графиков действительной и мнимой части магнитного числа поля (рис. 1) видно, что в области малых значений р поглощение поля в нижнем проводящем полупространстве невелико и действительная часть h_z (кривая 2) стремится к единице, а мнимая часть h_z (кривая 1) растет пропорционально частоте. Мнимая составляющая магнитного числа имеет максимум при р = 5. В области больших значений р поглощение поля значительное и действительная часть h_z резко убывает до 0, а мнимая часть h_z стремится к 0 как 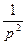монотонно.

Рис. 1.