Решение уравнений Максвелла для установившегося переменного электромагнитного поля.
Полагая в 1 уравнении Максвелла 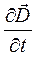 = 0, мы, тем самым, сужается область рассмотрения э/м полей установившимися процессами. Пусть отсутствуют объемные заряды δ и сторонние поля.
= 0, мы, тем самым, сужается область рассмотрения э/м полей установившимися процессами. Пусть отсутствуют объемные заряды δ и сторонние поля.
В этом случае система уравнений Максвелла имеет вид:
rot 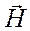 =
= 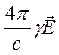 . (22)
. (22)
rot 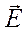 =
= 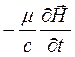 . (23)
. (23)
div 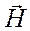 = 0. (24)
= 0. (24)
div 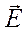 = 0. (25)
= 0. (25)
Переменные электромагнитные поля, описываемые этими уравнениями, могут быть как периодическими полями, так и апериодическими полями.
В индуктивных методах электроразведки изучаются в основном периодические поля. Переменные электромагнитные поля, с которыми чаще всего имеют дело в электроразведке, изменяются по законам, близким к законам гармонических колебаний.
Всякий периодический процесс, согласно преобразованиям Фурье, разлагается на сумму гармонических процессов, которые можно представить в виде гармонических колебаний (гармоник):
a·sin(ωt + φ) или a·cos(ωt + ψ), (26)
где а – амплитуда соответствующей гармоники, ω – круговая частота (ω = 2πf), t – время, φ и ψ – начальные фазы.
Аргументы у синуса и косинуса, т.е. (ωt + φ) и (ωt + ψ), называют фазами колебаний.
Поскольку представление гармонического колебания выражениями, содержащими синус и косинус равноценны, то обычно рассматривают выражение содержащее косинус. Вместо использования тригонометрических функций в записи колебания удобнее перейти к комплексной форме записи колебания.
Согласно формуле Эйлера:
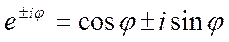 , (27)
, (27)
всякий гармонический процесс (колебание) можно записать в виде:
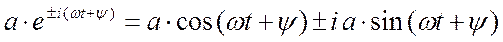 (28)
(28)
Вещественная часть комплексного числа Re( 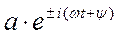 ) представляет собой гармоническое колебание, записанное в тригонометрической форме, т.е.
) представляет собой гармоническое колебание, записанное в тригонометрической форме, т.е. 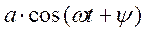 . Поэтому показатель степени экспоненты можно выбрать с любым знаком. Для удобства возьмем минус. Тогда гармонически изменяющийся процесс представляется в виде:
. Поэтому показатель степени экспоненты можно выбрать с любым знаком. Для удобства возьмем минус. Тогда гармонически изменяющийся процесс представляется в виде:
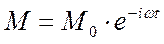 , (29)
, (29)
где амплитуда М0 может быть как действительной, так и комплексной величиной.
Комплексная запись гармонического процесса позволяет пользоваться удобным символическим методом вычислений, который заключается в том, что для взятия производной n – го порядка по времени от функции 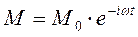 достаточно эту функцию М умножить n раз на величину (-iω).
достаточно эту функцию М умножить n раз на величину (-iω).
Например:
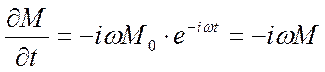 , (30)
, (30)
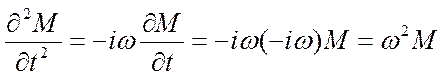 , (31)
, (31)
Учитывая вышесказанное, гармонически меняющееся электромагнитное поле можно написать в виде:
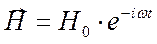 , (32)
, (32)
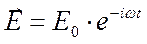 . (33)
. (33)
Тогда система уравнений Максвелла для комплексных амплитудных векторов 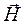 и
и 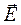 примет вид:
примет вид:
rot 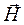 =
= 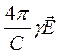 + (-iω)
+ (-iω) 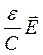 = (
= ( 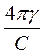 -
- 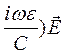 =
= 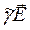 , (34)
, (34)
rot 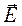 =
= 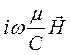 =
= 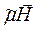 , (35)
, (35)
div 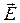 = 0, (36)
= 0, (36)
div 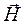 = 0. (37)
= 0. (37)
Чтобы от комплексных амплитудных векторов 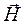 и
и 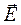 в системе Максвелла перейти к полным выражениям величины поля, надо их умножить на множитель е-iωt.
в системе Максвелла перейти к полным выражениям величины поля, надо их умножить на множитель е-iωt.
В системе уравнений Максвелла символами 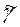 и
и 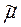 обозначены комплексная электропроводность и комплексная индуктивность (комплексная магнитная проницаемость).
обозначены комплексная электропроводность и комплексная индуктивность (комплексная магнитная проницаемость).
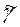 =
= 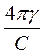 -
- 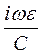 , (38)
, (38)
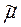 =
= 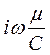 . (39)
. (39)
Применим операцию div к уравнениям (34) и (35), т.е. к уравнениям: rot 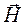 =
= 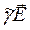 и rot
и rot 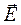 =
= 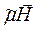
В результате, получим:
div rot  =
= 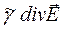 , (40)
, (40)
div rot 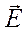 =
= 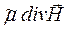 . (41)
. (41)
Воспользуемся формулами:
div 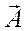 = (
= (  ·
· 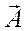 ) =
) = 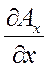 +
+ 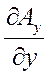 +
+ 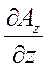 ; (42)
; (42)
rot 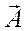 = (
= ( 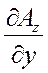 -
- 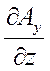 )
) 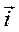 + (
+ ( 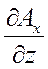 -
- 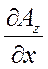 )
) 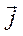 + (
+ ( 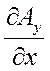 -
- 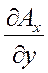 )
) 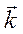 . (43)
. (43)
В результате получим:
div rot 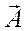 =
= 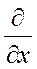 (
( 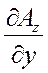 -
- 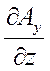 ) +
) + 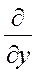 (
( 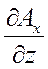 -
- 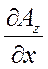 ) +
) + 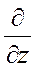 (
( 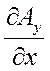 -
- 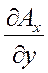 ) =
) = 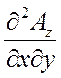 -
- 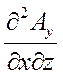 +
+ 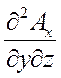 -
- 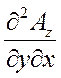 +
+ 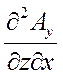 -
- 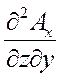 = 0. (44)
= 0. (44)
Или запишем в виде:
div rot  =
= 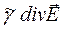 = 0, (45)
= 0, (45)
div rot 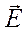 =
= 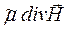 = 0, (46)
= 0, (46)
Откуда следует, что 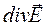 = 0;
= 0; 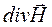 = 0. (47)
= 0. (47)
Таким образом, из первого и второго уравнений системы Максвелла, получаем, соответственно, 3 и 4 уравнения той же системы.
Следовательно, достаточно найти решения уравнений системы (34) и (35), т.е.
rot  =
= 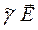 , (48)
, (48)
rot 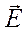 =
= 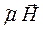 . (49)
. (49)
Эти уравнения являются основными уравнениями гармонического поля в однородной среде.
Приведем уравнения (48) и (49) к форме удобной для их решения.
Для этого применив к ним вихревую дифференциальную операцию, т. е.
rot rot  =
= 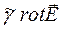 , (50)
, (50)
rot rot 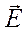 =
= 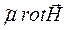 . (51)
. (51)
Подставим в правую часть уравнений (50) и (51) значения rot 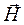 и rot
и rot 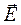 из выражений (48) и (49).
из выражений (48) и (49).
В результате получим:
rot rot  =
= 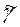
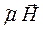 , (52)
, (52)
rot rot 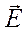 =
= 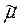
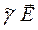 , (53)
, (53)
Введем обозначение: 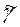
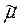 =
= 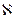 2. Где
2. Где 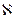 =
= 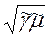 - волновое число.
- волновое число.
Таким образом, получим:
rot rot  =
= 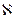 2
2 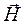 , (54)
, (54)
rot rot 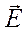 =
= 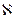 2
2 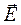 . (55)
. (55)
Так как операция rot, дважды примененная к вектору 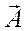 равна:
равна:
rot rot 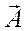 = grad div
= grad div 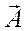 - Δ
- Δ 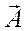 , (56)
, (56)
то выражения (54) и (55) примут вид:
rot rot  = grad div
= grad div  - Δ
- Δ  , (57)
, (57)
rot rot 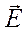 = grad div
= grad div 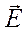 - Δ
- Δ 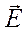 . (58)
. (58)
Так как div  = 0 и div
= 0 и div 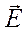 = 0, то получим: (59)
= 0, то получим: (59)
rot rot  = - Δ
= - Δ  , (60)
, (60)
rot rot 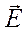 = - Δ
= - Δ 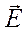 . (61)
. (61)
После подстановки уравнений (60) и (61) в систему уравнений (54) и (55) получим волновые уравнения для магнитного  и для электрического
и для электрического 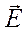 полей вида:
полей вида:
Δ  = -
= - 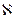 2
2 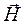 , (62)
, (62)
Δ 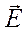 = -
= - 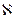 2
2 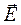 . (63)
. (63)
Оба волновые уравнения и для  и для
и для 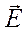 идентичны.
идентичны.
Волновые уравнения (62) и (63) являются векторными уравнениями.
Магнитные и электрические компоненты переменного электромагнитного поля являются компонентами единого электромагнитного поля. Они взаимно зависимы и связаны посредством основных уравнений поля:
rot  =
= 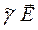 , (48)
, (48)
rot 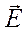 =
= 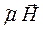 . (49)
. (49)
Вместо шести уравнений достаточно решать 3 волновых уравнения для трех независимых компонент вектора напряженности магнитного поля  или вектора напряженности электрического поля
или вектора напряженности электрического поля 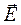 .
.
Рассмотривается вектор напряженности магнитного поля  , который удовлетворяет волновому уравнению:
, который удовлетворяет волновому уравнению:
Δ  = -
= - 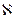 2
2  (64)
(64)
Физический и геологический смысл волнового числа 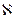 .
.
Волновое число 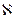 имеет очень большое значение в индуктивных методах разведки.
имеет очень большое значение в индуктивных методах разведки.
Ранее определили, что 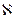 2 =
2 = 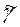 ·
· 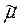 , (65)
, (65)
где 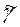 =
= 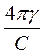 -
- 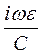 - комплексная электрическая проводимость,
- комплексная электрическая проводимость, 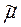 =
= 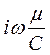 - комплексная индуктивность.
- комплексная индуктивность.
Тогда
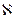 2 =
2 = 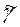 ·
· 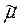 = (
= ( 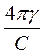 -
- 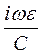 )
) 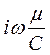 =
= 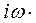
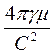 -
- 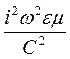 =
=
= 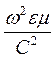 (
( 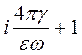 ), (66)
), (66)
Откуда 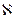 =
= 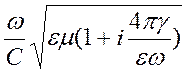 , (67)
, (67)
где ω = 2πf, С – скорость света в вакууме.
Рассмотрим физический смысл величины 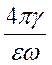 , (68)
, (68)
входящей в выражение для волнового числа (67).
Вернемся к выражению для 1-го уравнения Максвелла в основной системе уравнений Максвелла (17).
rot  =
= 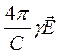 +
+ 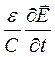 или (69)
или (69)
rot  =
= 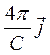 +
+ 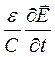 . (70)
. (70)
В случае гармонически меняющегося поля 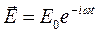 1-ое уравнение Максвелла имеет вид:
1-ое уравнение Максвелла имеет вид:
rot  =
= 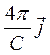 - iω
- iω 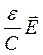 =
= 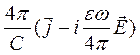 . (71)
. (71)
В последнем выражении 1 слагаемое 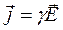 - плотность тока проводимости. Второе слагаемое должно иметь ту же размерность, что и первое, т.е. должно являться плотностью тока.
- плотность тока проводимости. Второе слагаемое должно иметь ту же размерность, что и первое, т.е. должно являться плотностью тока.
Максвелл назвал его током смещения (связанным с процессами, определяемыми диэлектрическими свойствами среды).
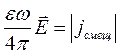 . (72)
. (72)
Тогда выражение (71) можно записать в виде:
rot  =
= 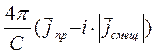 . (73)
. (73)
Итак, имеем:
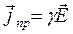 , (74)
, (74)
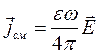 . (75)
. (75)
Найдем их отношение:
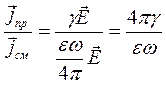 , (76)
, (76)
Получили второе слагаемое под квадратным корнем в выражении волнового числа (67).
Рассмотрим квадрат волнового числа:
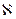 2 =
2 = 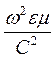 (
( 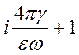 ).
).
В этом выражении 2-ое слагаемое есть отношение токов проводимости к токам смещения.
Рассмотрим два случая.
1. Если среда имеет очень высокую проводимость, т.е. γ >> 1,
следовательно, 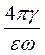 >> 1. Тогда в выражении
>> 1. Тогда в выражении 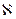 2 =
2 = 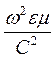 (
( 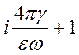 )
)
можно пренебречь 1 в скобках, в результате получим:
 2 =
2 = 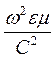
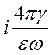 = i
= i 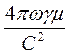 , (77)
, (77)
приняв ω = 2πf, получим:
 2 = i
2 = i 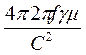 = i
= i 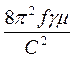 . (78)
. (78)
Основное значение в изучаемом электромагнитном поле будут иметь токи проводимости.
2. Если в среде γ – очень малая величина, то 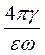 << 1 и с достаточной степенью точности
<< 1 и с достаточной степенью точности 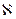 2 =
2 = 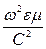 . В этом случае главную роль в изучаемом электромагнитном поле будут играть токи смещения.
. В этом случае главную роль в изучаемом электромагнитном поле будут играть токи смещения.
В частном случае, в идеальном диэлектрике, когда γ = 0, получим точное значение:
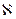 =
= 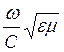 . (79)
. (79)
В воздухе, где μ = 1, ε = 1, получим:
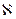 =
= 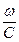 . (80)
. (80)
Подсчитывая значение 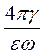 для различных частот можно определить, в каких случаях основную роль играют токи проводимости, а в каких – токи смещения.
для различных частот можно определить, в каких случаях основную роль играют токи проводимости, а в каких – токи смещения.
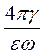 =
= 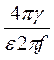 =
= 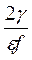 . (81)
. (81)
При низких частотах (до 104 герц) во всех породах преобладают токи проводимости. Лишь при частотах в миллионы герц влияние токов смещения становится заметным во всех породах.
Дата добавления: 2021-05-28; просмотров: 500;











