Закон Ома для участка цепи, содержащего ЭДС

Рассмотрим участок цепи, содержащий сопротивление и ЭДС (рис. 1.14).

Рис. 1.14

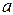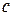Разность потенциалов между точками и равна напряжению

.

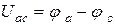Выразим потенциал точки 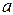через потенциал точки 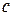. С этой целью сна­чала выражаем потенциал точки 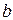через потенциал точки 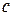, затем потенциал точки 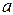– через потенциал точки 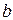(учитывая при этом, что ток протекает от бо­лее высокого потенциала к более низкому и направление действия ЭДС указы­вает на возрастание потенциала).

Для схемы на рис. 1.14 а

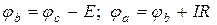
или

.

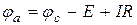Тогда

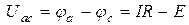. (1.24)

Для схемы на рис. 1.14 б:

или

.

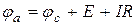Тогда

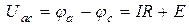. (1.25)

Из уравнения (1.24) для схемы (рис. 1.14 а)

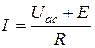. (1.26)

Из уравнения (1.25) для схемы (рис. 1.14 б)

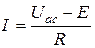. (1.27)

В общем случае

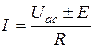. (1.28)

Последнее уравнение выражает в математической форме закон Ома для уча­стка цепи, содержащего ЭДС.

Законы Кирхгофа

Законы Кирхгофа устанавливают соотношения между токами и напряже­ниями в разветвленных электрических цепях произвольного типа.

Первый закон Кирхгофа вытекает из закона сохранения заряда. Он состоит в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю

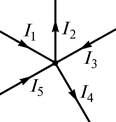Рис. 1.15

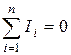, (1.29)

где 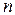– число токов, сходящихся в данном узле.

Например, для узла электрической цепи (рис. 1.15) уравне­ние по первому закону Кирхгофа можно записать в виде

.

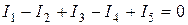В этом уравнении токи, направленные к узлу, приняты поло­жительными.

Второй закон Кирхгофа: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгеб­раической сумме ЭДС в этом контуре

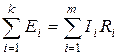, (1.30)

где k – число источников ЭДС; 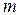– число ветвей в замкнутом контуре; 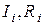– ток и сопротивление 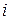-й ветви.

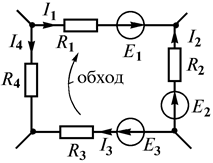Рис. 1.16

Так, для замкнутого контура схемы (рис. 1.16)

.

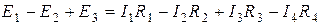Замечание о знаках полученного уравнения:

1) ЭДС положительна, если ее направление совпа­дает с направлением произвольно выбранного об­хода контура;

2) падение напряжения на резисторе положи­тельно, если направление тока в нем совпадает с на­правлением обхода.