Эйлеровы цепи, циклы, котнуры.
Простой цикл, соединяющий все рёбра графа, был назван эйлеровым.
Теорема 1: Конечный граф G(x) является эйлеровым, когда он связан и все его локальные степени чётны.
Необходимость первого условия очевидна; для второго условия – если в процессе движения попали в одну и ту же вершину, то каждому входящему ребру будет соответствовать своя вершина.
Достаточность: Предположим, граф связен и все его локальные степени чётны, будем строить цепь до тех пор, пока это возможно. Остановимся в начальной вершине, так как локальная степень нечётна. Предположим, что цепи содержат не все рёбра, поскольку граф связен, то существует хj , которое инцидентна рёбрам графа. Граф G(x) имеет все чётные локальные степени.
Теорема 2: Пусть G(x) конечный, связный неориентированный граф, имеющий к – вершин с нечётной степенью. Тогда минимальное число непересекающихся по рёбрам простых цепей, покрывающих этот граф = к\2.
Каждая вершина нечётной цепи должна быть концом цепи. Общее число цепей, не больше, чем к\2. Этого количества цепей достаточно для покрытия графа.
Теорема 3: Пусть G(x) конечный связный ориентированный граф. Для того, чтобы существовал простой контур, содержащий все рёбра G(x), необходимо и достаточно, чтобы полустепени захода и исхода совпадали для каждой вершины, то есть
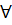 х
х 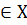
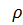 ’(х) =
’(х) = 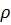 ”(х)
”(х)
Дата добавления: 2016-06-05; просмотров: 2985;











