Определине путей и кратчайших путей в графах.

Существует несколько алгоритмов о решении задач о лабиринте.

1) Алгоритм Тарри. Каждое ребро графа проходит дважды в каждом из двух напралений.

Правило 1: не проходить дважды по одному и тому же ребру в одном и том же направлении.

Правило 2: находясь в вершине x_j не двигаться по ребру. Приведшему в эту вершину один раз, если имеются другие возможности.

Можно показать, что остановка из-за невыполнения этого алгоритма произойдёт в x₀ , причём все рёбра графа к этому времени будут пройдены во всех направлениях по одному разу.

2) Алгоритм Бержа.

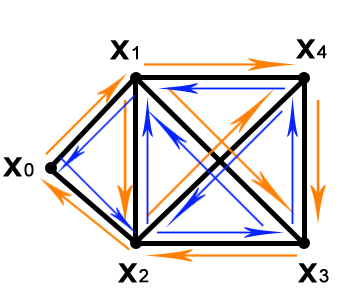
Алгоритм прост, но не экономичен.

Л

В ряде случаев, когда известен тип задачи, алгоритм Тарри можно рассматривать в упрощённом виде: идём столько раз вперёд, пока не попадём в висящую вершину, попадая в неё поворачиваем в сторону не пройденного пути, снова попадаем в висящую вершину, пока не попадём в нужную. Пусть соответствует однократному графу (то есть прохождение одного раза).

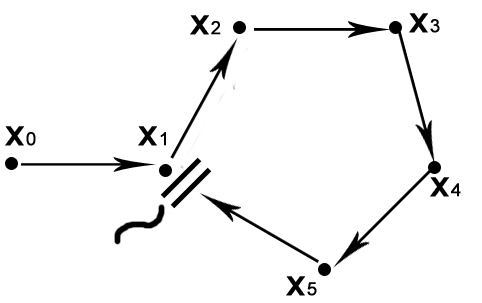Отсечение (введение ещё одной вершины, не совпадающей с первой).

Граф G(x) представляет собой граф с нагруженными рёбрами, под длиной пути 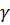подразумевается сумма мер.

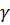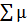= (x_i , x_j), где (x_i , x_j) принадлежат .

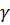В особый класс выделяются задачи для графа с ненагруженными рёбрами, причём такой граф считается графом с нагруженными рёбрами, длина пути которого составит

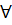i, j (µ(x_i , x_j)).

Алгоритм 1: Начиная от х₀ просматриваем сначала все вершины смежные с х₀ путём. Состоящим из одного ребра. У каждой из этих вершин записываем по мере от каждой вершины до х₀. На следующем шаге просматриваем все вершины достижимые из х₀ двухрёберными путями, и опять в каждой вершине записываем её расстояние до вершины х₀. Очевидно, возможны случаи, когда в какую-нибудь вершину мы попадаем дважды. В таком случае (если в вершину идёт несколько путей) в этой вершине записывается мера кратчайшего из путей и указывается по какому пути достигнута.

Допустим, на некотором шаге попали в вершину х_к по пути длинной М, далее исключим из рассмотрения все вершины не совпадающие с х_к, для которых длина пути М 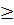М₁ (так как через эти вершины нет более короткого пути). После этого на оставшемся графе продолжаем осмотр путей описанным способом. Возможно, что на некотором шаге мы опять попадем в х_к по пути М₂ < М₁. Тогда исключим все просмотренные вершины, не совпадающие с х_к и длиной < М₁. Этот алгоритм представляет собой один из вариантов исследования задачи операции методов динамического программирования.

Алгоритм Форда: Этот алгоритм предназначен для нахождения кратчайшего пути в ориентированном графе из х₀ в х₁.

На первом шаге каждая вершина х_i помечается индексом 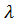_i. Ищем дугу

(х_{i ,} x_j) для которой выполняется неравенство:

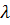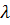_j – _i 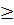µ(x_i , x_j).

Выполним эту операцию несколько раз, причем 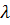_j – уменьшается, а индексы установлены до некоторого уровня. Ищем х_р – смежную с вершиной х_n­ и такую для которой λ_n-λ_p= µ(x_р , x_n).

Пусть х_р – последняя вершина, в которой удалось уменьшить индекс, далее переходим к вершине х_s, смежной с вершиной х_р­ такую что λ_p - λ_s = µ(x_s , x_p). Такая вершина найдётся из аналогичных рассуждений и так далее. В результате последовательность индексов λ_n , λ_p , λ_s … - убывающая, соответственно на каком-то из шагов мы попадём в вершину (x_p)_к+1 = х₀ для которой 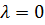. Справедливо следующее утверждение: установившееся значение 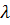_n есть длина кратчайшего пути, ведущего из х₀ в х_n.

Доминирование.