Алгоритм построения

1. Задать проекции элементов определителя (рис. 2-44)

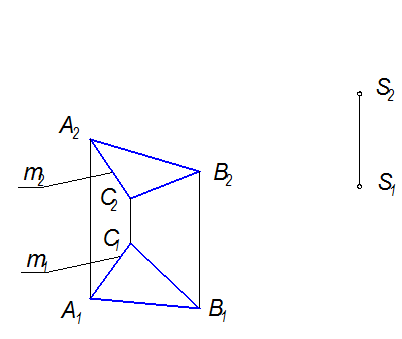
Рис. 2-44

2. Построить проекции поверхности (дискретный каркас) - это значит провести три образующие, соединив точки А,В,С с точкой S (рис.2-45).

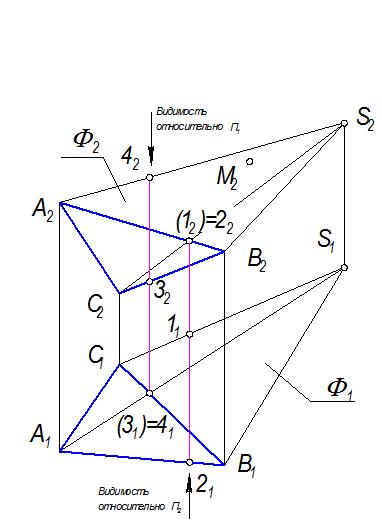
Рис. 2-45

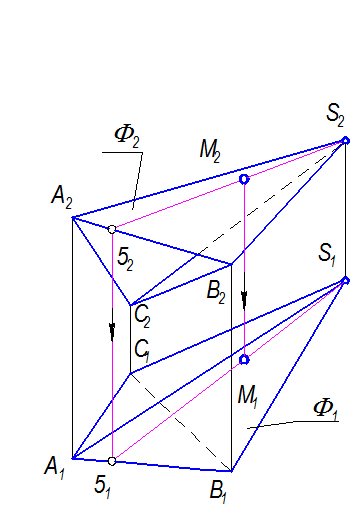
Рис. 2-46

3. Построить проекции линии обреза. В данном случае это- m (АВС)

4. Определить видимость поверхности (ребер и направляющей ломаной относительно друг друга методом конкурирующих точек).

Точки 1 и 2 - фронтально конкурирующие, определяют видимость относительно П₂.

Точки 3 и 4 - горизонтально конкурирующие, определяют видимость относительно П₁.

Часть С₂S₂ - видима, т.к. рассматриваем только боковую поверхность без основания

(рис. 2.46).

5. Точка М(М₂) принадлежит грани АВS(А₂В₂S₂). Чтобы построить М₁ (рис.2.41) нужно через точку М₂ провести какую - либо линию принадлежащую F (точнее, грани А₂В₂S₂), проще всего провести образующую 5₂S₂ Î М₂ , построить ее горизонтальную проекцию 5₁S₁ Þ М₁.

Точка М₁ - видима, т.к. на П₁ грань А₁В₁S₁ - видима.

Задача: сконструировать пирамидальную поверхность общего вида y, а(а₂) Ì y, а­₁ = ?

Определитель поверхности: y (АВDС, S), l Ç ABCD, l É S

1. Задать (построить) проекции элементов определителя.

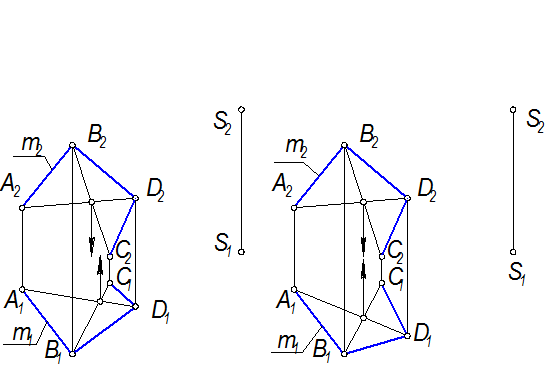
Рис. 2-47

Для удобства построения ломаную АВDС делаем плоской. Для этого проводим ее диагонали.

Поднимая или опуская одну из точек (D) , добиваемся того, чтобы m стала плоской

(рис. 2-47).

2. Построить проекции поверхности (дискретный каркас) - это значит провести четыре образующих (ребра).

3. Построить проекции линии обреза -сама направляющая является линией обреза: m(АВСD) (рис. 2-48)

4. Определить видимость поверхности.

а) Относительно П₂: точки 1 и 2 - фронтально конкурирующие.

б) Относительно П₁: точки 3 и 4 горизонтально конкурирующие.

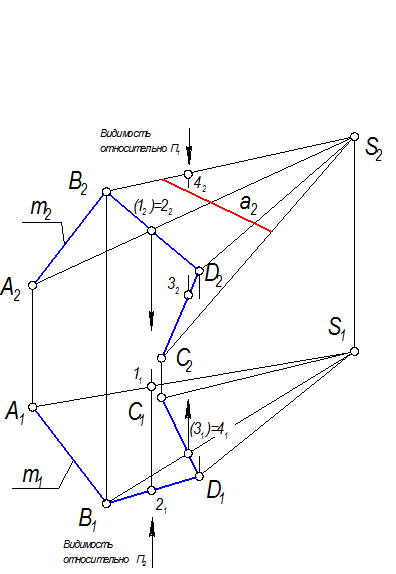
Рис. 2-48

5. а Ì y, а₂ É 5₂, 6₂, 7₂, 8₂ - точки строятся по принадлежности образующим (ребрам), следовательно а­₁ É 5₁, 6₁, 7₁, 8₁ (рис. 2-49).

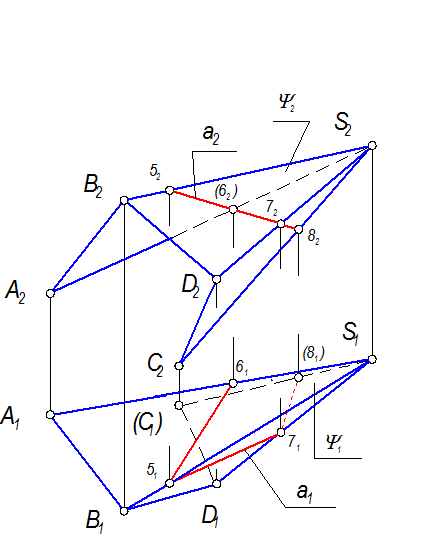
Рис. 2-49