Внешняя и внутренняя устойчивость графов.
Пусть G(x, Д) – ориентированный граф или неориентированный граф. Подмножество Д принадлежащее х называется доминирующим для G, если х\Д является подмножеством ГД, где ГД – отображение.
Теорема 1: Доминирующее множество Д0 является минимальным доминирующим множеством в том случае, когда для каждой вершины
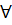 хi0
хi0 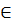 Д0
Д0
Выполняется одно из условий:
1) Вершине хi0 не существует входящего ребра (хj0 , хi0) внутреннего для
Д0 , оба конца которого лежат в Д0.
2) Существует ребро (хi0, хк), причём хi0 принадлежит, а хк принадлежит Х\Д0 единственное и идущее к хк.
Определение 1: Наименьшее число вершин составляет минимальное доминирующее множество и называется числом доминирования.
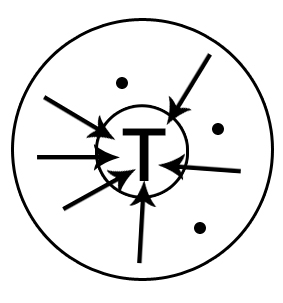
Определение 2: Подмножество Т множества Х называется внешним устойчивым множеством для графа Т, если разность Х\Т принадлежит
Т-1 * Т.
Таким образом все вершины, не принадлежащие множеству Т являются началом хотя бы одного ребра, ведущего в множество Т.
 Из определения 1 следует, что всё множество Т является внешне устойчивым.
Из определения 1 следует, что всё множество Т является внешне устойчивым.
Определение 3: Внешне устойчивое множество Т называется минимальным, не является внешне устойчивым.
В графе может быть несколько различных минимальных внешне устойчивых множеств с различным количеством вершин. Наименьшее число вершин, входящих в такое множество называется внешне устойчивым числом графа. 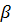 (G).
(G).
Из сравнения чисел любое доминирующее множество графа является внешне устойчивым, то есть для графа G(x) = G-1(x). В неориентированном графе понятия внешней устойчивости и доминирования совпадают.
Если G(x) неориентированный граф, то устойчивое число графа S(G) = 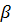 (G).
(G).
Для ориентированного графа такое равенство несправедливо.
Определение: Подмножество S входящее в Х называется внутренне устойчивым для графа G(x, Г), если пересечение S 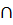 ГS =
ГS = 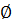 и ГS =
и ГS = 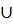 ГХ, Х принадлежит S. В частности следует, что пустое множество и множество S состоят из одной петли в единственной вершине.
ГХ, Х принадлежит S. В частности следует, что пустое множество и множество S состоят из одной петли в единственной вершине.
Внешне устойчивое множество является независимым и несвязным, если в некотором подмножестве вершин хотя бы одна пара соединена ребром, то такое подмножество является зависимым или внешне устойчивым.
Если в некотором подмножестве вершин любая пара вершин соединена ребром, то такое подмножество является полностью зависимым.
Независимое множество, которое становится зависимым после добавления одной вершины, называется максимально независимым множеством. Таким образом, в графе может существовать несколько независимых решений.
Максимальное число вершин, составляющее независимое множество называется числом независимости.
Теорема 2: Независимое множество в неориентированном графе максимально, когда оно доминирующее.
Необходимость: Предположим, что S максимальное множество, покажем, что оно доминирующее.
Для этого возьмем вершину хj принадлежащую Х\S.
S 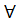 {xj} добавим ее к S. Множество S
{xj} добавим ее к S. Множество S 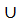 {xj} не будет независимым множеством так как вершина xj – конец ребра выходящего из S. Поэтому S – доминирующее.
{xj} не будет независимым множеством так как вершина xj – конец ребра выходящего из S. Поэтому S – доминирующее.
Достаточность: Предположим, S – неравно доминирующее множество. Покажем, что оно максимально. Для этого xj 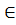 Х\S добавим к S
Х\S добавим к S 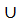 {xj}, ее добавление приводит к потере свойства, таким образом теорема 2 дает достаточное условие максимальной независимости графа.
{xj}, ее добавление приводит к потере свойства, таким образом теорема 2 дает достаточное условие максимальной независимости графа.
Из теоремы 2, 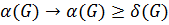 .
.
Дата добавления: 2016-06-05; просмотров: 4778;











