Лекция 25. Логарифмическая функция, ее свойства.
Логарифм по основанию a это функция 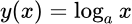 , обратная к показательной функции по основанию a: x(y) = a y.
, обратная к показательной функции по основанию a: x(y) = a y.
В дальнейшем будем считать, что основание логарифма a положительное, не равное единице число: 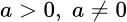 .
.
График логарифма
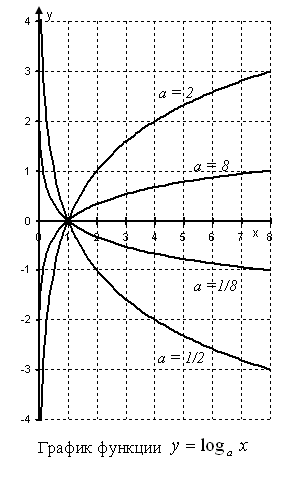 График логарифма получается из графика показательной функции зеркальным отражением относительно прямой y = x. На графике представлены значения логарифма
График логарифма получается из графика показательной функции зеркальным отражением относительно прямой y = x. На графике представлены значения логарифма
y(x) = loga x для четырех значений основания логарифма: a = 2, a = 8, a = 1/2 и a = 1/8. На графике видно, что при a > 1 логарифм монотонно возрастает. С увеличением x рост существенно замедляется. При 0 < a < 1 логарифм монотонно убывает.
Свойства логарифма
Область определения, множество значений, экстремумы, возрастание, убывание
Логарифм является монотонной функцией, поэтому экстремумов не имеет. Основные свойства логарифма представлены в таблице.
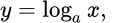 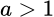
| 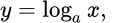 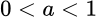
| |
| Область определения | 0 < x + ∞ | 0 < x + ∞ |
| Область значений | – ∞ < y < + ∞ | – ∞ < y < + ∞ |
| Монотонность | монотонно возрастающая | монотонно убывающая |
| Нули, y = 0 | x = 1 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | нет | нет |
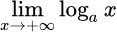
| + ∞ | – ∞ |
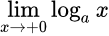
| – ∞ | + ∞ |
Частные значения
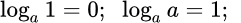
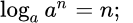
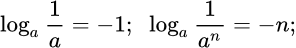
Логарифм по основанию 10 называется десятичным логарифмом и обозначается так:
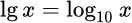
Логарифм по основанию e называется натуральным логарифмом:
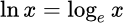
Натуральный логарифм это логарифм по основанию числа е: 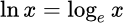 .
.
Десятичный логарифм это логарифм по основанию числа 10: 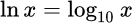 .
.
Основные формулы логарифмов
Свойства логарифма, вытекающие из определения обратной функции:
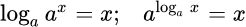
Основное свойство логарифмов и его следствия

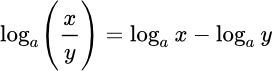
Дата добавления: 2016-06-05; просмотров: 2817;











