Лекция 24. Показательные функции, их свойства.
Показательная функция это функция y(x) = ax, зависящая от показателя степени x, при некотором фиксированном значении основании степени a.
Область определения показательной функции, множество значений
Рассмотрим показательную функцию y(x) = ax
В дальнейшем будем считать, что основание степени a является положительным числом: a > 0. Тогда функция y = ax определена для всех x. Ее область определения: - ∞ < x + ∞. При a ≠ 1 она имеет множество значений: 0 < y < + ∞ При a = 1 показательная функция является постоянной y = 1
График показательной функции
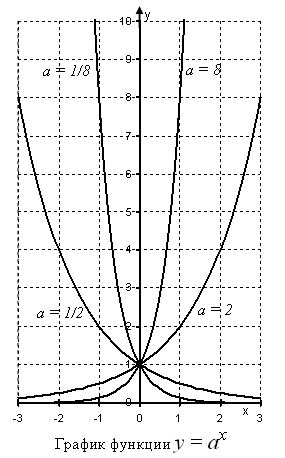 На графике представлены значения показательной функции
На графике представлены значения показательной функции
y(x) = ax
для четырех значений основания степени: a = 2, a = 8,a = 1/2 и a = 1/8. На графике видно, что при a > 1показательная функция монотонно возрастает. Чем больше основание степени a, тем более сильный рост. При 0 < a < 1 показательная функция монотонно убывает. Чем меньше показатель степени a, тем более сильное убывание.
Свойства показательной функции
Основные формулы
Когда показатель степени x есть натуральное число x = n, выражение an есть произведение n множителей:
| an = | a·a·a· ... ·a |
| n раз |
Для произвольного значения x показательная функция определяется так, что обладает всеми свойствами натурального показателя степени.
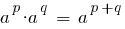
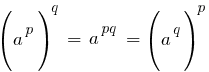
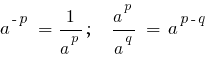
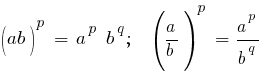
Частные значения
Пусть y(x) = ax. Тогда
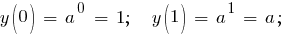
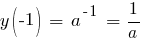
Экстремумы, возрастание, убывание
Показательная функция является монотонной, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице.
| y = ax, a > 1 | y = ax, 0 < a < 1 | |
| Область определения | - ∞ < x + ∞ | - ∞ < x + ∞ |
| Область значений | 0 < y < + ∞ | 0 < y < + ∞ |
| Монотонность | монотонно возрастающая | монотонно убывающая |
| Нули, y = 0 | нет | нет |
| Точки пересечения с осью ординат, x = 0 | y = 1 | y = 1 |
Дата добавления: 2016-06-05; просмотров: 2955;











