Лекция 23. Степенные функции, их свойства.

Свойства степенных функций и их графики

Степенная функция с показателем равным нулю, p = 0

Если показатель степенной функции y = x ^p равен нулю, p = 0, то степенная функция определена для всех x ≠ 0 и является постоянной, равной единице:
y = x ^p = x ⁰ = 1, x ≠ 0 .

Степенная функция с натуральным нечетным показателем, p = n = 1, 3, 5, ...

Рассмотрим степенную функцию y = x ^p = x ⁿ с натуральным нечетным показателем степени n = 1, 3, 5, .... Такой показатель также можно записать в виде: n = 2k + 1, гдеk = 0, 1, 2, 3, ... – целое не отрицательное. Ниже представлены свойства и графики таких функций.

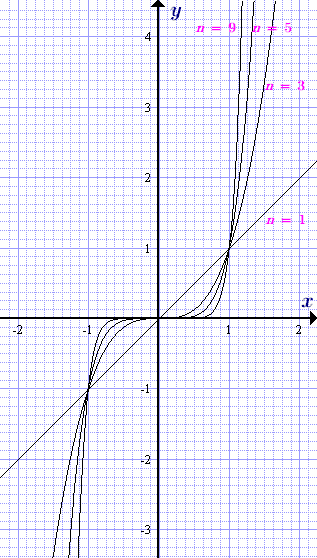
График степенной функции y = x ⁿ с натуральным нечетным показателем при различных значениях показателя степениn = 1, 3, 5, ....

Область определения: –∞ < x < ∞

Множество значений: –∞ < y < ∞

Четность: нечетная, y(–x) = – y(x)

Монотонность: монотонно возрастает

Экстремумы: нет

Выпуклость:

при –∞ < x < 0 выпукла вверх

при 0 < x < ∞ выпукла вниз

Точки перегибов: x = 0, y = 0

Точки пересечения с осями координат: x = 0, y = 0
Частные значения:

при x = –1, y(–1) = (–1) ⁿ ≡ (–1) ^2m+1 = –1

при x = 0, y(0) = 0 ⁿ = 0

при x = 1, y(1) = 1 ⁿ = 1

Степенная функция с натуральным четным показателем, p = n = 2, 4, 6, ...

Рассмотрим степенную функцию y = x ^p = x ⁿ с натуральным четным показателем степениn = 2, 4, 6, .... Такой показатель также можно записать в виде: n = 2k, где k = 1, 2, 3, ... – натуральное. Свойства и графики таких функций даны ниже.

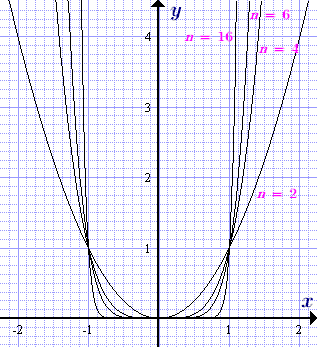
График степенной функции y = x ⁿ с натуральным четным показателем при различных значениях показателя степениn = 2, 4, 6, ....

Область определения: –∞ < x < ∞

Множество значений: 0 ≤ y < ∞

Четность: четная, y(–x) = y(x)

Монотонность:

при x < 0 монотонно убывает

при x > 0 монотонно возрастает

Экстремумы: минимум, x = 0, y = 0

Выпуклость: выпукла вниз

Точки перегибов: нет

Точки пересечения с осями координат: x = 0, y = 0
Частные значения:

при x = –1, y(–1) = (–1) ⁿ ≡ (–1) ^2m = 1

при x = 0, y(0) = 0 ⁿ = 0

при x = 1, y(1) = 1 ⁿ = 1

Степенная функция с целым отрицательным показателем, p = n = -1, -2, -3, ...

Рассмотрим степенную функцию y = x ^p = x ⁿ с целым отрицательным показателем степени n = -1, -2, -3, .... Если положить n = –k, где k = 1, 2, 3, ... – натуральное, то ее можно представить в виде:

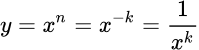
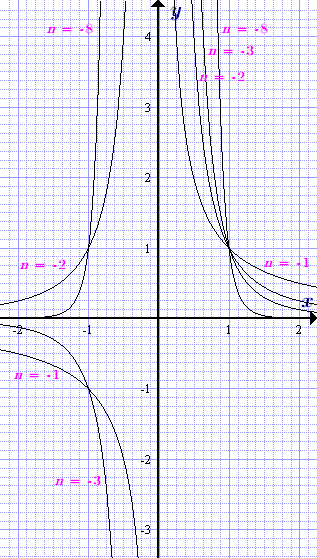
График степенной функции y = x ⁿ с целым отрицательным показателем при различных значениях показателя степени n = -1, -2, -3, ....

Нечетный показатель, n = -1, -3, -5, ...

Ниже представлены свойства функции y = x ⁿ с нечетным отрицательным показателем n = -1, -3, -5, ....

Область определения: x ≠ 0

Множество значений: y ≠ 0

Четность: нечетная, y(–x) = – y(x)

Монотонность: монотонно убывает

Экстремумы: нет

Выпуклость:

при x < 0: выпукла вверх

при x > 0: выпукла вниз

Точки перегибов: нет

Точки пересечения с осями координат: нет

Знак: при x < 0, y < 0

при x > 0, y > 0

Частные значения:

при x = –1, y(–1) = (–1) ⁿ = –1

при x = 1, y(1) = 1 ⁿ = 1

Четный показатель, n = -2, -4, -6, ...

Ниже представлены свойства функции y = x ⁿ с четным отрицательным показателем n = -2, -4, -6, ....

Область определения: x ≠ 0

Множество значений: y > 0

Четность: четная, y(–x) = y(x)

Монотонность:

при x < 0: монотонно возрастает

при x > 0: монотонно убывает

Экстремумы: нет

Выпуклость: выпукла вниз

Точки перегибов: нет

Точки пересечения с осями координат: нет

Знак: y > 0

Частные значения:

при x = –1, y(–1) = (–1) ⁿ = 1

при x = 1, y(1) = 1 ⁿ = 1

Степенная функция с рациональным (дробным) показателем

Рассмотрим степенную функцию y = x ^p с рациональным (дробным) показателем степени 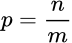, где n – целое, m > 1 – натуральное. Причем, n, m не имеют общих делителей.

Знаменатель дробного показателя - нечетный

Пусть знаменатель дробного показателя степени 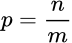нечетный: m = 3, 5, 7, ... . В этом случае, степенная функция x ^p определена как для положительных, так и для отрицательных значений аргумента. Рассмотрим свойства таких степенных функций, когда показатель pнаходится в определенных пределах.

Показатель p отрицательный, p < 0

Пусть рациональный показатель степени (с нечетным знаменателем m = 3, 5, 7, ... ) меньше нуля: .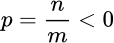

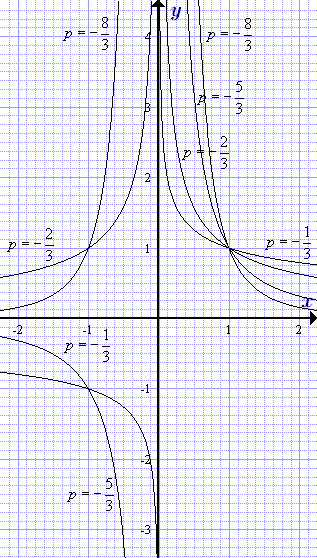
Графики степенных функций 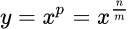с рациональным отрицательным показателем при различных значениях показателя степени 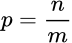, где m = 3, 5, 7, ... - нечетное.

Нечетный числитель, n = -1, -3, -5, ...

Приводим свойства степенной функции y = x ^p с рациональным отрицательным показателем 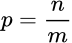, гдеn = -1, -3, -5, ... - нечетное отрицательное целое,m = 3, 5, 7 ... - нечетное натуральное.

Область определения: x ≠ 0

Множество значений: y ≠ 0

Четность: нечетная, y(–x) = – y(x)

Монотонность: монотонно убывает

Экстремумы: нет

Выпуклость:

при x < 0: выпукла вверх

при x > 0: выпукла вниз

Точки перегибов: нет

Точки пересечения с осями координат: нет

Знак:

при x < 0, y < 0

при x > 0, y > 0

Частные значения:

при x = –1, y(–1) = (–1) ⁿ = –1

при x = 1, y(1) = 1 ⁿ = 1

Четный числитель, n = -2, -4, -6, ...

Свойства степенной функции y = x ^p с рациональным отрицательным показателем 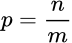, гдеn = -2, -4, -6, ... - четное отрицательное целое, m = 3, 5, 7 ... - нечетное натуральное.

Область определения: x ≠ 0

Множество значений: y > 0

Четность: четная, y(–x) = y(x)

Монотонность:

при x < 0: монотонно возрастает

при x > 0: монотонно убывает

Экстремумы: нет

Выпуклость: выпукла вниз

Точки перегибов: нет

Точки пересечения с осями координат: нет

Знак: y > 0

Показатель p положительный, меньше единицы, 0 < p < 1

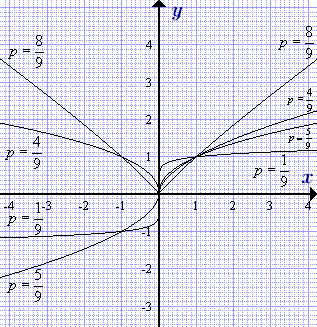
График степенной функции 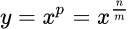с рациональным показателем (0 < p < 1) при различных значениях показателя степени 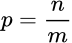, где m = 3, 5, 7, ... - нечетное.

Нечетный числитель, n = 1, 3, 5, ...

Представлены свойства степенной функции y = x ^p с рациональным показателем 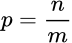, находящимся в пределах 0 < p < 1, где n = 1, 3, 5, ... - нечетное натуральное, m = 3, 5, 7 ... - нечетное натуральное.

Область определения: –∞ < x < +∞

Множество значений: –∞ < y < +∞

Четность: нечетная, y(–x) = – y(x)

Монотонность: монотонно возрастает

Экстремумы: нет

Выпуклость:

при x < 0: выпукла вниз

при x > 0: выпукла вверх

Точки перегибов: x = 0, y = 0

Точки пересечения с осями координат: x = 0, y = 0

Знак:

при x < 0, y < 0

при x > 0, y > 0

Частные значения:

при x = –1, y(–1) = –1

при x = 0, y(0) = 0

при x = 1, y(1) = 1

Четный числитель, n = 2, 4, 6, ...

Представлены свойства степенной функции y = x ^p с рациональным показателем 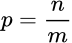, находящимся в пределах 0 < p < 1, где n = 2, 4, 6, ... - четное натуральное, m = 3, 5, 7 ... - нечетное натуральное.

Область определения: –∞ < x < +∞

Множество значений: 0 ≤ y < +∞

Четность: четная, y(–x) = y(x)

Монотонность:

при x < 0: монотонно убывает

при x > 0: монотонно возрастает

Экстремумы: минимум при x = 0, y = 0

Выпуклость: выпукла вверх при x ≠ 0

Точки перегибов: нет

Точки пересечения с осями координат: x = 0, y = 0

Знак: при x ≠ 0, y > 0