Настройка каналов регулирования для обеспечения заданных значений запасов устойчивости
Описанный в разделе 2.3.1 алгоритм приближенной настройки каналов ПИД-регулятора является теоретическим и не учитывает особенностей, порождаемых реальными условиями эксплуатации и технической реализации, в частности:
· конечный диапазон измерений физических переменных, например, ограниченная пропускная способность клапана;
· в ряде случаев отсутствует возможность изменения знака управляющего воздействия, например, реверсивный ход присутствует не во всех двигателях;
· ограниченная точность измерений, вследствие применения численных методов дифференцирования и интегрирования;
· наличие в системе или ее элементах типовых нелинейностей таких насыщение, гистерезис, люфт или ограничение;
· технологический разброс и случайные вариации значений параметров регулятора и объекта управления и т.д.
Процесс настройки ПИД-регулятора нефтехимических объектов управления по экспериментальным правилам интуитивен и попытки настроить регулятор без начального приближенного расчета коэффициентов (раздел 2.3.1) могут оказаться безуспешными. В результате аналитического обзора существующих методик [13, 34, 35] установлено, что методы Циглера-Никольса и Чина, Хронса, Ресвика наиболее приемлемы для промышленных условий.
Начальная приближенная настройка по формулам Циглера-Никольса обеспечивает повышенное значение настроечного коэффициента пропорционального канала регулирования, что упрощает процесс дальнейшей настройки. Зависимости для расчета каналов управления получены исходя из заданного значения декремента затухания ( 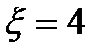 ), что приводит к длительному переходному процессу и дает возможность подстроить значение параметров. Методы Чина, Хронса и Ресвика обеспечивают больший запас устойчивости, чем метод Цинглера-Никольса, но с меньшим значением пропорционального коэффициента, следовательно, ухудшаются показатели точности управления.
), что приводит к длительному переходному процессу и дает возможность подстроить значение параметров. Методы Чина, Хронса и Ресвика обеспечивают больший запас устойчивости, чем метод Цинглера-Никольса, но с меньшим значением пропорционального коэффициента, следовательно, ухудшаются показатели точности управления.
Для обеспечения надежности регулятора, т.е. заданного значения запаса устойчивости, а также робастности системы управления, используются следующие методы:
· по распределению корней характеристического уравнения (критерий Е. Г. Дудникова) [11, 12];
· по виду импульсной переходной характеристики замкнутого контура (частотный показатель колебательности) [12];
· 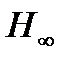 оптимизация и m анализ [10, 35];
оптимизация и m анализ [10, 35];
· ограничения на функцию чувствительности 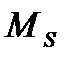 ,
, 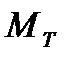 [13, 31];
[13, 31];
· анализ индекса робастности по передаточной функции замкнутой системы [13].
У каждого из перечисленных методов имеются достоинства и недостатки. В соответствии с поставленной задачей обеспечения надежности регулятора воспользуемся методом, основанном на анализе функции чувствительности 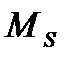 и комплементарной чувствительности
и комплементарной чувствительности 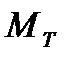 , рассчитываемых по амплитудно-фазовым характеристикам контура регулирования, что позволяет наглядно оценить процесс изменения запасов устойчивости и робастности системы.
, рассчитываемых по амплитудно-фазовым характеристикам контура регулирования, что позволяет наглядно оценить процесс изменения запасов устойчивости и робастности системы.
Передаточная функция реального объекта 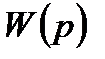 изменяется в процессе функционирования на некоторую величину
изменяется в процессе функционирования на некоторую величину 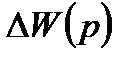 , например, вследствие изменения нагрузки на валу двигателя, старения или износа материала, появления люфта и т.д. Правильно спроектированная система автоматического управления должна сохранять свои показатели качества не только в идеальных условиях, но и в процессе эксплуатации в течение заданного промежутка времени (т.е. быть робастной). Для оценки влияния относительного изменения передаточной функции объекта
, например, вследствие изменения нагрузки на валу двигателя, старения или износа материала, появления люфта и т.д. Правильно спроектированная система автоматического управления должна сохранять свои показатели качества не только в идеальных условиях, но и в процессе эксплуатации в течение заданного промежутка времени (т.е. быть робастной). Для оценки влияния относительного изменения передаточной функции объекта 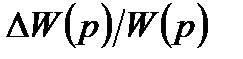 на передаточную функцию замкнутой системы
на передаточную функцию замкнутой системы 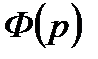 запишем выражение:
запишем выражение:
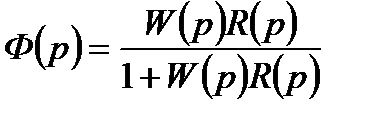 , (23)
, (23)
выделив передаточную функцию контроллера системы автоматического управления 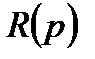 .
.
Вычислим производную передаточной функции замкнутой по передаточной функции объекта управления 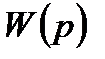 :
:
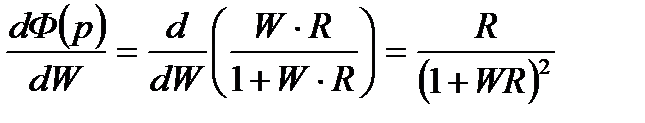 . (24)
. (24)
Не нарушая общности рассуждений, выразим из формулы (24) полный дифференциал передаточной функции замкнутой системы:
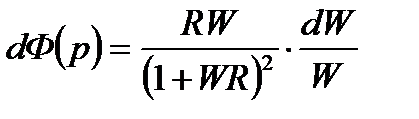 . (25)
. (25)
Подставив выражение (23) и разделив на 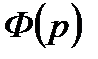 обе части равенства (25), получим зависимость:
обе части равенства (25), получим зависимость:
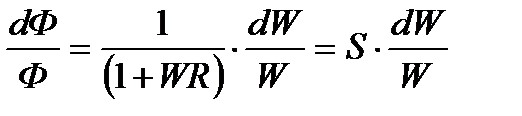 ,
,
где 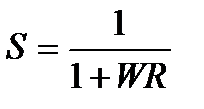 – это функция чувствительности или коэффициент, характеризующий влияние относительного изменения передаточной функции объекта управления на передаточную функцию контура регулирования.
– это функция чувствительности или коэффициент, характеризующий влияние относительного изменения передаточной функции объекта управления на передаточную функцию контура регулирования.
Комплементарной функцией чувствительности называется выражение вида:
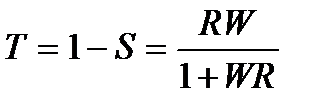 . (26)
. (26)
Поскольку обе функции являются частотно зависимыми, то анализ системы автоматического управления с их помощью целесообразно проводить с помощью частотных характеристик. Функции чувствительности позволяют оценить, как изменятся свойства системы после замыкания обратной связи:
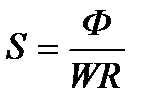 .
.
Если рассматривать передаточную функцию от входа возмущений d, то показатель будет рассчитываться следующим образом:
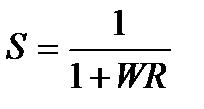 .
.
По виду функции 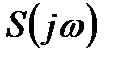 можно оценить, как изменяется процесс подавления внешних воздействий на систему на разных частотах после замыкания цепи обратной связи. Шумы, лежащие в диапазоне частот, соответствующем
можно оценить, как изменяется процесс подавления внешних воздействий на систему на разных частотах после замыкания цепи обратной связи. Шумы, лежащие в диапазоне частот, соответствующем 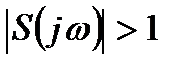 , будут усиливаться, а в интервале
, будут усиливаться, а в интервале 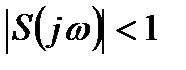 – ослабляться.
– ослабляться.
Наибольшее усиление внешних воздействий будет наблюдаться на частоте максимума модуля функции чувствительности:
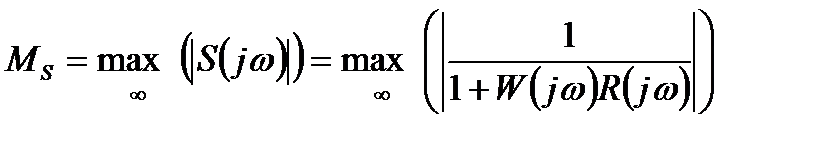 .
.
Максимум чувствительности связан с запасом устойчивости:
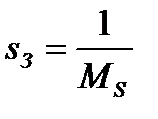
Оценка запаса устойчивости по усилению через максимум функции чувствительности запишется следующим образом:
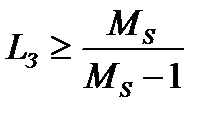 ;
;
Аналогично, но с более грубыми допущениями, определим оценку запаса по фазе через максимум функции чувствительности:
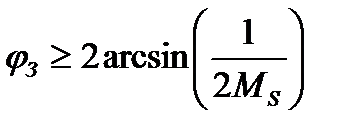 .
.
Робастность как способность системы сохранять заданный запас устойчивости при вариации ее параметров, вызванной изменением нагрузки, технологическим разбросом параметров, погрешностью модели и т.д. равнозначна низкой чувствительности запаса устойчивости к вариации параметров объекта.
В случае небольших интервалов изменения параметров, операцию дифференцирования передаточной функции с достаточной точностью можно заменить на процедуру вычисления конечной разности. В этом случае будет справедливым утверждение, что малым значениям модуля чувствительности соответствует небольшое влияние изменений параметров на передаточную функцию замкнутой системы и на запас устойчивости.
Для оценки больших изменений параметров объекта воспользуемся выражением:
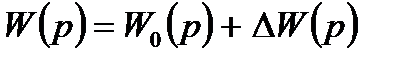 , (27)
, (27)
где 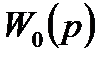 – расчетное значение передаточной функции, а
– расчетное значение передаточной функции, а 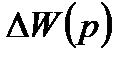 – величина отклонения, при которой система автоматического управления останется устойчивой.
– величина отклонения, при которой система автоматического управления останется устойчивой.
Умножив обе части выражения (27) на передаточную функцию 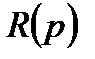 и используя в качестве запаса устойчивости для невозмущенной системы (до начала процессов, связанных с изменением параметров) расстояние до точки
и используя в качестве запаса устойчивости для невозмущенной системы (до начала процессов, связанных с изменением параметров) расстояние до точки 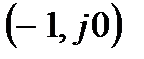 , условие устойчивости системы с отклонением петлевого усиления запишем следующим образом:
, условие устойчивости системы с отклонением петлевого усиления запишем следующим образом:
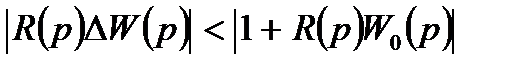
откуда
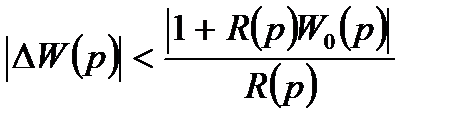 или
или 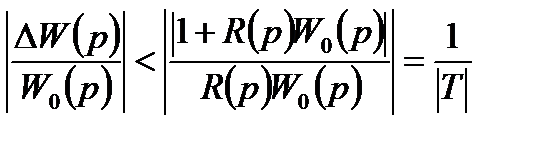 ,
,
где Т – дополнительная функция чувствительности, рассчитанная по формуле (26).
Проведем расчет настроек исследуемого технологического объекта управления в соответствии с описанной методикой, при этом передаточную функцию ПИД-регулятора запишем следующим образом:
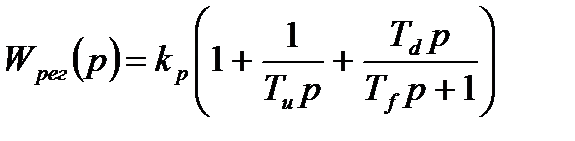 ,
,
где 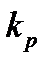 – пропорциональная часть,
– пропорциональная часть, 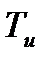 - постоянная интегрирования,
- постоянная интегрирования, 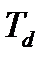 - постоянная дифференцирования,
- постоянная дифференцирования, 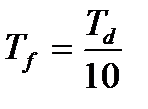 – постоянная фильтра.
– постоянная фильтра.
Частотная передаточная функция модели объекта управления, полученной в результате идентификации, запишется следующим образом:
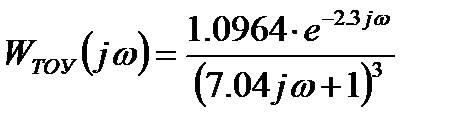 .
.
В качестве критерия качества переходного процесса воспользуемся интегральным показателем, который является компромиссным с точки зрения обеспечения требуемой точности управления и быстродействия системы. Интегральный критерий пропорционален 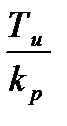 . Для обеспечения перерегулирования в диапазоне (5-10)% при постоянном значении постоянной дифференцирования
. Для обеспечения перерегулирования в диапазоне (5-10)% при постоянном значении постоянной дифференцирования 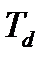 , увеличению
, увеличению 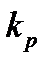 соответствует уменьшение
соответствует уменьшение 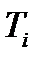 .
.
Дата добавления: 2021-05-28; просмотров: 702;











