Оценка вероятности события
Пусть нас интересует вероятность p некоторого события A и для её определения проведено n независимых, однородных испытаний. Пусть m(A) - число появлений события A при n испытаниях. Мы хотим понять, насколько хорошо относительная частота 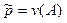 = m(A)/n оценивает p.
= m(A)/n оценивает p.
Поскольку 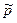 является случайной величиной и может отличаться от оцениваемого параметра, то возникает необходимость в оценке точности и надёжности найденного, то есть требуется знать, к каким ошибкам может привести замена неизвестного параметра его оценкой и с какой уверенностью можно ожидать, что ошибка не выйдет за известные пределы. С этой целью строится интервальная оценка, то есть по данным выборки указывается интервал, который с заданной и достаточно близкой к 1 вероятностью
является случайной величиной и может отличаться от оцениваемого параметра, то возникает необходимость в оценке точности и надёжности найденного, то есть требуется знать, к каким ошибкам может привести замена неизвестного параметра его оценкой и с какой уверенностью можно ожидать, что ошибка не выйдет за известные пределы. С этой целью строится интервальная оценка, то есть по данным выборки указывается интервал, который с заданной и достаточно близкой к 1 вероятностью 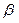 (её называют доверительной вероятностью или надёжностью оценки) накрывает неизвестный параметр.
(её называют доверительной вероятностью или надёжностью оценки) накрывает неизвестный параметр.
Рассмотрим отклонение относительной частоты n(А) от вероятности p , то есть разность 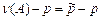 .
.
Воспользуемся тем, что по теореме Муавра-Лапласа величина 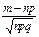 распределена приблизительно нормально и снова используем то, что для нормально распределенной величины x~N(0,1):
распределена приблизительно нормально и снова используем то, что для нормально распределенной величины x~N(0,1):
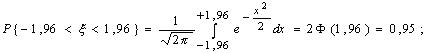
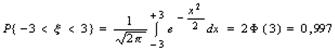 .
.
Следовательно
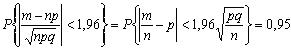 и
и
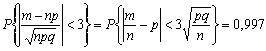 .
.
Мы определили выше числоkbкак корень уравнения 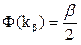 . Тогда с вероятностьюbвыполняется: неравенство
. Тогда с вероятностьюbвыполняется: неравенство
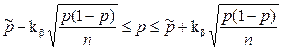 .
.
Полученная оценка справедлива при больших n и обладает тем недостатком, что зависит от p - неизвестной величины. От второго затруднения можно уйти, заменив в подкоренных выражениях p на 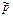 (вспомним, что
(вспомним, что 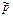 сходится по вероятности к p, что дает
сходится по вероятности к p, что дает
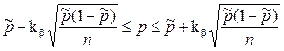 . (2.28)
. (2.28)
Что касается величины n, то практически удовлетворительный результат получается при npq > 9 .
Интервал, задаваемой формулой (2.28) и накрывающий параметр с вероятностью b, называется доверительным, b- это доверительная вероятность или уровень доверия, а a = 1-b – вероятность ошибки.
Пример . Из подвергнутых испытаниям на сортность 100 единиц товара из большой партии 80 выдержали его. Найти интервальную оценку для вероятности того, что произвольно выбранный образец является высокосортным, при условии, что оценка окажется неправильной не более, чем в 5% случаев.
Решение. В качестве точечной оценки неизвестного параметра принимаем 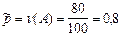 . По доверительной вероятности b=0,95 с помощью таблицы значений функции Лапласа находим kb= 1,96 и затем по формуле (2.28) определяем двусторонний доверительный интервал:
. По доверительной вероятности b=0,95 с помощью таблицы значений функции Лапласа находим kb= 1,96 и затем по формуле (2.28) определяем двусторонний доверительный интервал:
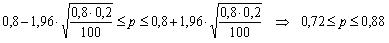
- с гарантией 0,95 доля высокосортного товара партии составляет от 72% до 88%.
Дата добавления: 2017-01-08; просмотров: 3801;










