Разностные уравнения

В настоящее время никто не сомневается в том, что математические методы наряду с физическими и химическими являются мощным инструментом при исследовании чисто биологических проблем. С помощью математического аппарата можно описать динамику биологических систем. Для определенности биологической переменной в большинстве случаев обычно служит численность некоторого вида в данной среде как функция времени.

Можно построить как дискретные, так и непрерывные модели процессов, зависящих от времени. В дискретных моделях время представляет собой дискретную переменную, и наблюдения выполняются лишь через определенные дискретные интервалы времени. В непрерывной модели время представляет собой непрерывную переменную, и численность популяции остается непрерывно изменяющейся во времени.

В дискретных моделях популяционного роста величина 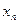обозначает численность популяции к концу n-го периода времени. По окончании одного периода времени численность равна 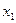; по окончании двух периодов она равна 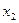и т.д. развитие популяции во времени описывается последовательностью чисел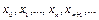

Определение 1.1. Разностным уравнениемназывается уравнение, которое связывает между собой значение 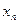при различных значениях индекса n. Если 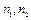представляют собой наибольший и наименьший из индексов n, встречающихся в записи уравнения, то порядок разностного уравнения есть .

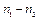Пример 1.1. Уравнение 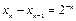– уравнение первого порядка; 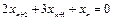– уравнение второго порядка; 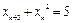– уравнение третьего порядка.

Пример 1.2. Популяция насекомых увеличивается таким образом, что прирост за n-й период времени вдвое больше прироста за предыдущий период времени. Требуется описать этот процесс роста с помощью разностного уравнения. Каков порядок этого уравнения?

Решение. Пусть 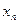– численность популяции после n периодов времени. Тогда прирост за n-й период выражается величиной 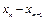, а прирост за (n – 1)-й период – величиной 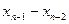. По условиям задачи имеем:

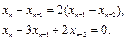
Это разностное уравнение второго порядка.

Пример 1.3. Крупный рогатый скот выкармливается с целью максимизировать живую массу к моменту убоя. Масса средней коровы за каждую неделю возрастает на 5 %. Требуется описать этот процесс с помощью разностного уравнения. Каков порядок этого уравнения?

Решение. Пусть 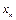– масса средней коровы после n недель. После n+1недель величина 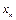увеличивается на 5 %. Отсюда получаем 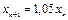. Это разностное уравнение первого порядка.