Понятие случайного сигнала (СС) и применение для его описания законов распределения и неслучайных числовых характеристик закона распределения.
Колебание Х(t) называется случайным сигналом, если его значения в любой момент времени являются случайными величинами Х(ti).
Хi=Х(ti) – одномерная случайная величина
Если генератор случайного колебания включить на время Т и записать результат х(t), то этот результат принято называть– реализацией СС.
Реализация СС – это детерминированный сигнал.
Если многократно повторить этот эксперимент, то получится ансамбль реализаций { хк(t) }.
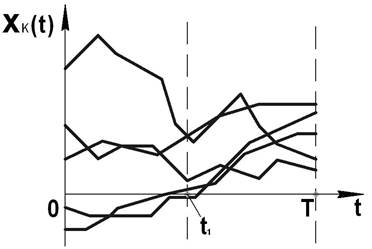
Случайную величину 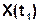 можно назвать сечением случайного сигнала
можно назвать сечением случайного сигнала 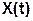 в момент времени
в момент времени 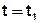 .
.
Полное статистическое (вероятностное) описание одномерной случайной величины (СВ) Х(t1) дает одномерный закон распределения СВ.
Имеются две разновидности одномерного закона распределения.
1) Интегральный закон распределения (функция распределения)
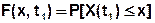 - вероятность того, что СВ не превышает некоторого значения х.
- вероятность того, что СВ не превышает некоторого значения х.
Значения функции распределения можно найти по ансамблю реализаций:
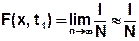 (при больших N)
(при больших N)
N – полное число реализаций
l – число реализаций, удовлетворяющих условию Х(t1)≤x
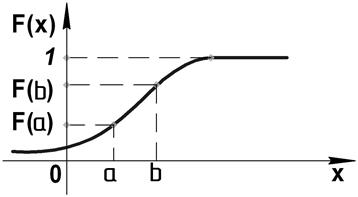
Свойства функции распределения:
- безразмерная.
- неубывающая.
- 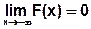
- 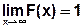
- 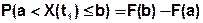
2) Дифференциальный закон распределения (плотность вероятности).
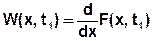
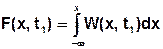
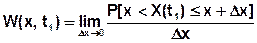
Свойства плотности вероятности:
- размерность [1/x]
- W(x)≥0
- свойство нормировки 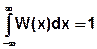
- 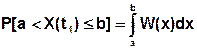
Пример:
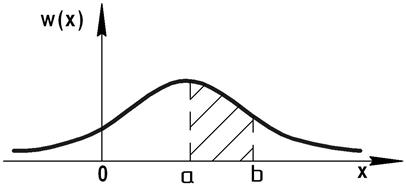
Заштрихованная площадь характеризует вероятность попадания СВ в интервал от a до b.
В общем случае одномерный закон распределения зависит от того, в какой точке проведено сечение, т.е. одномерный закон распределения – функция времени.
Кроме одномерного закона распределения для описания случайных величин можно использовать неслучайные числовые характеристики одномерного закона распределения (моменты распределения).
Неслучайные числовые характеристики делятся на:
1) Начальные моменты распределения.
- начальный момент первого порядка (математическое ожидание СВ) – это среднее значение СВ. Усреднение проводиться по ансамблю реализаций и обозначается 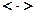 .
.
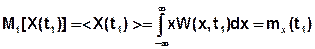
- начальный момент второго порядка – это среднее значение квадрата СВ.
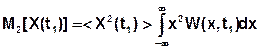
- начальный момент k-порядка – среднее значение СВ в степени k.
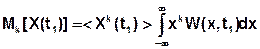
2) Центральные моменты распределения – начальные моменты от центрированной СВ:
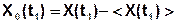
Второй центральный момент
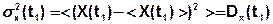
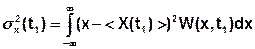
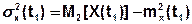
В общем случае неслучайные числовые характеристики зависят от момента времени, в который проведено сечение, т.е.
mx(t), 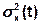 - функции времени.
- функции времени.
Знание одномерных законов распределения в различных сечениях СС не дает полного описания СС даже если число сечений стремится к бесконечности, так как одномерный закон распределения не содержит информации о взаимосвязи значений СВ в разных сечениях.
Для более полного описания СС необходимо рассматривать совокупность сечений СС как n-мерную случайную величину {X1,X2,…,Xn}. Для описания n-мерной случайной величины применяют n-мерный закон распределения.
W(x1 x2, …xn) – n-мерная плотность вероятности.
Свойства n-мерной плотности.
- нормировка
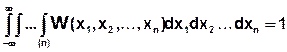
- зная n-мерную плотность можно найти одномерную плотность в любом сечении
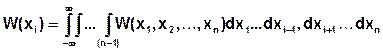
- статистическая независимость сечений. Два сечения называются статистически независимыми, если двумерная плотность равна произведению одномерных плотностей.
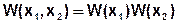
Если все сечения статически независимы, то
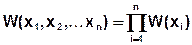
Заметим, что n-мерный закон распределения дает полное статистическое описание СС при n→∞.
Дата добавления: 2021-04-21; просмотров: 448;











